Однією з важливих характеристик якісної системи автоматичного керу-вання (САК) є її точність в усталених режимах. Забезпечення астатизму системи за навантаженням сприяє підвищенню
продуктивності роботи механізму і підвищує ефективність застосування САК. В той же час організація регулювання будь-якої координати за принципом негативного зворотного зв’язку вважає за необхідне вимірювання
або оцінку відповідної величини з достатньою точністю.
В теперішній час теорія синтезу спостерігачів стану (СС) лінійних стаціонарних систем розроблена достатньо широко, що дало можливість для їхнього впровадження у промислові системи електропривода (ЕП) постійного
струму. Серед лінійних СС з позиції викладеного слід окремо виділити СС, які дозволяють встановлювати сигнал динамічного струму (моменту), який не можна вимірити безпосередньо, з метою забезпечення астатизму САК
за обуренням (статичним навантаженням) без зайвого підвищення її інерційності [1]. Ця ідея може бути застосована і до ЕП змінного струму, причому однією з областей перспективного впровадження лінійних СС є системи
частотно-регульованого ЕП зі скалярним керуванням, які за умов існуючих задовільних динамічних властивостей можуть потребувати підвищення точності роботи системи в усталених режимах. Вирішенню вказаної
науково-технічної задачі і присвячена ця стаття.
Метою даної роботи є оцінка можливості синтезу лінійних СС для систем частотно-регульованого асинхронного ЕП.
Для цього вирішуються такі задачі:
встановлення областей практичного використання розроблених СС.
Вихідна модель АД та її лінеаризація. За умови прийняття традиційних допущень рівняння рівноваги напруг статора та ротора короткозамкненого АД у синхронній ортогональній сис-темі координат x,y ,
орієнтованій за вектором напруги статора:

до яких входять складові iSx,iSy, струму та ΨSx, ΨSy , потокозчеплення ста-тора, мають вигляд:

де p=d/dt – оператор диференціювання; α=RR/LR – коефіцієнт згасання ротора;RS , RR – активні опори обмоток фаз статора і приведений ротора від-повідно;
LS, LR – повні індуктивності статора і ротора відповідно; σ – коефіцієнт розсіювання; Lm – взаємоіндуктивність; ώs – кутова частота напруги
статора (частота обертання системи координат x,y ); ώR – кутова частота обертання ротора, приведена до кількості пар полюсів Zp статора.
Рівняння електромагнітного моменту відповідно до обраної структури моделі АД:
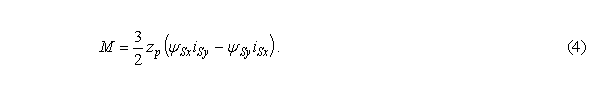
Рівняння руху ЕП на основі двигуна, ротор якого обертається, має ви-гляд:

де J , MC – сумарні момент інерції системи „двигун – механізм” і сумарний момент статичного навантаження, приведені до валу АД, відповідно.Математичну модель АД, складену з рівнянь (2) – (5), будемо
вважати такою, що досить точно відповідає досліджуваному об’єктові, і стосовно неї в подальшому застосовуємо назву вихідна модель АД.Перетворення (2) – (4) з урахуванням додаткових припущень про малу величину
активного опору статора та про малий вплив ЕРС обертання АД дають рівняння:
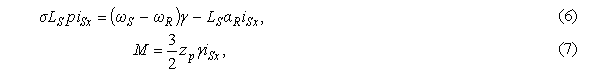
де співвідношення γ =US/ώS чисельно дорівнює амплітуді вектора потокозчеплення статора за умови зневажання активним опором статора АД, і може визначатися обраним законом частотного керування.
Рівнянням (5) – (7) відповідає так звана лінеаризована модель АД. Значення параметру γ в лінеаризованій моделі доцільно обрати рівним співвідношенню номінальних значень амплітуди і частоти напруги статора:

Відомо, що залежності, які можуть бути отримані за допомогою лінеаризованої моделі, при роботі АД на робочій ділянці лінійної частини механічних характеристик мають досить високу збіжність із залежностями,
отриманими за допомогою вихідної моделі АД (похибка по швидкості зазвичай не перевищує припустимих меж). Саме тому лінеаризовану модель традиційно використовують при дослідженні замкнених САК швидкістю асинхронних ЕП.
З іншого боку, оскільки лінеаризована модель АД достатньо точно імітує поведінку об’єкта на робочій частині механічних характеристик, то вона може бути застосована для синтезу СС при їх подальшому використанні у системах ЕП,
робота яких відповідає умові лінеаризації.
Представимо перетворювач частоти (ПЧ) в колі статора спрощено аперіодичною ланкою, розташованою у каналі завдання частоти АД, з малою сталою часу Tµ і коефіцієнтом підсилення kµ , який дорівнює
відповідному коефіцієнту передачі ПЧ. В результаті можна отримати структурну схему ОС, яка представлена на рис.1, де TR=1/αR – електромагнітна стала часу кола ротора АД.
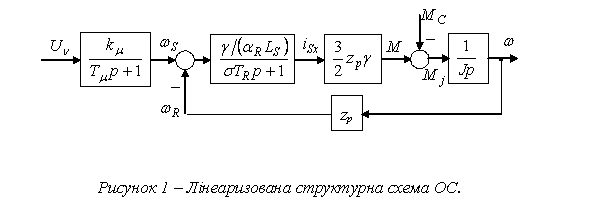
Синтез спостерігачів стану.
На основі структурної схеми ОС (рис.1) згідно з [2] були синтезовані СС повного порядку із організацією корегуючого зворотного зв’язку за різницею виміреної і оціненої швидкостей (рис.2). Спостерігачі належать до класу СС
повного порядку і відрізняються один від одного порядком частини ОС (рис.1), яка оцінювалась.
За умови обрання у якості бажаних поліномів Баттерворта вирази для корегувальних коефіцієнтів СС мають вигляд:


Оцінка точності встановлювання СС динамічного моменту.
Дослідимо роботу синтезованих СС при роботі АД у типових штатних режимах на прикладі двигуна МТК-52-8 (28 кВт, 380 В, 50 Гц). Для отримання дійсної величини динамічного моменту АД застосовуємо вихідну модель двигуна, а
оцінені значення динамічного моменту АД отримуємо зі СС. Обрані чисельні значення: Tµ=3мс, Ω0=1/Tµ.
На рис. 3, 4 представлені графіки сигналу дійсного і оцінених ( 1, 2, 3) за допомогою синтезованих СС відповідного порядку (рис.2) сигналів динамічного моменту АД. Чисельні значення динамічного моменту подані у долях
номінального електромагнітного моменту АД, час – у кратності до величини еквівалентної сталої часу ПЧ Tµ.
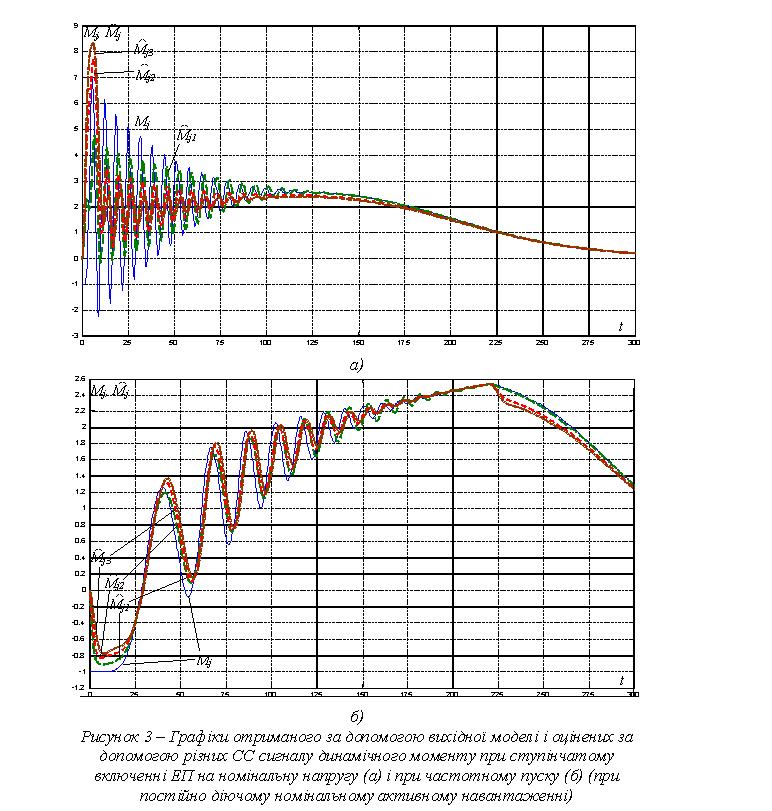
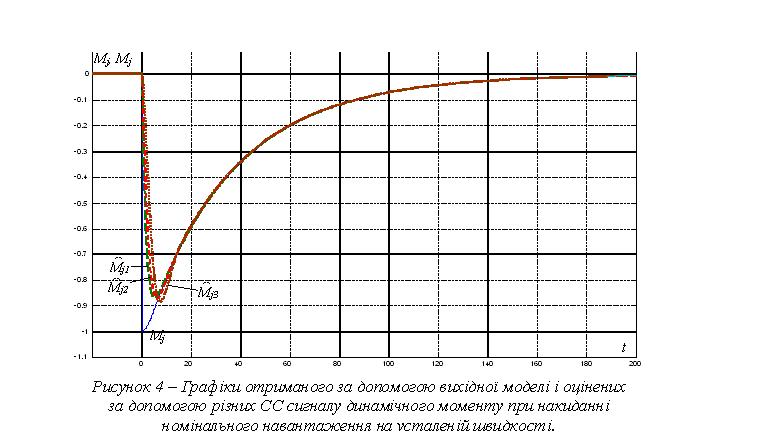
Аналіз графіків показує, що в режимі прямого пуску (коли ковзання АД близьке до одиниці) (рис.3а) найбільшу точність оцінювання середнього значення динамічного моменту АД забезпечує СС першого порядку. Спостерігачі
другого та третього порядку дають занижене значення оцінки динамічного моменту при великих ковзаннях, що обумовлено розбіжністю в описі електромагнітних контурів АД за допомогою лінеаризованої та вихідної моделей.
При малих ковзаннях, як видно також і з графіків рис. 3б, 4, похибка оцінювання відсутня повністю за умови згасання електромагнітного перехідного процесу.
Таким чином, синтезовані СС з достатньою точністю дозволяють встановити значення динамічного моменту АД у всіх штатних режимах, що дозволяє організовувати зворотні зв’язки за цією величиною.
Встановлення областей практичного використання розроблених СС.
Оскільки СС синтезовані на основі лінеаризованої моделі АД, яка є об-меженою з позиції можливості отримання вичерпної інформації про стан об’єкта, то і самим спостерігачам властиві відповідні недоліки. Так, синтезо-вані СС
не дозволяють оцінювати значення складових струму статора в ортогональній системі координат, а також встановлювати значення потокозчеплення статора з достатнім ступенем точності, що робить їх непридатними для застосування
у системах асинхронного ЕП з векторним керуванням.
Але отримані результати досліджень показують, що розроблені СС можуть бути застосовані до систем асинхронного ЕП зі скалярним частотним керуванням, і відкриває перспективи щодо їхнього вдосконалення: в такому випадку
астатизм системи ЕП за навантаженням може бути забезпечений шляхом заміни регулювання струму статора АД організацією регулювання динамічного моменту двигуна.
Серед синтезованих СС лише спостерігач третього порядку (рис.2в) може бути реалізований у чистому вигляді (тобто, без застосування додаткових пристроїв), оскільки сигнал завдання на частоту напруги АД може бути
безпосередньо заведений із САК. Застосування СС першого порядку потребує вирішення питання оцінки складової струму статора iSx з урахуванням умови орієнтації (1), а СС другого порядку – побудування пристрою оцінки
частоти основної гармоніки фактично несинусоїдальної періодичної напруги на затискачах АД, що не є доцільним.
Висновки.
Таким чином, в даній роботі показано, що лінійні СС, які синтезуються на основі лінеаризованої моделі об’єкту “ПЧ – АД”, можуть бути застосовані для достатньо точного встановлення окремих параметрів реально нелінійного ОС. Синтезовані СС першого, другого та третього порядків достатньо точно встановлюють значення динамічного моменту АД як в усталених, так і в перехідних режимах, і можуть бути рекомендовані до застосування у замкнених системах, які забезпечують досить плавну зміну керуючого сигналу, з метою забезпечення астатизму за навантаженням і підвищення точності регулювання.
Найбільша точність оцінювання динамічного моменту властива СС першого порядку, як найбільш наближеному до реального об’єкту, а найбільша простота реалізації САК буде мати місце при застосуванні СС третього порядку. Реалізація системи асинхронного частотно-регульованого ЕП зі СС другого порядку практично є неможливою.
Подальші дослідження в цій області будуть спрямовані на питаннях по-будування системи ЕП зі зворотним зв’язком за оцінкою динамічного моменту, реалізації СС і системи в цілому, її синтезі і налагодженні.
Литература
- Система подчиненного регулирования скорости с обратной связью по оценке динамического тока / Коцегуб П.Х., Толочко О.И., Мариничев В.Ю., Никорюк Н.С., Розкаряка П.И. // Збірник наукових праць ДонНТУ. Серія “Електротехніка
і енергетика”. – Випуск 28. – Донецьк:
ДонНТУ, 2001. – С. 18 – 26.
- Толочко О.І. Аналіз та синтез електромеханічних систем зі спостерігачами стану: Навч. посібник. – Донецьк: Норд-Прес, 2004. – 298 с.