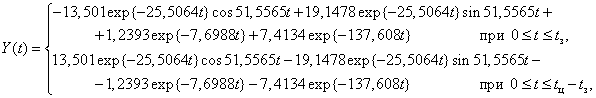В стандартах [1, 2] на електромагнітну сумісність (ЕМС) нормуються допустимі розмахи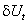 
коливань напруги 
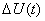в 
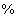у функції їх частоти 
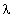у Гц. Проте розглядаються лише коливання у формі меандру, хоча їх вплив залежить і від коефіцієнта заповнення 
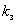. Окрім кривих коливань нормується доза флікера (ДФ) 
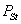, яка є універсальним показником ЕМС. Розрахунки доз виконуються чисельними методами, починаючи з нульових начальних умов. При цьому немає можливості контролювати похибку, яка може накопичуватися від циклу до циклу.
В статті пропонується аналітичний розв’язок задачі про ДФ при прямокутних коливаннях, що дозволяє отримати допустимі криві коливань з різними 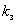, а не тільки 
.
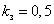Флікермодель з [2] включає до себе зважувальний фільтр (ФЗ), блок квадратичного інерційного згладжування (КІЗ) і блок визначення ДФ. ФЗ моделює лампу і реакцію Y(t) мозку людини на коливання освітлення. Блок КІЗ моделює зорове відчуття S(t) , яке пов’язано з додатковою втомою людини.
Реакція ФЗ повинна визначатися розв’язком диференційного рівняння четвертого порядку. З цією метою застосуємо метод парціальних реакцій (ПР) [3], згідно з яким ФЗ представляється у вигляді чотирьох паралельно з’єднаних інерційних ланок. Для визначення їх параметрів знайдемо полюса передавальної функції ФЗ: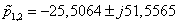 
, 
, 
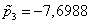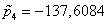1/с, що дозволяє знайти коефіцієнти передачі: 
, 
, 
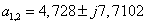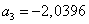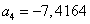та частоти зрізу 
, 
, 
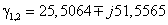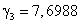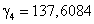, де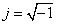 
. Парціальні реакції інерційних ланок є відомими, тому шукана реакція дорівнює сумі ПР.
Знайдемо періодичний розв’язок щодо реакції ФЗ на прямокутне коливання. Початкова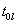 
і кінцева 
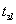ординати кожної l-ої ПР розраховуються за формулами: 
, 
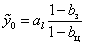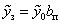,де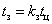 
, 
, 
, 
.
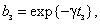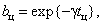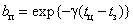На першій ділянці ПР змінюється від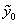 
до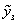 
, а на другій – від 
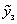до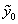 
. Реакції визначаються формулами (2.57) з [4]. Підсумовування ПР дає кінцевий вираз:
Після визначення реакції ФЗ, вона підноситься до квадрату і пропускається крізь інерційну ланку зі сталою часу 0,3 с , тобто через блок КІЗ. Визначенням ДФ за процедурою, яка описана в [1, 2], була знайдена залежність ДФ від розмаху і частоти коливань. Підставивши в неї допустиме значення ДФ, яке дорівнює одиниці, знайдемо криві допустимих коливань функції частоти (рис.1). Крива коливань з [2] співпадає з розрахованою кривою при kз = 0,5. Як видно, у зоні частот нижче за 3 Гц допустимі коливання майже не залежать від коефіцієнту заповнення. При більших частотах коливання тим менше діють на людину, чим меншим є коефіцієнт заповнення. У цих випадах використання кривих зі стандартів дає значне завищення оцінок ЕМС.
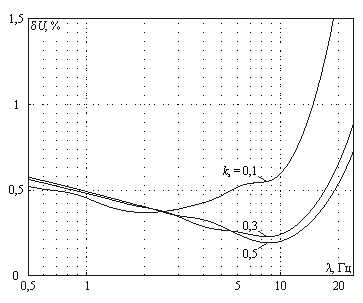
Рисунок 1 – Криві допустимих коливань у функції частоти
Таким чином, отриманий аналітичний розв’язок задачі щодо ДФ прямокутних коливань дозволяє удосконалити норми [1, 2] шляхом введення до цих стандартів кривих з рис.1.Перелік посилань
1. ГОСТ 13109-97. Межгосударственный стандарт. Электрическая энергия. Совместимость технических средств электромагнитная. Нормы качества электрической энергии в системах электроснабжения общего назначения. – Введ. в Украине с 01.01.2000.2. CEI/IEC 61000-4-15. Electromagnetic compatibility – Part 4, Section 15: Flickermeter – Functional and design specification. 1997.
3. Куренный Э.Г., Лютый А.П., Черникова Л.В. Метод парциальных реакций для анализа процессов на выходе линейных фильтров в моделях электромагнитной совместимости. – Электричество, 2006, №10. – С.11-18.
4. Кузнецов В.Г., Куренный Э.Г., Лютый А.П. Электромагнитная совместимость. Несимметрия и несинусоидальность напряжения. – Донецк: Норд-Пресс, 2005. – 250 с.