Источник: http://zdd.1september.ru/articlef.php?ID=200502202
Норма в обществе – это то, что «принято» (законом, большинством, традицией и т.п.). Когда речь идет о свойствах организма, природная и общественная нормы могут порой и не совпадать. Однако это – довольно редкое явление, обычно нормы в обществе устанавливаются на основе того, что естественно и «нормально» в природе.
Математический закон, который отражает такие правила, назвали не только по имени авторов, но еще и нормальным законом распределения. По-латыни «норма» означает «правило». Любой признак, частота встречаемости которого соответствует закону Гаусса–Лапласа, называют нормально распределенным.
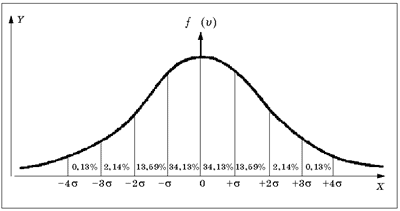
В качестве примера рассмотрим такой параметр, как рост человека. На рис. 1 по горизонтальной оси – линейка с показателями длины тела, а по вертикали отложены числа, указывающие, сколько раз такая длина тела встретилась при измерении роста, допустим, тысячи человек одного пола и возраста. И получается при этом ровный такой колокол, внутри которого поместилась вся тысяча человек. Колокол не просто ровный, он совершенно симметричный, и середина линейки соответствует самой высокой точке колокола. Это означает, что чаще всех встречаются люди именно с такой длиной тела. И очень часто встречаются люди с ростом немного меньше или немного больше.

Рисунок 1 – Кривая закона нормального распределения
Важное свойство закона Гаусса–Лапласа состоит в том, что построение упомянутого выше колокола основано на двух математических показателях – параметрах нормального закона распределения. Один из них – среднее арифметическое значение, т.е. мера «положения» этого колокола. Чтобы найти это число, надо сложить рост тысячи человек и сумму эту на тысячу разделить. Среднее значение одновременно оказывается серединой нашей линейки. Более того, напротив этой точки находится самая высокая точка колокола – значит, самый часто встречающийся рост. Эта же точка на оси разделяет ровно пополам количество всех встречаемых прохожих – тех, кто ростом ниже среднего, и тех, кто выше.
Второй параметр закона Гаусса–Лапласа называется стандартным отклонением, потому что он характеризует меру случайных отклонений, или «колебаний», измеряемого признака относительно среднего значения – ведь значение признака (роста, в частности) от человека к человеку колеблется, варьируется, потому что мы измеряем рост у случайных людей, лишь бы они были взрослыми мужчинами одного возраста.
На тех же принципах основаны и самые разные системы оценки, предназначенные для определения уровня достижений человека. Пользуются ими антропологи, гигиенисты, специалисты по физическому воспитанию, социологи и другие ученые, работающие в области наук о человеке. Используется для этого такая же «линейка», только деления на ней соответствуют не сантиметрам длины тела, а тем единицам, в которых измеряется интересующий нас показатель. И на эту линейку наносится шкала оценок. Каждой оценке – свой диапазон значений в долях сигмы. Поэтому такие шкалы оценок называют сигмальными.
Поскольку при построении шкалы на линейку значений оцениваемого признака наносятся границы, рассчитанные с помощью параметров нормального распределения, то и пользоваться ими можно только в тех случаях, когда точно известно, что этот закон соблюдается. Но если хорошего «колокола» не получается (например, все значения признака встречаются одинаково часто) или же колокол очень неровный либо несимметричный, то использовать такую шкалу неправильно с точки зрения математики, а стало быть, и здравого смысла, потому что принятые параметры верны только для нормального закона распределения. Если закон распределения иной, то и правила расчетов нужно использовать иные, для такого случая разработанные.
Вот и возникают вопросы: когда все же можно пользоваться такой шкалой, а когда нет? Если нельзя, то почему и как тогда надо поступать? И особенно важный вопрос: как быть с детьми, которые хотя и в одном классе учатся, а такие разные? Ответы на все эти вопросы основаны на четком соблюдении правил математической статистики.