Оценка инновационного потенциала предприятия методом Саати

Коваленко Е.В., Евдокимов Ф.И.

Донецкий национальный технический университет

Источник: Всеукраинская научно-практическая конференция студентов и молодых учёных. "Современное состояние и проблемы инвестиционного развития". - Донецк - 2009, с. 45-46.

   Первым этапом применения МАИ является структурирование проблемы выбора в виде иерархии или сети. В наиболее элементарном виде иерархия строится с вершины (цели), через прмежуточные уровни-критерии (технико-экономические параметры) к самому нижнему уровню, который в общем виде случае является набором альтернатив (хостинг-провайдеров в нашем случае). Например, 3 шахты имеют разный потенциал, по разному развиты технческие, кадровые, финансовые и другие ресурсы. Рассмотрим факторы, влияющие на инновационный потенциал предприятия. Разобъём инновационный потенциал на четыре составляющие: интеллектуальные, информационные, финансовые и кадровые ресурсы. Эти критерии разобъём на три варианта: случай 1, случай 2, случай 3. Задача заключается в том, чтобы выбрать наиболее приемлимый вариант.

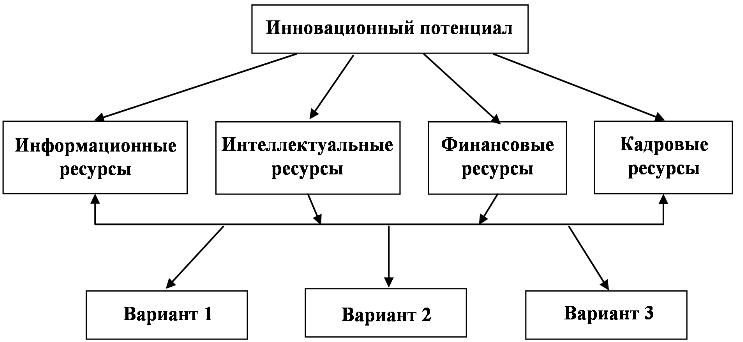
Рисунок. Декомпозиция задачи в иерархию

После иерархического воспроизведения проблемы устанавливаются приоритеты критериев и оцениваются каждая из альтернатив по критериям. В МАИ элементы задачи сравниваются попарно по отношению к их воздействию на общую для них характеристику. Система попарных сведений приводит к результату, который может быть представлен в виде обратно симметричной матрицы. Элементом матрицы  a_(i,j) является  интенсивность проявления элемента иерархии i относительно элемента иерархии j,  оцениваемая по шкале интенсивности от 1 до 9, предложенной автором метода, где оценки имеют следующий  смысл:

1 -  равная важность; 3 -  умеренное превосходство одного над другим; 5 -  существенное превосходство одного над другим; 7 - значительное превосходство одного над другим;  9 -  очень сильное превосходство одного над другим; 2, 4, 6, 8 - соответсвующие промежуточные значения.

Если при сравнении одного фактора  i  с другим j получено a(i,j)=b, то при сравнении второго фактора с первым получаем a(j,i)=1/b.

Опыт показал, что при проведении попарных сравнений в основном ставятся следующие вопросы. При сравнении элементов А и Б: какой из них важнее или имеет большее воздействие; какой из них более вероятен; какой их них предпочтительнее.

Относительная сила, величина или вероятность каждого отдельного объекта в иерархии определяется оценкой соответствующего ему элемента собственного вектора матрицы приоритетов, нормализованного к единице. Процедура определения собственных векторов матриц поддаётся приближению с помощью вычисления геометрической средней.

Весьма полезным побочным продуктом теории является так называемый индекс согласованности (ИС), который даёт информацию о степени нарушения согласованности. Вместе с матрицей парных сравнений мы имеем меру оценки степени отклонения от согласованности. Если такие отклонения превышают установленные пределы, то тому, кто проводит суждения, следует перепроверить их в матрице.

                       ИС=(lmax-n)/(n-1),

где n – число сравниваемых   элементов.   Для   обратносимметричной   матрицы   всегда lmax?n.
Теперь сравним эту величину с той, которая получилась бы при случайном выборе количественных суждений из шкалы 1/9, 1/8, 1/7,..., 1,2,....9, но образовании обратносимметричной матрицы. Ниже даны средние согласованности для случайных матриц разного порядка.

Таблица. Принцип синтеза. Произведя все расчёты, получим окончательную таблицу, в которой виден наиболее приемлимый вариант.

Вариант 1, в котором была не очень хорошо развита информационная обеспеченность тпредприятия, степень полноты и точности информации, необходимой для принятия эффективных инновационных решений стал наиболее приемлимым. При анализе можно убедиться, что исход не был удивительным, если принять во внимание то, что Вариант 1 превосходил остальные варианты. Однако, чтобы точно сделать выбор что лучше, необходимо произвести вычисления, чтобы не сделать неправильный выбор.