In the paper, we outline the main directions of investigation of the processes of interaction of bodies with regard for heat release. We describe analytic methods in more detail as compared with other approaches, because, to our mind, they are very promising for deriving simple engineering relations for braking processes on the basis of the equations of the thermal dynamics of friction.

Brakes are among the most widespread units with nonstationary friction. Braking friction systems are used for damping the kinetic energy of rotational or translational motion of masses by friction forces. By braking, one can decrease the velocity of relative sliding to zero (a stop) or to the given value (a snubbing). In the course of operation of braking units, all parameters of the process (velocity, load, temperature, physicomechanical and friction-wearing characteristics of materials of a couple, and conditions of contact) vary. To a great extent, their intensity is determined by the temperature of a friction contact. In particular, the temperature can be greater than admissible (critical) values for a given material, which leads to undesirable effects, such as local score and grasping. As a result, this can worsen conditions in the contact zone, namely, a decrease in the areas of contour and nominal regions as well as an increase in the temperature and its nonuniformity, which can violate the normal operation of a friction unit.

For the calculation of the thermal characteristics of brakes, one measures the contact temperature or determines it on the basis of a relevant mathematical model. It is a difficult problem to measure the maximum temperature of the zone of friction contact, because the time of existence and the size of actual contact regions where heat is generated are very small. In particular, it was established, that the contact region (pic. 1) is approximately circular with a mean diameter of 30 – 40 μm and, depending on its sizes, the time of existence of the region varies from 0.1 to 1 μsec.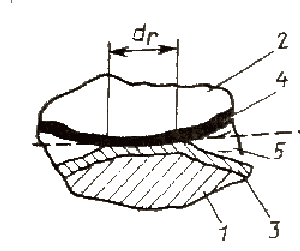

Picture 1 – Actual contact regions in diameter dr: 1, 2 – frictional elements; 3,4 – superficial slicks on elements; 5 – the intermediate environment.

However, the response time of even supersensitive thermocouples is greater than the time of existence of actual contact regions by more than one order of magnitude.

In the process of braking, the physicomechanical state of the surfaces of friction elements is determined not only by the contact temperature but by the nonstationary temperature field as well. In particular, for determination of the effective depth of warming-up (the near-surface layer where the mechanical and friction properties of materials vary), it is necessary to take into account temperature gradients. There are certain functional relations between these temperature gradients and the kinematic and dynamic parameters of the braking process, properties of a material, modes and methods of cooling, and other characteristics.

In some works for the operating characteristics of brakes (changes in the frictional moment, velocity, and duration of braking, etc.) give these relations and demonstrate the influence of temperature gradients on the thermal mode of the process of braking and physicomechanical properties of materials of a friction couple.

The computational model for estimation of the temperature in the zone of friction contact takes into account the discreteness of contact and the volumetric and surface heating of materials of the friction couple in the process of braking. The maximum temperature is presented in the form

where T₀ and T_V are the initial and bulk temperatures of an element of the couple before the n th cycle of operation,

T_C is the mean temperature of the surface of friction,

T^* is the flash temperature, which is superfluous over mean temperature of the surface of friction (arising at impact of microroughnesses).

Mean temperature is necessary for calculating for estimation of changes which can occur in a material layer. Maximum temperature of surface of a friction defines character course of physical and chemical processes on stains of actual contact, and also value of deterioration.