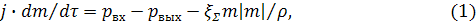
Источник: "Сборник научных трудов студентов физико-металлургического факультета ДонНТУ" - Донецьк, ДонНТУ - 2009.
В работе тепловых сетей мы часто сталкиваемся с процессами заполнения труб теплоносителем. При анализе этого процесса применяется, среди прочего, уравнение движения жидкости:
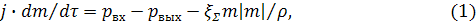
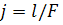- коэффициент инерционных потерь, где 
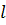- длина магистрали, м, 
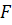- площадь проходного сечения участка магистрали, м^2; 
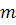- массовый расход жидкости, кг/с; 
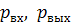- давление на входе и выходе из магистрали, Па; 
- плотность жидкости, кг/м^3; 
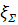- суммарный коэффициент гидравлических потерь, м^(-4). Подобные дифференциальные уравнения решаются путем численного интегрирования. Существуют две большие группы численных методов – многошаговые разностные методы и методы Рунге – Кутта, которые дают наиболее устойчивые решения, но с затратой большего количества времени. Основная идея методов Рунге – Кутта состоит в том, что производные аппроксимируются через значения функции 
в точках на интервале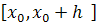 
, которые выбираются из условия наибольшей близости алгоритма к ряду Тейлора. Классический метод Рунге – Кутта состоит в том, что последующее значение функции вычисляется по формуле:
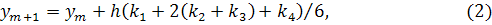
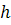- шаг; 
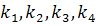- коэффициенты, вычисляемые по формулам: 
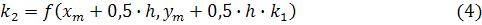
Определим закон изменения расхода воды в трубопроводе после мгновенного открытия задвижки перед баком (рисунок 1). Длина трубопровода равна L=10 м, диаметр d=0,03 м, высота столба жидкости в баке Н=12м. Давления на входе в бак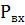 
и на выходе из трубопровода 
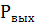будут равны атмосферному. Зададим начальные условия: 
; m=0 кг/с;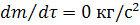 
, что соответствует моменту времени до открытия задвижки. Шаг по времени для интегрирования примем h=0,1 с. Коэффициент 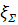будет складываться из коэффициента местных потерь на входе в трубу из бака 
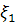и коэффициента путевых потерь давления в трубопроводе 
:
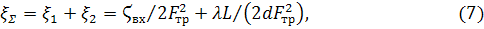
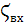– значение местного сопротивления на входе; 
– площадь проходного сечения трубы;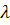 
– коэффициент потерь на трение.
Рисунок 1. Схема установки
По таблице сопротивлений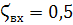 
. Для турбулентного режима течения коэффициент потерь на терние 
. Таким образом, 
.
При решении поставленной задачи дополнительно рассматриваем уравнение заполнения трубопровода:
где 
, V - текущий и общий объем заполняемого трубопровода, м^3.
Интегрируем уравнения (1) и (8) используя уравнения (2)-(6), программируя эти действия в Turbo Pascal. Полученные результаты представим в виде графиков (рисунок 2).
(а)
(б)
Рисунок 2. Изменение расхода воды (а) и скорость изменения расхода (б)
Анализируя результаты исследований, полученных с помощью классического метода Рунге – Кутта, видим, что установление расхода в трубопроводе при заданных условиях достигается за 1,4 секунды. Таким образом, можно сделать вывод, что полученные данные не противоречат физическому смыслу рассмотренного процесса.