Источник: http://www.cs.stevens.edu/~quynh/papers/rbf_modeling.pdf

В последние годы аналитически неявныем поверхностям, состоящим из радиальных базисных функций (RBFs), уделяется большое внимание. В этой статье мы представляем методы для расчета и визуализации неявных поверхностей, представленных суммированием взвешенных RBFs. Мы используем RBF с компактным носителем и дискретные образцы 3D базисных функций в 3D текстуре, которая отображается на перекрывающихся кубах сконцентрированных на точках поверхности. Мы используем графический процессор для вычисления значения неявной функции на всех отображаемых пикселях и непосредственно отображаем затененную изоповерхность без получения полигонального представления.

1. Введение

В работе предложен метод вычисления (или определения) и визуализации неявных поверхностей представленных как сумма взвешенных радиальных базисных функций (RBFs). Неявные поверхности могут описывать формы произвольной топологии и замкнутые поверхности, не требующие сшивания. Аналитические неявные функции, такие же, как используемая нами, более компактны, чем дискретные представления и могут быть определены в произвольном разрешении. Неявные поверхности остаются трудными для визуализации и интерактивной манипуляции, поскольку они требуют поиска корней, для нахождения поверхности. Стандартный метод для визуализации и взаимодействия с неявными поверхностями состоит в том, чтобы сначала получить явное представление (сетку), используя Марширующие кубы [7]. Получение изоповерхности крайне не интерактивно, хотя, и не является подходящим для моделирования приложений, в которых поверхность изменяется. Другие стандартные методы визуализации неявных поверхностей это трассировка лучей [6] и объёмная визуализация [2].

Эти алгоритмы визуализации высокого качества идеально подходят для создания неподвижных изображений, но обычно не достаточно подходят для интерактивной визуализации. Современные интерактивные алгоритмы трассировки лучей полагаются на предварительную сортировку сцены и не будут эффективными для изменения поверхностей. Неявные поверхности также были визуализированы с помощью динамических частичных систем [13]. В работе [4], Хартет расширяет эти идеи для рассмотрения более сложных неявных форм и представляет систему, которая может поддержать любое неявное представление поверхности. К сожалению, количество точек поверхности, используемых в качестве ограничений, ограничивается десятками, а не сотнями.

Вместо этого, мы разрабатываем менее «сеточный» подход, который использует графическое оборудование для выполнения интерполяции, взвешивания и суммирования RBFs. Мы берем за основу RBF с компактным носителем в качестве текстуры (2D для неявных контуров и 3D для неявных поверхностей), которые отображается на кубах (или квадраты для 2D-контуров) сконцентрированных на точках поверхности. Затем мы используем GPU для применения весов к RBF, хранимой в текстуре, аккумулируем RBF, формируя неявную функцию и визуализируем затененную изоповерхность без получения полигонального представления согласно подходу, основанного на работе Вестерманна [12]. Для повышения эффективности рендеринга, мы вычисляем только фрагменты, которые можно увидеть в видозависимом формате.

В Разделе 2 мы рассмотрим работу в неявных представлениях с помощью RBFs и GPU методов отображения неявных поверхностей. Мы предлагаем обзор нашего подхода в Разделе 3, описываем метод вычисления и отображения неявных поверхностей в разделе 4, а также обсуждаем результаты в разделе 5.

2. Связанные работы

2.1. Неявные функции, состоящие из RBFs

В последние годы аналитически неявныем поверхностям, состоящим из радиальных базисных функций (RBFs), уделяется большое внимание [1, 3, 8, 9].

2.2. Оптимизация отрисовки для неявных поверхностей

В работе [9], Рейтер и др. авторы используют сферу для ограничения пространства, порожденного RBF расположенного на поверхности. Они проецируют каждую сферу на плоскость изображения и для каждого пикселя результирующего диска они вычислят 3D точку поверхности путем интерполяции между ближней и дальней плоскостями касательных к сфере. Их производительность составляет порядка нескольких секунд на кадр для моделей из нескольких сот RBFs (например, 2.1 секунды для Стэндфордского Зайчика с 450 RBFs).

Более похожая работа содержится в [5], где Чан и др. используют усеченные гауссианы, для выполнения рассеянных интерполяций набора данных. Они пространственно разделяют RBF закодированный объем, в результате чего клетки содержат различное количество RBFs. Для каждого фрагмента, шейдер получает доступ к центрам RBF и весам, хранимым в текстурах, и вычисляет значения неявной функции по определению случайных гауссовских RBFs на фрагменте. Это требует больших затрат вычислений шейдера, что вызывает экспоненциальную функцию в цикле обхода всех RBFs в ячейке и переключение контекста между фрагментарными шейдерами, обрабатывающими циклы разных размеров. Мы также оцениваем значение неявной функции для каждого фрагмента. Однако, наш подход полностью отличается и содержит меньший объем вычислений для фрагментарных шейдеров.

3. Обзор

Нами разработаны приложения для визуализации и редактирования неявных поверхностей состоящих из RBFs. Наша система загружает точки ограничений, где сосредоточены RBFs, находит решение для весов, используя сопряженные градиенты, и непосредственно рассчитывает и отображает неявную поверхность на GPU. После того, как неявная поверхность была загружена, пользователь может работать с поверхностью, выбрав регион на поверхности, и перемещать ее (рис. 2b). В соответствии с тем как пользователь редактирует поверхность, обновляются веса через повторное решение матричной системы в программном обеспечении. Наша система определяет и отображает неявные поверхности на каждом кадре, так что поверхность визуализации одновременно обновляется по мере обновления весов. В следующем разделе мы описываем новые компоненты нашей системы, а именно вычисление и отображение неявной поверхности.

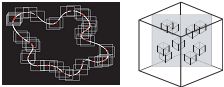
(a)           (b)

Рисунок 1: (a) Квадраты в 2D RBFs отображены в текстуре и выделены в верхнем изоконтуре.
(b) Срез 3D области пересекает множественные RBFs.

4. Вычисление и рендеринг точечных неявных поверхностей

При разработке нашей неявной системы моделирования, мы адаптируем идеи из работы Вестерманна и др. [12] для интерактивного объемного рендеринга и из работы Стрзодка [10] для вычисления протяженности полей. В работе [10], Стрзодка вычисляет преобразование 2D расстояния с помощью предварительного вычисления произвольно установленных 2D функций расстояния от точки и храня протяженность поля в текстуре. Протяженность поля для заданной формы затем генерируется ренденингом предварительно вычисленной текстуры с центром в каждой точке границы с режимом смешивания установленным в GL_MIN. В нашем подходе, мы сохраняем дискретные версии финитных RBF в текстуре. Для 2D контуров, мы отрисовываем квадрат с центром в точках на контуре и текстуру площади с 2D RBF функцией. Вместо смешивания, фрагмент Shader применяет вес связанный с каждым RBF и аккумулирует взвешенные значения RBF на каждый пиксель, как каждая клетка, отрисовавается, как показано на рисунке 1a.

Неявная функция значения каждого пикселя, накапливается в pbuffer. Обратите внимание, что pbuffers может хранить знаковые значения с плавающей точкой. Текстурирующая аппаратура выполняет интерполяцию текстурных координат и текстурных значений, с тем, что каждый пиксельный образец функции RBF в точке с координатами соответствует пиксельному расстоянию от центра RBF. В конце концов RBFs были обрисованы в pbuffer, и изоконтур тогда отображазится при прохождении только через фрагменты, которые имеют общее нулевое значение. Мы снова используем шейдерный фрагмент, чтобы проверить и передать, или отклонить фрагменты. Обратите внимание: чтобы добавить полиномиальные компоненты, мы отрисовываем четырехсторонник охватывающий весь домен, текстурированный с линейными весами.

К сожалению, вычисление и прорисовка 3D неявных поверхностей не простая задача, так как графическое оборудование прорисовывает только 2D буферы, а не 3D объемные изображения. Uberbuffers ATI предоставляют возможность отображения непосредственно в 3D текстуры, но только один фрагмент 2D может быть отображен в 3D текстуру в момент времени. Таким образом, выборка 3D RBF, которая находится в 3D текстуре, не может быть вычислена и отображена непосредственно в объеме за один проход, как это было сделано для 2D неявной функции. Основываясь на подходе, описанном в [12], для интерактивного объемного отображения для 3D неявной функции посредством отображения 2D разреза 3D RBF текстуры. В работе [12], Вестерманн отрисовывает плоскости, параллельные плоскости изображения, которые обрезаны напротив 3D текстур домена. Аппаратные интерполяции 3D-координат текстуры и смешивает последовательные параллельные плоскости, которые были текстурированы, с объемом данных. Вместо одной 3D текстуры, которая охватывает полный объем, мы имеем RBF текстуру, которая отображается на разных местах и в каждом месте, охватывая лишь небольшой куб с размерами равными радиусу RBF.

Как и в [12], мы вычисляем плоскости, параллельные плоскости изображения, которое мы называем разрезающей плоскостью. Каждая разрезающая плоскость пересекается с кубом, ограниченным RBFs, как показано на рисунке 1b. Для каждого куба, который проектируется на плоскость нарезки, результатом пересечения является четырехугольник или треугольник, который является текстурированным с использованием 3D текстурных координат, полученных от пересечения. Как и при вычислении 2D неявной функции, текстурированный четырехугольник или треугольник отображается с учетом соответствующего RBF и накапливаются в pbuffer для каждой разрезающей плоскости.

Литература

[1] Carr, J., R.K. Beatson, J.B. Cherrie, T.J.Mitchell,W.R. Fright, and B.C. McCallum. “Reconstruction and Representation of 3D Objects With Radial Basis Functions”, Computer Graphics Proceedings (SIGGRAPH 2001), August 2001, pp.67–76.

[2] Drebin, R.A., L. Carpenter, P. Hanrahan. “Volume Rendering”, Computer Graphics Proceedings (SIGGRAPH 88), pp.65–74.

[3] Dinh, H.Q., G. Turk, and G. Slabaugh. “Reconstructing Surfaces By Volumetric Regularization Using Radial Basis Functions”, IEEE PAMI, October 2002, pp.1358–1371.

[4] Hart, J.C., E. Bachta, W. Jarosz., and T. Fleury. “Using Particles to Sample and ControlMore Complex Implicit Surfaces” Proceedings of Shape Modeling International 2002, May 2002.

[5] Jang, Y., M. Weiler, M. Hopf, J. Huang, D.S. Ebert, .P. Gaither, and T. Ertl. “Interactively Visualizing Procedurally Encoded Scalar Fields”, Proceedings of Eurographics Symposium on Visualization, 2004.

[6] Levoy, M. “Ef?cient Ray-Tracing of Volume Data”, ACM Transactions on Graphics, July 1990, Vol.9(3), pp.245–261.

[7] Lorensen, W. and H.E. Cline, “Marching Cubes: A High Resolution 3-D Surface Construction Algorithm,” Computer Graphics (SIGGRAPH 87), Vol.21(4), July 1987, pp. 163–169.

[8] Morse, B.S., T.S. Yoo, P. Rheingans, D.T. Chen, and K.R. Subramanian. “Interpolating Implicit Surfaces from Scattered Data Using Compactly Supported Radial Basis Functions” Proceedings of Shape Modeling International, May, 2001, pp.89–98.

[9] Reuter, P., I. Tobor, C. Schlick, and S. Dedieu. “Pointbased Modelling and Rendering Using Radial Basis Functions”, Proceedings of 1st Intl Conf. on Computer Graphics and Interactive Techniques in Australasia and South East Asia, Feb. 2003, pp.111–118.

[10] Strzodka, T. “Generalized Distance Transforms and Skeletons in Graphics Hardware”, Proceedings of Symposium on Visualization, 2004.

[11] Wendland, H. “Piecewise Polynomial, Positive Definite and Compactly Supported Radial Functions of Minimal Degree”, Advances in Computational Mathematics, 1995, Vol.4, pp.389–396.

[12] Westermann, R. and T. Ertl. “Ef?ciently Using Graphics Hardware in Volume Rendering Applications”, Computer Graphics Proceedings (SIGGRAPH 98) July 1998, pp.169–177.

[13] Witkin, A. and P. Heckbert. “Using Particles to Sample and Control Implicit Surfaces”, Computer Graphics Proceedings (SIGGRAPH 94), pp.269–277.