|
До настоящего времени продолжается совершенствование моделей данного вида. Так, созданы различные версии модели TUPOS [2], в которых учитывается влияние направления и величины скорости ветра на уровень струи, более детально моделируется взаимодействие с лежащим выше струи теплым слоем воздуха, уточняются коэффициенты в модели.
В некоторых случаях лучшего соответствия экспериментальным данным достигают за счет некоторого упрощения модели. Так, в качестве вертикальной дисперсии струи используют высоту слоя перемешивания, что для условий развитой атмосферной конвекции дает хорошие результаты.
Модель Института экспериментальной метеорологии (ИЭМ). По видимому, наиболее совершенная из практически применяемых отечественных моделей. Практическая форма модели изложена в [3] как официальная модель для расстояний до 100 км. Научные основы модели и ее сравнение с моделью Паскуилла-Гиффорда (и с некоторыми другими) приведены в [4].
Эта модель в равной степени пригодна для описания распространения облака, созданного мгновенным источником, и струи от непрерывного источника. Распределение концентрации примеси по всем трем координатам имеют гауссову форму, как и в модели Паскуилла-Гиффорда, однако положение центра облака или струи находят интегрированием кинематического уравнения: 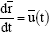 , где: u(t) — скорость ветра в точке, где облако находится в настоящий момент; r — вектор координат центра облака; t — время движения. , где: u(t) — скорость ветра в точке, где облако находится в настоящий момент; r — вектор координат центра облака; t — время движения. Основные работы: «Доказательства и опровержения» (1964), «Фальсификация и методология научно-исследовательских программ» (1970), «История науки и ее рациональные реконструкции» (1972), «Изменяющаяся логика научного открытия» (1973) и др.
Процесс диффузии в перпендикулярных к ветру направлениях рассматривают как функцию времени, в отличии от чисто пространственных распределений в модели Паскуилла – Гиффорда. Таким образом, модель включает важные свойства так называемых моделей “лагранжева облака”. Это обеспечивает возможность учета изменения направления и скорости ветра в процессе распространения облака, что позволяет применять модель для расстояний, много больших 10 км.
Зависимость дисперсий облака по всем координатам как функции от времени задают формулами, в которые входит параметр Монина – Обухова, заменяющий в качестве характеристики устойчивости атмосферы классы устойчивости Паскуилла. В модели учитывается поворот и изменение модуля скорости ветра с высотой.
Данная модель при наличии только простейших метеоданных, то есть однократного измерения скорости и направления на уровне флюгера, почти не имеет преимуществ по сравнению с моделью Паскуилла – Гиффорда. Ее преимущества реализуются с увеличением входной информации.
В модели используется карта свойств подстилающей поверхности, которая должна быть создана с учетом сезонной зависимости.
Одним из направлений развития таких моделей является подключение к ним модели пространственного распределения скорости ветра, простейший учет сложного рельефа в которой реализован при расчете течений воздуха в предположении его потенциальности. Хотя это предположение плохо соответствует наличию турбулентной вязкости, из-за математической простоты оно применяется достаточно широко. Таким путем, как сообщалось в [5], совершенствуется официальная модель США, которая создана и поддерживается Агенством по охране окружающей среды EPA.
Трехмерные модели переноса и диффузии примеси и их упрощенные варианты. В обзоре МАГАТЭ [6] рассмотрены три типа моделей: Гаусовские, модели Лагранжева облака и трехмерные модели. Основное отличие трехмерных моделей состоит в явном расчете диффузии и переноса примеси. Компоненты скорости ветра, коэффициенты тензора диффузии и плотность источника примеси при решении уравнения рассматривают как заданные функции. Для задания коэффициентов тензора диффузии используются различные эмпирические модели атмосферной турбулентности, в которых необходимо прежде всего задать распределение скорости ветра. К определению пространственного распределения скорости ветра есть принципиально различные подходы.
Авторы обзора МАГАТЭ выражают скептическую точку зрения: не существует моделей, которые позволили бы предсказывать поле ветров на масштабах 10-100 км. Поэтому они считают единственным путем методы экстраполяции и интерполяции данных непосредственных измерений. При этом строится распределение ветра по высоте на многих уровнях на достаточно подробной горизонтальной сетке. Такой путь может быть обобщен за счет типизаций метеоусловий, что позволяет привлечь измерения, выполненные ранее. В любом случае, это большая метеорологическая работа, требующая организации сети постоянно действующих метеодатчиков.
Существует более оптимистичная точка зрения. О моделировании течений воздуха на масштабах десятков километров вокруг Новосибирска сообщалось в обзорном докладе на II Всероссийской конференции по математическим проблемам экологии. В такой модели входными являются уже иные параметры: ветер в свободной атмосфере, температура почвы и воды, тепловыделение предприятий, рельеф, шероховатость, и т.д.
Существует класс двумерных моделей. Для города такое допущение соответствует предположению о неизменности всех параметров.
Трехмерные модели имеют важные преимущества. Учитываются высотные распределения ветра и температуры, взаимодействие примеси с подстилающей поверхностью может быть учтено в качестве граничного условия в настолько полной форме, насколько известна природа этого процесса. Могут быть учтены различные вариации параметров атмосферы и поверхности в течении суток и от сезона к сезону.
Но отсутствие необходимых данных для использования 3-х мерных моделей и инфраструктуры для их использования (реальных заказов и квалифицированных пользователей) не позволяют рассчитывать на их практическое применение в ближайшем будущем, и эти модели остаются научно-исследовательскими.
Существует ряд упрощенных моделей. Так, в [7], при дополнительном предположении о постоянстве коэффициентов в уравнении переноса-диффузии при некоторых более сложных предположениях построены аналитические решения. Однако этот путь в нашей стране также считается нецелесообразным, так как решения достаточно сложны, а реальные распределения коэффициентов слишком огрубляются.
Наиболее перспективной является реализация упрощенного варианта, в котором оставлена одна диффузия по высоте, как это предложено в модели [8].
Перспективы развития моделей в соответствии с рекомендациями МАГАТЭ. При анализе различных моделей распространения примесей в атмосфере, пригодных для оценки аварий на объектах, атомной энергетики, в обзоре МАГАТЭ [6] представлены 3 типа моделей: гауссовы модели, модели лагранжева облака и трехмерные модели. Гауссовы модели являются в настоящее время рабочими моделями в МАГАЭ, последние 2 типа моделей названы как перспективными, и уже используются в некоторых странах для повышения обоснованности экспертных заключений.
Выводы. Модели, используемые в научных исследованиях, в основном создаются как инструмент исследования природы и носят причинно-следственный характер. В их использовании сложились определенные технологии, понятийный и математический аппарат, условия и традиции. Иногда даже говорят о культуре физико-математического моделирования.
В задачах экологической экспертизы, оценки и даже прогноза качества окружающей среды чаще всего используются описательные или имитационные модели. В них, прежде всего, стремятся получить ответы на вопросы “Какое загрязнение окружающей среды произойдет при тех, или иных условиях?”. В таких случаях необходимо получить ответ, адекватный ситуации, а не устанавливать причинно-следственные связи.
В целом выбор математической модели в значительной степени зависит от реализуемых задач.
Литература
1. Методика прогнозирования масштабов заражения сильнодействующими ядовитыми веществами при авариях (разрушениях) на химически опасных объектах и транспорте. Руководящий документ РД 52.04.253-90. Л.: Гидрометеоиздат.
|














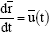 , где: u(t) — скорость ветра в точке, где облако находится в настоящий момент; r — вектор координат центра облака; t — время движения.
, где: u(t) — скорость ветра в точке, где облако находится в настоящий момент; r — вектор координат центра облака; t — время движения.