 |
В данной работе рассматривается математическая модель прогнозирования распространения загрязнения в атмосфере по данным автоматизированного поста наблюдения, который расположен на территории ДонНТУ и функционирует с ноября 2008 года. Данный пост контролирует концентрации оксида углерода (CO), диоксида серы (SO2) и диоксида азота (NO2) в воздухе. Процесс измерения включает анализ атмосферного воздуха с помощью газоанализатора, в состав которого входят датчики CO, SO2 и NO2, далее с периодичностью 10 минут значения концентраций веществ записываются в базу данных. Накопленная информация о концентрациях представляет собой временной ряд, включающий больше 20 тысяч наблюдений, для анализа и прогнозирования которых требуются большие вычислительные мощности. В данных временных рядах возможны ошибки – пропуски, связанные с наладкой работы поста, и погрешности датчиков. Для снижения степени влияния этих ошибок в работе применялась интерполяция по соседним точкам (для заполнения пропусков) и сглаживание методом скользящего среднего (для удаления шума).
Данные временные ряды позволяют строить модели прогноза загрязнения атмосферы. При этом могут быть использованы следующие методы: анализ прерванных временных рядов; экспоненциальное сглаживание и прогнозирование; спектральный анализ (Фурье); авторегрессии и проинтегрированного среднего (ARIMA-АРПСС); прогнозирование с использованием нейронных сетей и другие [2]. В данной работе использовались последние два метода.
Метод авторегрессии и проинтегрированного скользящего среднего (АРПСС) основан на использовании процессов авторегрессии и скользящего среднего. Имеется три типа параметров модели: параметры авторегрессии (p), порядок разности (d), параметры скользящего среднего (q). В обозначениях Бокса и Дженкинса модель записывается как АРПСС (p, d, q). После идентификации модели производится оценивание параметров модели. Полученные оценки параметров используются при выполнении прогноза [2].
Для решения задач прогнозирования также может использоваться нейросетевой подход. Он состоит в построении оптимальной нейронной сети на основе исходных данных, её обучении по различным алгоритмам (алгоритм обратного распространения, метод спуска по сопряженным градиентам и др.), построении прогноза. Преимущество данного метода – то, что прогноз можно выполнять на любое число шагов [1].
Результаты построения моделей методом АРПСС в среде STATISTICA 6.0 для временного ряда концентраций CO в атмосфере приведены в таблице 1.
Таблица 1 – Идентификация модели динамики временного ряда CO
| № | p1 | p2 | d | q1 | q2 | MS residuals | Mx | Dx |
| 1 | 0,99977 | - | 0 | - | - | 0,00070 | 0,00014 | 0,00074 |
| 2 | 0,99998 | - | 0 | 0,46467 | - | 0,00180 | 0,00013 | 0,00161 |
| 3 | 1,6598 | -0,6603 | 0 | - | - | 0,00039 | 0,00018 | 0,00062 |
| 4 | - | - | 0 | -0,9910 | - | 0,28921 | 0,16567 | 0,04323 |
| 5 | - | - | 0 | -1,845 | -0,9462 | 0,08358 | 0,08701 | 0,01940 |
| 6 | - | - | 1 | -0,6451 | 0,35491 | 0,00030 | -0,00010 | 0,00022 |
| 7 | 0,89782 | - | 1 | - | - | 0,00010 | -0,00001 | 0,00008 |
| 8 | 0,74186 | - | 1 | -0,9970 | 1 | 0,00007 | -0,00001 | 0,00005 |
| 9 | 1,1596 | -0,2915 | 1 | - | - | 0,00009 | -0,00001 | 0,00007 |
| 10 | 0,58667 | 0,20897 | 1 | -0,9976 | - | 0,00006 | -0,00001 | 0,00006 |
| 11 | 1,0221 | -0,1118 | 1 | -0,5316 | 0,46465 | 0,00006 | -0,00001 | 0,00005 |
Исходя из минимума среднего квадрата остатков видно, что наилучшей моделью является модель АРПСС(2,1,2), уравнение которой имеет вид:
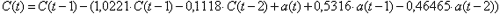 (1) (1)
где: C(t) – концентрация CO в текущий момент времени, C(t-i) – концентрация в предыдущие моменты времени, a(t) – значение белого шума в текущий момент времени (его параметры Mx=-0,00001, Dx=0,00005), a(t-i) – значение белого шума в предыдущие моменты времени.
|
 |














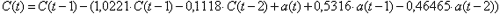 (1)
(1)