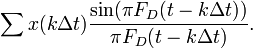Теорема Котельникова

Материал из Википедии — свободной энциклопедии

Теоре?ма Коте?льникова (в англоязычной литературе — теорема Найквиста-Шеннона) гласит, что, если аналоговый сигнал x(t) имеет ограниченный спектр, то он может быть восстановлен однозначно и без потерь по своим дискретным отсчётам, взятым с частотой более удвоенной максимальной частоты спектра F_max:

f_дискр > ${2 \cdot F_{max}},$

где F_max — верхняя частота в спектре, или (формулируя по-другому) по отсчётам, взятым с периодом чаще полупериода максимальной частоты спектра F_max:

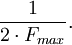
T_дискр < $\frac{1}{2 \cdot F_{max}}.$

[править] Пояснение

Такая трактовка рассматривает идеальный случай, когда сигнал начался бесконечно давно и никогда не закончится, а также не имеет во временной характеристике точек разрыва. Именно это подразумевает понятие «спектр, ограниченный частотой F_max».

Разумеется, реальные сигналы (например, звук на цифровом носителе) не обладают такими свойствами, так как они конечны по времени и, обычно, имеют во временной характеристике разрывы. Соответственно, их спектр бесконечен. В таком случае полное восстановление сигнала невозможно и из теоремы Котельникова вытекает 2 следствия:

Любой аналоговый сигнал может быть восстановлен с какой угодно точностью по своим дискретным отсчётам, взятым с частотой

f_дискр > ${2 \cdot F_{max}},$

где F_max — максимальная частота, которой мы ограничили спектр реального сигнала.

Если максимальная частота в сигнале превышает половину частоты прерывания, то способа восстановить сигнал из дискретного в аналоговый без искажений не существует.

Говоря шире, теорема Котельникова утверждает, что непрерывный сигнал можно представить в виде следующего ряда:

$\sum x(k\Delta t) \frac{\sin ( \pi F_{D}(t - k\Delta t))}{\pi F_{D}(t - k\Delta t)}.$

Под интегральной суммой написана формула отсчётов функции x(t). Мгновенные значения этой функции есть значения дискретизированного сигнала в каждый из моментов времени.