Вклады CWI в усовершенствование параллельных методов Рунге-Кутты

Авторы: Хоувен П.Д., Соммейер Б.П.
Переводчик: Душинская Н.А.
http://ftp.cwi.nl/CWIreports/NW/NM-R9608.pdf

Резюме

Эта работа рассматривает вклады CWI, которые направлены на усовершенствование параллельных методов Рунге-Кутты (РК). Мы опишем два подхода для построения таких методов. В обоих подходах обычный неявный метод Рунге-Кутты используется в качестве корректора уравнения, решение которого апроксимируется итерационным методом. В первом подходе итеративный метод использует фиксированное количество итераций без решения корректора. Предположим, что используется одношаговый предиктор, этот подход снова приводит к методу РК, однако, метод РК обладает большим внутренним параллелизмом. Во втором подходе, корректор решен модифицированной итерацией Ньютона и линейные системы, возникающие в каждой итерации Ньютона, решаются параллельным итерационным процессом, который настроен на специальный формат этих линейных систем. Кроме того, мы используем параллельный итерационный процесс на шаге параллельной обработки, который дополнительно повышает уровень параллелизма. Наконец, кратко обсудили применение параллельных методов РК в рамках уменьшения сигнала.

Ключевые слова и фразы: численный анализ, дифференциальные уравнения, методы Рунге-Кутты, параллелизм.

1. Введение

Мы будем иметь дело с решением начально-краевой задачей (НКЗ)

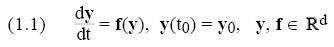
по методам Рунге-Кутты (РК) на параллельных компьютерах. Нашей стартовой точкой является метод РК.

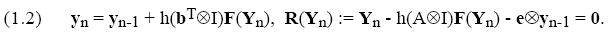
Где А – матрица Бутчера размерностью s на s;

B – S-мерный вектор, содержащий веса на шаге итерации;

Е – S-мерный вектор с единичными значениями;

I – единичная матрица размерностью d на d

h – размер шага t_n - t_n-i

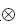- означает умножение Кронекера

S компоненты Y_ni из sd-мерного вектора решения Y_n представляют s численные аппроксимации s точечного решения вектора Y(et_n-i + ch) , где с = Ae обозначается абсциссой вектора. Кроме этого, для любого вектора V = (V_i), F(V) хранятся производные величины (f(V_i)). Предполагается, что компоненты с различны и расположены в порядке возрастания. В дальнейшем, мы будем использовать обозначение I для любой единичной матрицы. Однако, это всегда будет ясно из контекста.

Эта работа рассматривает вклады CWI, которые направлены на усовершенствование параллельных методов Рунге-Кутты (РК). Мы опишем два подхода для построения таких методов. В обоих подходах (1.2) используется в качестве корректора уравнения, решение которого апроксимируется итерационным методом. В первом подходе итеративный метод использует фиксированное количество итераций и (1.2) не обязательно будет решением. Предположим, что используется одношаговый предиктор, этот подход снова приводит к методу РК, однако, метод РК обладает большим внутренним параллелизмом. Во втором подходе, (1.2) решено модифицированной итерацией Ньютона и линейные системы, возникающие в каждой итерации Ньютона, решаются параллельным итерационным процессом, который настроен на специальный формат этих линейных систем. Разделы 2 и 3 описывают структуру и анализ параллельных методов РК и параллельных итерационных методов РК. В Разделе 4 параллельный итерационный процесс применяется на шаге параллельной обработки, который дополнительно повышает уровень параллелизма. Наконец, в 5 разделе кратко описывается применение параллельных методов РК в рамках уменьшения сигнала

2. Параллельные методы Рунге-Кутты

Рассмотрим метод

где B и C надлежащим образом выбранные матрицы и m фиксированное целое. Этот метод можно интерпретировать как итерационный метод с фиксированным числом итераций. Очевидно, что если 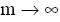и Y_n^(j) совпадают, то Y_n^(j) сводится к решению Y_n из (1.2). Однако, для фиксированной m, мы можем также интерпретировать ((2,1), (2.2), (2.3a)) по методу РК с таблицей Бутчера, которые приведены на рисунке 2.1a.

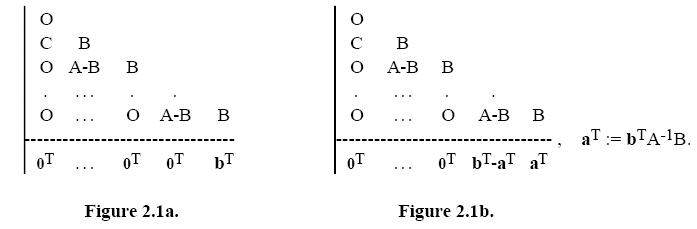
В случае жестких задач его рекомендуется заменить (2.3a) по формуле (см. Хайер и Ваннер [19, с.129], а Шaмпайн[46])

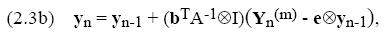
при условии, что А – невырожденная матрица (мы отметим, что для более точных методов РК, где b^T = e_s^TA, формула (2.3b) сводится к 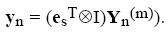Шаг в формулах (2.3a) и (2.3b) будет приведен в качестве обычного и шага в формуле Шaмпайна. Таблица Бутчера для {(2.1),(2.2).(2.3b)} приведена на рисунке 2.1b.

Методы типа (2,2) также могут быть основаны на более общих корректорах, чем формулы РК (для исследований мы ссылаемся на Буррагe [10, 11, 12] и [47]).

В целях обеспечения точности линейной устойчивости и степени параллелизма в методах ((2,1), (2.2), (2.3)) определяются детерминированные матрицы A, B и C. Мы имеем следующий результат порядка точности (см., например, Jackson и Nоrsett [34], Burrage [8, 9], van Dorsselaer [17], и CWI работах [22, 27]).

Теорема 2.1.

Порядок точности метода РК ((2,1), (2.2), (2.3a)) и ((2,1), (2.2), (2.3b)) соответственно представлен как p := min{p*,m+q+l} и p := min{p*,m+q}, где p* и q обозначим порядком точности корректора (1,2), а также формулы для предиктора Yn⁽⁰⁾. Если (B+C)e = c, то q > 1, и если также Bс = Ac, то q > 2.

Результаты для жесткого порядка точности приведены в [25]. Отныне, порядок метода всегда будет подразумевать не жесткий порядок точности.

Линейная устойчивость свойств достигается путем применения ((2,1), (2.2), (2.3)) к основному устойчивому тестовому уравнению 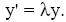Для определения шага формулы (2.3a) и (2.3b), это приводит к стабильности соответствующих функций

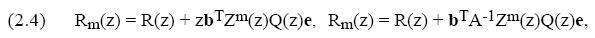
где z := hA, матрицы Z, Q и функция R получены из

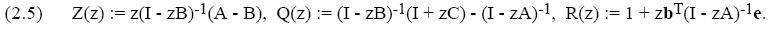
где, R(z) устойчивая функция корректора (1.2). В следующих разделах мы рассмотрим случаи, когда B является диагональной матрицей.

2.1. Явные методы РК

Для нежестких задач, мы можем задать B = C = O для получения четкого s(m+1)-значения метода РК требующего sm+1 оценок правой части. Поскольку в жестких ситуациях, вполне естественно, использование обычного шага по формуле (2.3a), теорема 2.1 подразумевает, что порядок точности задается p := min{p*,m+q+l} = min{p*,m+l}. Каждый блок на этапе s для метода PIRK можно распараллелить, так, что для m < p*-l, мы фактически имеем (m+1) этапов порядка m+1 (при условии, что задействовано s процессоров). Таким образом, для m < p*-l, {(2.1),(2.2),(2.3a)} выводится явный метод РК (метод ЯРК) порядок которого равен его числу эффективных(или продолжительных) этапов. Iserles и Nоrsett [33] показали, что это оптимальный результат, потому что порядок р явных методов РК, не может превышать числа s_seq последовательных этапов (см. также Nоrsett и Simonsen [44]). Если мы выбираем для основного корректора метод Гаусса-Лежандра s порядка, то P * = 2s, число процессоров задействованы наполовину. Устойчивость многочленов оптимальных методов ЯРК приведена в усеченных рядах разложения Тейлора exp(z), устойчивость в регионах можно найти в литературе (см., например, [19]).

Эксперименты на четырехядерном процессоре компьютера фирмы Alliant были проведены в университете Трондхейма [38] и на CWI[22]. Эти эксперименты показали, что вышеперечисленные параллельные методы РК довольно эффективны.

Замечание 2.1.

Оптимальные методы ЯРК также могут быть получены путем экстраполяции Ричардсона [23]. В частности, экстраполяция явной медианной нормы создает оптимальные методы ЯРК порядка p, которые используют только [1 + p / 4] процессоров (в данном случае, [.] обозначает целую часть функции). Тем не менее, в реальных вычислениях, они оказываются более дорогостоящими, чем методы Гаусса-Лежандра.

2.2. Диагональные неявные методы Рунге-Кутты

Параллельные диагональные неявные итерационные методы РК могут возникнуть, если B является диагонали матрицы D. Из-за неявности «диагонали», каждый блок на этапе s можно распараллелить, так, что фактически, мы будем имеем только m+1 неявных этапов. Устойчивость регионов можно выразить из устойчивых функций (2.4). В работе [27] и [24], это было сделано для нескольких вариантов: D = B и C. В таблице 2.1 определены основные характеристики некоторых из этих параллельных методов ДНРК. В целях сравнения мы также указали перечень характеристик обычных ДНРK методов и параллельных РК методов (ПРК)[33]. В этой таблице, p_st обозначает порядок этапа блока, s_seq количество неявных последовательных этапов, и K - необходимое количество процессоров. Кроме того, А - устойчивая, 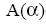-устойчивая, L-устойчивая и сильно А –устойчивая и 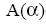-устойчивая, соответственно, указанные в A, 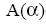, L>A and L> 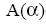. Из всех эти методов нужно только одно LU-разложение на процессор. Методы, указанные в пятой и шестой строке этой таблицы используют или Гаусса-Лежандра или Radau ИВР в качестве основополагающего корректора, как шаг точки в формуле (2.3a). В методах последние три строки, с корректором является Radau с шагом точки формуле (2.3b), и в методах двух последних строк, D определяется устойчивостью функции Wolfbrandt[50].

Порядок	pst	sseq	K	устойчивость	Примечания
p = 3	1	p-1	1	A	ДНРК, Norsett [42]
p=3	2	p-1	1	>A	ДНРК, Crouzeix [16]
p=4	1	p-1	1	A	ДНРК, Crouzeix [16], Alexander [1]
p=4	1	p-2	2	L	ПРК, Iserles & N0rsett [33]
p=3,4,5	s	p-1	s	>A	Параллельные ДНРК, C = O, D = diag(c), [27]
p=6,7	s	p-1	s		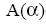Параллельные ДНРК, C = O, D = diag(c), [27]
p=3,5,7	s	p	s	>A	Параллельные ДНРК, C = A-D, p(I-D-1A)=0, [24]
p<=6,p=8	s	p	s	L	Параллельные ДНРК, C = O, D = 81, [27], [50]
p<=8,p=10	s	p+1	s	L	Параллельные ДНРК, C = O, D = 81, [27], [50]

Для метода ПРК Iserles и Nоrsett потребовалось удивительно малое количество последовательных этапов и в то же время это L-устойчивая. Параллельные методы ДНРК имеют преимущество - сравнительно высокий порядок и шаг порядка.

[1] Alexander, R. [1977]: Diagonally implicit Runge-Kutta methods for stiff ODEs, SIAM J. Numer. Anal. 14, 1006-1021.

[2] Augustyn, R. & Uberhuber, C.W. [1992]: Parallel defect correction algorithms for ordinary differential equations, ACPC/TR 92-22, Austrian Centre for Parallel Computation, Vienna, Austria.

[3] Bellen, A. [1987]: Parallelism across the steps for difference and differential equations, in: Numerical methods for ordinary differential equations, A. Bellen, C.W. Gear & E. Russo (eds.), Proceedings L'Aquila 1987, Lecture Notes in Mathematics 1386, Springer-Verlag, Berlin, 22-35.

[4] Bellen, A., Jackiewicz, Z. & Zennaro, M. [1993]: Time-point relaxation Runge-Kutta methods for ordinary differential equations, J. Comput. Appl. Math. 45, 121-137.

[5] Bellen, A., Jackiewicz, Z. & Zennaro, M. [1994]: Contractivity of waveform relaxation Runge-Kutta iterations and related limit methods for dissipative systems in the maximum norm, SIAM J. Numer. Anal. 41, 499-523.

[6] Bellen, A., Vermiglio, R. & M. Zennaro [1990]: Parallel ODE-solvers with stepsize control, J. Comput. Appl. Math. 31, 277-293.

[7] Burrage, K. [1978]: A special family of Runge-Kutta methods for solving stiff differential equations, BIT 18, 22-41.

[8] Burrage, K. [1991]: The error behaviour of a general class of predictor-corrector methods, Appl. Numer. Math. 8, 201-216.

[9] Burrage, K. [1993]: Efficient block predictor-corrector methods with a small number of corrections, J. Comput. Appl. Math. 45, 139-150.

[10] Burrage, K. [1993]: Parallel methods for initial value problems, Appl. Numer. Math. 11, 5-25, 1993.

[11] Burrage, K. [1993]: The search for the Holy Grail, or: Predictor-corrector methods for solving ODEIVPs, Appl. Numer. Math. 11, 125-141.

[12] Burrage, K. [1995]: Parallel and sequential methods for ordinary differential equations, Clarendon Press, Oxford.

[13] Butcher, J.C. [1976]: On the implementation of implicit Runge-Kutta methods, BIT 16, 237- 240.

[14] Butcher, J.C. [1979]: A transformed implicit Runge-Kutta method, J. Assoc. Comput. Mach. 26, 731-738.

[15] Chartier, P. [1993]: Parallelism in the numerical solution of initial value problems for ODEs and DAEs, Thesis, Universite de Rennes I, France.

[16] Crouzeix, M. [1975]: Sur l'approximation des equations differentielles operationnelles lineaires par des methodes de Runge-Kutta, Ph. D. Thesis, Universite de Paris.

[17] Dorsselaer, J.L.M. van [1994]: Theoretical aspects of numerical methods for initial value problems, PhD thesis, University of Leiden, The Netherlands.

[18] Gear, C.W. & Xu Xuhai [1993]: Parallelism across time in ODEs, Appl. Numer. Math. 11, 45- 68.

[19] Hairer, E. & Wanner, G. [1991]: Solving ordinary differential equations, II. Stiff and differential-algebraic problems, Springer-Verlag, Berlin.

[20] Hoffmann, W. & Swart, J.J.B. de [1995]: Approximating Runge-Kutta matrices by triangular matrices, Preprint NM-R9517, CWI, Amsterdam.

[21] Hout, KJ. in 't [1995]: On the convergence of waveform relaxation methods for stiff nonlinear ordinary differential equations, Appl. Numer. Math. 18, 175-190.

[22] Houwen, PJ. van der & Sommeijer, B.P. [1990]: Parallel iteration of high-order Runge-Kutta methods with stepsize control, J. Comput. Appl. Math. 29, 111-127.

[23] Houwen, PJ. van der & Sommeijer, B.P. [1990]: Parallel ODE solvers, in: Proceedings of the International Conference on Supercomputing, 1990, ACM Press, 71-81.

[24] Houwen, PJ. van der & Sommeijer, B.P. [1991]: Iterated Runge-Kutta methods on parallel computers, SIAM J. Sci. Stat. Comput. 12, 1000-1028.

[25] Houwen, PJ. van der & Sommeijer, B.P [1993]: Analysis of parallel diagonally implicit iteration of Runge-Kutta methods, Appl. Numer. Math. 11, 169-188.

[26] Houwen, PJ. van der & Sommeijer, B.P. [1995]: Iteration of Runge-Kutta methods with block triangular Jacobians, Preprint NM-R9506, CWI, Amsterdam (to appear in ZAMM 76).

[27] Houwen, PJ. van der, Sommeijer, B.P. & Couzy, W. [1992]: Embedded diagonally implicit Runge-Kutta algorithms on parallel computers, Math. Comp. 58, 135-159.

[28] Houwen, PJ. van der, Sommeijer, B.P. & Veen, W.A. van der [1995]: Parallel iteration across the steps of high-order Runge-Kutta methods for nonstiff initial value problems, J. Comput. Appl. Math. 60, 309-329.

[29] Houwen, PJ. van der, Sommeijer, B.P. & Veen, W.A. van der [1994]: Parallelism across the steps in iterated Runge-Kutta methods for stiff initial value problems, Numerical Algorithms 8, 293-312.

[30] Houwen, PJ. van der & Swart, J.J.B. de [1995]: Triangularly implicit iteration methods for ODE-IVP solvers, Preprint NM-R9510, CWI, Amsterdam.

[31] Houwen, PJ. van der & Swart, J.J.B. de [1996]: Parallel block-triangular-implicit iteration of Runge-Kutta methods, in preparation.

[32] Houwen, PJ. van der & Veen, W.A. van der [1996]: Waveform relaxation methods for implicit differential equations, in preparation.

[33] Iserles, A. & N0rsett, S.P. [1990]: On the theory of parallel Runge-Kutta methods, IMA J. Numer. Anal. 10, 463-488.

[34] Jackson, K.R. & N0rsett, S.P. [1995]: The potential for parallelism in Runge-Kutta methods. Part 1: RK formulas in standard form, SIAM J. Numer. Anal. 32, 49-82.

[35] Leimkuhler, B. & Ruehli, A.E. [1993]: Rapid convergence of waveform relaxation, Appl. Numer. Math. 11,211-224.

[36] Lelarasmee, E. [1982], The waveform relaxation method for the time domain analysis of large scale nonlinear dynamical systems, PhD thesis, Univ. of California, Berkeley.

[37] Lelarasmee, E., Ruehli, A.E. & Sangiovanni-Vincentelli, A.L. [1982], The waveform relaxation method for time domain analysis of large scale integrated circuits, IEEE Trans. CAD IC Syst. 1, 131-145.

[38] Lie, I. [1987]: Some aspects of parallel Runge-Kutta methods, Report No. 3/87, Division Numerical Mathematics, University of Trondheim.

[39] Lioen,W.M. [1996]: On the diagonal approximation of full matrices, to appear in J. Comput. Appl. Math.

[40] Miranker, W.L. & Liniger, W. [1967]: Parallel methods for the numerical integration of ordinary differential equations, Math. Comp. 21, 303-320.

[41] Nevanlinna, O. [1985]: Matrix valued versions of a result of von Neumann with an application to time discretization, J. Comput. Appl. Math. 12 & 13, 475-489.

[42] N0rsett, S.P. [1974]: Semi-explicit Runge-Kutta methods, Report Mathematics and Computation No.6/74, Depart, of Mathematics, University of Trondheim.

[43] N0rsett, S.P. [1976]: Runge-Kutta methods with a multiple real eigenvalue only, BIT 16, 388- 393.

[44] N0rsett, S.P. & Simonsen, H.H. [1989]: Aspects of parallel Runge-Kutta methods, in: Numerical methods for ordinary differential equations, A. Bellen, C.W. Gear & E. Russo (eds.), Proceedings L'Aquila 1987, Lecture Notes in Mathematics 1386, Springer-Verlag, Berlin, 103-117.

[45] Orel, B. [1993]: Parallel Runge-Kutta methods with real eigenvalues, Appl. Numer. Math. 11, 241-250.

[46] Shampine, L.F. [1980]: Implementation of implicit formulas for the solution of ODEs, SIAM J. Sci. Stat. Comput. 1, 103-118.

[47] Sommeijer, B.P. [1993]: Parallelism in the numerical integration of initial value problems, CWI Tract 99, CWI, Amsterdam.

[48] Spijker, M.N. [1995]: The effect of the stopping of the Newton iteration in implicit linear multistep methods, Appl. Numer. Math. 18, 367-386.

[49] Veen, W.A. van der, Houwen, PJ. van der & Swart, J.J.B. de [1995]: Convergence aspects of step-parallel iteration of Runge-Kutta methods, Appl. Numer. Math. 18, 397'-411.

[50] Wolfbrandt, A. [1977]: A study of Rosenbrock processes with respect to order conditions and stiff stability, Ph. D. Thesis, Chalmers University of Technology, Goteborg.