Параллельные алгоритмы численного моделирования сложных динамических систем с сосредоточенными параметрами на основе неявных методов Рунге-Кутты

Автор: Назарова И.А.
Донецкий национальный технический университет
e-mail: nazarova@r5.donntu.ru
http://scg.donntu.ru/2005/scg_2005.pdf

Моделирование сложных динамических систем с сосредоточенными параметрами требует решения систем обыкновенных дифференциальных уравнений большой размерности (СОДУ). Эффективное решение таких систем возможно лишь с использованием высокопроизводительных параллельных вычислительных средств, как нового направления в области компьютерного моделирования [1-3]. В данной статье предлагается решение поставленной задачи в применении к одному конкретному классу методов интегрирования СОДУ, а именно неявным методам Рунге-Кутты, предназначенным для решения жестких задач.

Методы Рунге-Кутты с числом стадий равным s в общем виде определяются формулами (1) и (2):

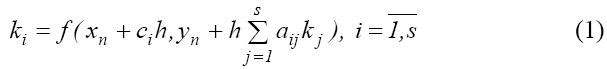
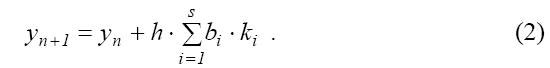
Коэффициенты a_i,j,c_i,b_i определяют уникальный вариант метода Рунге-Кутты и выбираются из соображений точности. Если a_i,j 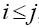= 0, при , то метод Рунге-Кутты является явным. В том случае, если a_i,j = 0 при 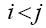(нижняя треугольная матрица), и хотя бы одно значение ,то k_i определяются неявно из уравнения:

такой метод называют диагонально неявным (ДНРК-метод).

Если в диагонально-неявном методе Рунге-Кутты все диагональные элементы одинаковы: , то такой метод называют однократно диагонально неявным (ОДНРК-метод). Во всех остальных случаях имеем полностью неявный метод Рунге-Кутты.

Для неявных методов шаговые коэффициенты k_i i=1,..,s, нельзя вычислить последовательно, так как (2) представляют собой систему уравнений, определяющих величины k_i неявным образом. Для полностью неявных методов РК все m • s неизвестных должны определяться одновременно, что существенно усложняет задачу (всего шаговых коэффициентов s и размерность каждого вектора 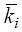равна m). В случае ДНРК имеем последовательность систем размерности m: для k₁, затем для k₂ и так далее.

Для системы из m ОДУ:

полностью неявный метод Рунге-Кутты (ПНМРК) имеет вид:

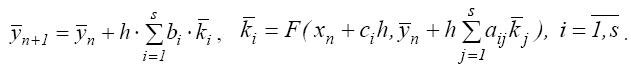
Рассмотрим параллельный алгоритм численного решения СОДУ полностью неявным методом Рунге-Кутты на основе квадратурных формул Радо и Лобатто[4]. Именно эти неявные методы имеют оптимальное сочетание характеристик устойчивости и точности. Так например, s-стадийный метод РадоIA имеет порядок практически в 2 раза больше, чем число стадий и обладает A-устойчивостью.

Применение полностью неявного метода Рунге-Куты требует определения шаговых 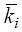,i=1,..,s, коэффициентов, которые связаны системой нелинейных уравнений. Для решения такой системы используем метод последовательных итераций:

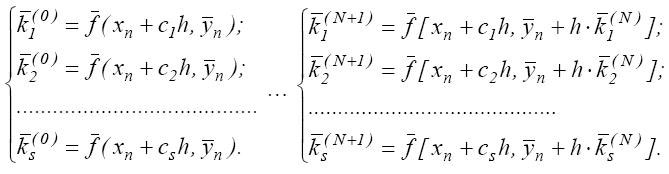
Анализ эффективности полученных параллельных алгоритмов производился на основе следующих показателей:

• время решения при помощи последовательного алгоритма;
• время решения при помощи параллельного алгоритма без учета и с учетом обменных операций (потенциальный и реальный параллелизм);
• анализ коммуникационной сложности алгоритма в зависимости от выбранной топологии соединения процессоров и модели передачи данных;
• коэффициенты ускорения, K_уск и эффективности, Е параллельного алгоритма;
• масштабируемость алгоритма на основе функции изоэффективности.

Вычислительные схемы параллельных алгоритмов получены с помощью аппарата графов влияния путем отыскания максимально-независимого множества вершин на минимальном остове[5].

Для неявных методов Рунге-Кутты время интегрирования в основном определяется числом обращений к функции правой части уравнения (1) и соотношением между временем вычисления функции f и флопом. Проведенные эксперименты показали, что для сложных функций правой части (1)(время вычисления функции T_f значительно превышает время одного флопа) коэффициент ускорения практически равен числу процессоров, а коэффициент эффективности — единице:

Для оценки времени выполнения операции передачи одного сообщения объемом n байт между двумя задачами локализованными на различных процессорах ("точка-точка") при распределенной памяти использовалась следующая модель[6-7]:

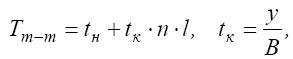
где t_н — латентность, длительность подготовки сообщения для передачи; l — длина маршрута; t_к— время передачи одного байта; у — число байт в слове; B — пропускная способность канала передачи данных (байт/секунда). Эта модель подразумевает использование способа передачи неделимых блоков информации, т.е. сообщений, поскольку объемы пересылаемых данных невелики (слово или 4 байта).

При реализации параллельных алгоритмов исследовались топологии: линейка/кольцо, решетка/тор и гиперкуб и оптимальные алгоритмы покоординатной маршрутизации. Выбор оптимальной топологии производился при анализе множества характеристик T_обм, T_выч, Z, K_уск, E, как некоторых функций 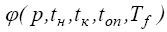на основе так называемой функции изоэффективности [8], позволяющей исследовать масштабируемость параллельного алгоритма. Определе¬ние характеристик параллелизма осуществлялось с помощью пакета Mathematica(Wolfram Research Inc.).

Численный эксперимент и проведенный сравнительный анализ динамических характеристик параллельных алгоритмов на основе неявных методов Рунге-Кутты показал, что достаточно большая по сравнению с явными методами вычислительная сложность этих методов не является препятствием для использования их в высокопроизводительных мультипроцессорных системах. Однако требуется тщательный учет всех составляющих параллельной системы для того, чтобы такое решение было масштабируемым и эффективным. В частности практически линейное ускорение и близкая к единичной эффективность достигаются при использовании синхроннной передачи данных в топологии гиперкуб.

1. Houwen P.J., Sommeijer B.P. Parallel ODE solver. // Proceedings of the International Conference on Supercomputing. — ACM Press, 2001, p.71-81.
2. Jackson K.R., Norsett S.P. The potential for parallelism in Runge-Kutta methods.Part 1: R-K formulas in standard form, SIAM J.Numer. Anal. 32,2001, p.49-82.
3. Houwen P.J., Sommeijer B.P. CWI Contribution to the development of parallel Runge-Kutta methods, Preprint NM- R9506, CWI, Amsterdam, 2003.
4. Хайрер Э., Ваннер Г. Решение обыкновенных дифференциальных уравнений. Жесткие и дифференциально-алгебраические задачи: Пер. с англ. — М.: Мир, 1999. —685с.
5. Воеводин В.В., Воеводин Вл.В. Параллельные вычисления. — СПб.: БХВ-Петербург, 2002. — 608с.
6. Foster I. Designing and Building Parallel Programs. — Addison-Wesley, 1999. — 302 с.
7. Немнюгин С.А., Стесик О.Л. Параллельное программирование для многопроцессорных ВС. — СПб.: БХВ-Петербург, 2002. — 400с.
8. Kumar V., Gupta A. Analyzing scalability of parallel algorithms and architectures.//Journal of Parallel and Distributed Computing.,22(3), 1994, p.379-391.