ПАРАЛЛЕЛЬНЫЕ АЛГОРИТМЫ ЧИСЛЕННОГО РЕШЕНИЯ СИСТЕМ ЛИНЕЙНЫХ ОБЫКНОВЕННЫХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ

Автор: Фельдман Л.П.
Донецкий национальный технический университет
e-mail: feldman@pmi.donntu.ru
http://www.imamod.ru/magazin/pdf/12/1206-015r.pdf

Введение

Моделирование сложных динамических систем с сосредоточенными параметрами требует обычно решения систем обыкновенных дифференциальных уравнений высокого порядка. Сокращение времени решения и, следовательно времени моделирования, возможно при использовании мультипроцессорных систем, эффективность работы которых существенно зависит от характеристик применяемых параллельных алгоритмов. Численное решение задачи Коши для системы линейных обыкновенных дифференциальных уравнений с постоянными коэффициентами

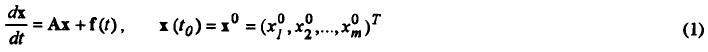
можно найти с помощью, например, формулы Рунге-Кутгы

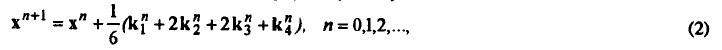
где

- выбранный шаг интегрирования.

Ниже рассматриваются алгоритмы распараллеливания вычислений, определяемых формулами (2), на процессорах SIMD структуры при использовании квадратной сетки, содержащей т*т процессорных элементов (ПЭ). На такой сетке эффективно выполняются матричные операции.

Алгоритм параллельного моделирования систем однородных уравнений

На выбранной сетке сложение двух матриц выполняется за время t_сл сложения двух чисел в каждом из ПЭ. Умножение двух матриц по систолическому алгоритму требует предварительного косого сдвига левого сомножителя по строкам и правого - по столбцам. На это требуется 2(m-1) одиночных сдвигов. Затем надо выполнить m умножений, m-1 сложений поэлементно и m-1 одиночный сдвиг. Таким образом, умножение двух матриц выполняется за время, равное

Вычисление компонент вектора у=Ах, равного произведению матрицы и вектора, мо¬жет быть выполнено по систолическому алгоритму. Вначале матрицу А сдвигают косо по строкам влево так, что элементы j-й строки сдвигаются циклически влево на j-1 позицию. На этом этапе требуется m-1 одиночных сдвигов. Заменим вектор х матрицей X такой, что каждый последующий столбец, начиная со второго, получается циклическим сдвигом предыдущего столбца на одну позицию вверх. На это потребуется m-1 сдвиг на заполнение матрицы X вектором х в m-1 одиночных сдвигов для косого сдвига этой же матрицы. Теперь, если перемножить поэлементно оба массива А_L*Х_R,

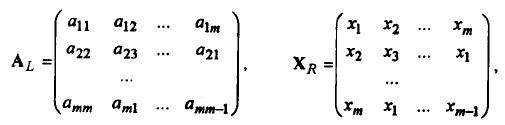
то получим следующий массив А_L*Х_R,

в котором сумма элементов i-й строки равна i-й компоненте у_i, вычисляемого вектора. Все компоненты вектора у вычислим параллельно по алгоритму сдваивания. Сначала попарно сложим соседние элементы в каждой из строк, затем опять попарно сложим полученные значения, отстоящие друг от друга на две позиции, и так до тех пор, пока в каждой из строк все ее элементы станут равными вычисляемому значению соответствующей компоненты вектора у. Этот процесс потребует log₂m (берем ближайшее наибольшее целое к этому числу, равное 1) сложений и столько же сдвигов. Если учесть, что сдвиги выполняются соответственно на 1, 2,2²,...,2^l-1 позиций, то общее число одиночных сдвигов равно N_сдв=2ⁱ-1=m. Время, затрачиваемое на вычисление компонент вектора у, может быть выражено следующей формулой:

В формуле (4) первое слагаемое определяет время косого сдвига матрицы X, а последнее - время сдвигов при сложении по алгоритму сдваивания по строкам. Времена косого сдвига матрицы А и заполнения матрицы X не вошли в (4), так как эти операции являются подготовительными и выполняются только один раз в начале решения основной задачи. Приведем другой алгоритм вычисления компонент вектора у=Ах, в котором исходная матрица А транспонируется, а матрица X формируется из вектора х по столбцам без сдвигов. Если перемножить поэлементно оба массива А_T*Х, то получим (5). В соответствии с методом Рунге-Кутты (2), каждый следующий шаг состоит в повторении умножения исходной матрицы А на вектор, полученный на предыдущем шаге. Поэтому для продолжения решения полученную матрицу, каждая строка которой равна вектору у^T, необходимо транспонировать:

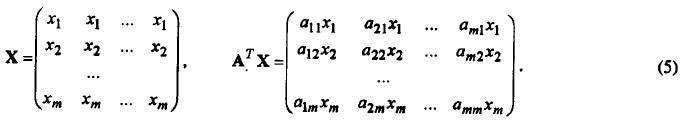
Матрицу можно транспонировать, если сделать вначале косой сдвиг влево по строкам, а затем косой сдвиг вниз по столбцам. В первом алгоритме требовался только один косой сдвиг матрицы по столбцам, откуда следует, что он менее трудоемок.

Вычисление значения вектора неизвестных xⁿ⁺¹ по формуле (2) требует предварительного определения значений k_i, 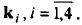Эти векторы, как это следует из формул (2), должны вычисляться последовательно. Перепишем их для однородной системы в виде, удобном для оценки времени выполнения вычислений

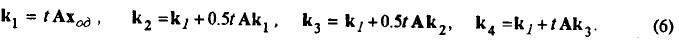
При вычислении каждого k_i, необходимо умножить матрицу на вектор и сложить с другим вектором, поэтому используя (4), получим для времени вычисления всех k_i, формулу

Теперь можно определить время, необходимое для выполнения вычислений на одном шаге T_n=T_k+t_yмн+4t_сл. Время решения задачи, содержащей N шагов, будет равно T_RK=t_cдв(m-l)+NT_n. Здесь первое слагаемое учитывает время подготовительных операций при начальном косом сдвиге матрицы А. Если подставить найденные выше значения, то последнюю формулу можно будет записать в виде

В последней формуле явно выделены полные времена, затрачиваемые на каждый вид операций, за N тактов решения задачи. Значительная часть времени затрачивается на выполнение сдвигов. Если принять, для простоты оценки, что t_умн=t_сл и обозначить через z=t_сдв/t_yмн то приводимый на рис.1 график (точки обозначены знаком *) зависимости отношения времени сдвигов ко времени арифметических операций при z=0.1 от порядка решаемой системы m показывает, что на выполнение сдвигов затрачивается значительно больше времени, чем на вычисления.

Так для системы сотого порядка это отношение равно 2, а для системы, порядок которой равен 1000, это отношение равно 14. При решении систем высокого порядка, несмотря на массовый обмен данными, реализованный в системах SIMD, он определяет время решения задачи, ограничивая вычислительные возможности системы.

Рассмотрим алгоритм, который имеет меньшее число сдвигов. Для этого выразим на очередном шаге полный оператор, позволяющий определить значение вектора неизвестных на следующем шаге. Назовем его оператором (матрицей) перехода. Используя формулы (б), выразим k_i для через k_i подставим найденные выражения в (2), получим для однородной системы

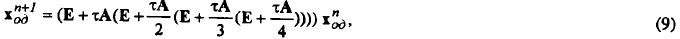
где Е - единичная матрица.

Матрицу перехода следует определить один раз до выполнения вычислений по формуле (9). На это потребуется три умножения матриц на скаляр, четыре последовательных сложения полученных матриц с единичной матрицей и три матричных умножения. Умножение матриц будем выполнять по систолическому алгоритму, учитывая, что в каждом из трех матричных произведений используется один и тот же левый сомножитель, равный А. Время, затраченное на выполнение предварительных операций вычисления матрицы перехода, представляется следующей формулой Т_подг=3T_sys+4t_сп+3t_умн.

Теперь для вычисления искомого вектора хⁿ⁺¹ надо умножить матрицу перехода на вектор хⁿ, что потребует, в соответствии с (4), времени равного Т_у. Общее время решения задачи по рассмотренному алгоритму составит .

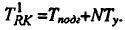Подставив выражения для входящих сюда Т_подг и T_y, получим окончательно

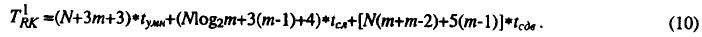
Сравнивая с (8) можно заключить, что хотя время выполнения подготовительных операций этого алгоритма больше времени алгоритма, рассмотренного выше, однако при больших m и N это не имеет существенного значения, так как доля их в общем объеме вычислений пренебрежимо мала. Существенным здесь является то, что в общем объеме вычислений в последнем алгоритме число сдвигов в 4 раза меньше в сравнении с первым алгоритмом. Потому он будет решать задачу быстрее не менее чем в четыре раза. Для второго алгоритма также характерным является то, что на выполнение сдвигов затрачивается значительно больше времени, чем на вычисления (точки обозначены на графике знаком +).

Время выполнения всех N тактов решения задачи по методу Рунге-Кутты на однопроцессорном компьютере может быть определено по формуле

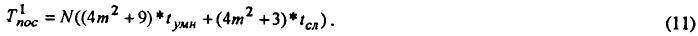
Ускорение первого из рассмотренных выше алгоритмов использующего m² процессоров, выражается следующей формулой:

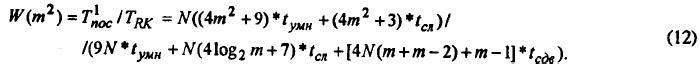
Из нее следует, что ускорение от N практически не зависит. При больших m асимптотическое значение ускорения равно W(m²)=10m. Аналогично определяется ускорение для второго алгоритма

Ускорение второго алгоритма приблизительно в четыре раза больше первого. Асимптотическое значение ускорения второго алгоритма равно W¹(m²)=10m.

Чтобы оценить потенциальный параллелизм алгоритма, его ускорение определяют обычно не учитывая время сдвигов. В нашем случае для второго алгоритма (13) получим

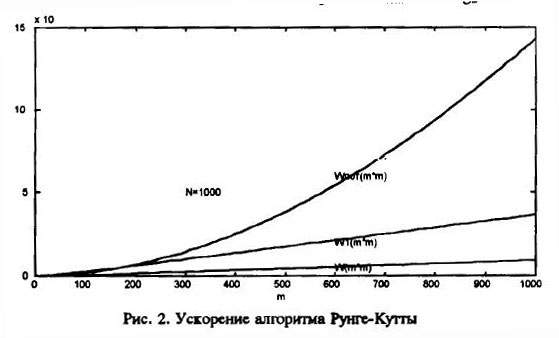
Ниже приведены для сравнения графики ускорений для параллельного алгоритма без учета времени на сдвиги W_пот первого и второго параллельных алгоритмов (12) и (14). Асимптотическое значение для потенциального алгоритма равно W_пот=8m²/log₂m.

2. Алгоритм параллельного моделирования систем неоднородных уравнений

При решении неоднородной системы уравнений по формуле Рунге-Кутты (2) необходимо, дополнительно к рассмотренным выше расчетам по формулам (6), вычислить на каждом шаге n также и значения всех функций f_i(t) в трех точках. В общем случае все эти функции могут быть различными, поэтому одновременное параллельное их вычисление на SIMD процессоре невозможно. Однако расчет значений одной, любой из них, может быть выполнен параллельно для всех значений аргумента t_n,t_n+0.5, 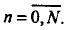Поскольку для произвольной функции f_i(t) нельзя определить возможность распараллеливания вычислений ее значения для заданного значения аргумента, то обозначим через 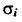, время последовательного расчета ее значения для одного значения аргумента на ПЭ. Вычисления таблицы значений всех функций f_i(t) для всех 2N значений аргумента t потребует на линейке из 2N ПЭ времени, равного сумме всех 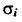, так как функции вычисляются последовательно. Эти вычисления выполняются до начала решения задачи по формулам (2). Если ПЭ достаточно, то для каждой функции можно выделить свою линейку. Затем на сетке m*m ПЭ сформируем из полученной таблицы значений функций f_iⁿ матрицу F(п), элементы F_ij(n) которой являются линейным массивом длины 2N. Все элементы i-й строки матрицы одинаковы и равны значению i-й функции f_iⁿ для t=t_n, т.е. f_iⁿ=F_ij(n). На эти преобразования потребуется порядка 2N одиночных сдвигов. Теперь можно перейти к вычислениям искомого решения по формулам (2), подобно тому, как это делалось при решении однородной системы. Время расчетов решения неоднородной системы на очередном шаге n будет отличаться от времени решения соответствующей однородной системы на время трех матричных сложений. Учитывая время выполнения подготовительных операций, получим для времени решения неоднородной задачи за N шагов следующую формулу:

где T_RK определяется формулой (8). Выполнение алгоритма, определяемого формулами (2), на однопроцессорном компьютере потребует времени, равного

Заключение

Оценим влияние времени вычисления значений функций f_i(t) в зависимости от их сложности на время решения задачи. Ниже приведен график отношения времен решения неоднородной и однородной систем дифференциальных уравнений в зависимости от сложности вычисления функций f_i(t).

Для расчетов было принято, что все f_i(t) имеют одинаковую сложность, которая выражается числом операций, равным k для каждой функции. Из графиков видно, что рассмотренный выше алгоритм предварительного параллельного расчета функций f_i(t) незначительно увеличивает время решения неоднородной системы по сравнению со временем решения однородной системы. Таким образом, предложенные алгоритмы позволяют существенно ускорить процесс моделирования.

СПИСОК ЛИТЕРАТУРЫ

1. Самарский А.А., Гулин А.В. Численные методы. - М.:Наука, 1989.

2. Фельдман Л.П., Труб ИМ. Эффективность параллельных алгоритмов численного решения краевых задач с частными производными при их реализации на SIMD компьютерах. Информатика, кибернетика и вычислительная техника. Сб. Научн. Тр. Донецкого государственного технического университета. Вып. 1; Донецк: ДонГТУ, 1997, с. 26-34.