ЭФФЕКТИВНЫЕ МЕТОДЫ РАСПАРАЛЛЕЛИВАНИЯ ЧИСЛЕННОГО РЕШЕНИЯ ЗАДАЧИ КОШИ ДЛЯ ОБЫКНОВЕННЫХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ

Авторы: Фельдман Л.П., Дмитриева O.А.
Донецкий национальный технический университет
83000, Донецк, ул. Артема, 58
e-mail: feldman@pmi.donntu.ru, dmitriv@r5.donntu.ru
http://www.imamod.ru/magazin/pdf/13/1307-066r.pdf

Введение

В последнее время появилось большое количество численных методов интегрирования дифференциальных уравнений, которые ориентированы на вычислительные системы с параллельной архитектурой. Однако практическое использование большинства методов не всегда оправдано, поскольку многие из них либо обладают численной неустойчивостью, либо имеют очень сложную структуру, приводящую к потере эффективности. К методам, лишенным указанных недостатков, можно отнести блочные. Блочным будем называть метод, при котором для блока из к точек новые к значений функции вычисляются одновременно [1]. Эта особенность методов, во-первых, согласуется с архитектурой параллельных вычислительных систем, а, во-вторых, позволяет вычислять коэффициенты разностных формул не в процессе интегрирова¬ния, а на этапе разработки метода, что значительно увеличивает эффективность счета. В то же время для этих методов отсутствуют оценки погрешностей и условия сходимости. Поэтому данная статья посвящена исследованию сходимости и получению оценок погрешностей параллельных блочных методов решения задачи Коши для обыкновенных дифференциальных уравнений

Численное решение задачи Кош и блочными методами

Рассмотрим решение задачи Коши

к точечным блочным разностным методом. Множество M точек равномерной сетки t_m m=1,2,...,M и t_M=T шагом тразобьем на блоки, содержащие по к точек, kN=M. В каждом блоке введем номер точки i=0,1,...,k и обозначим через t_n,i точку n-го блока с номером i. Точку t_n,0 назовем началом блока n, a t_n,k - концом блока. Очевидно, что имеет место t_n,k=t_n+1,0. Условимся начальную точку в блок не включать.

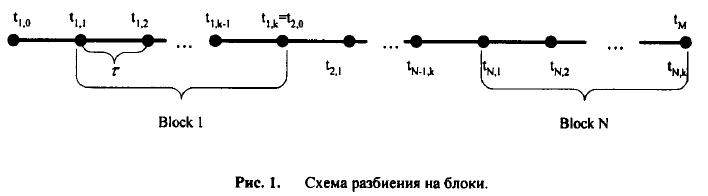
Если для расчета значений в новом блоке используется только последняя точка предшествующего - будем говорить об одношаговых, а если все точки предшествующего блока - многошаговых блочных методах

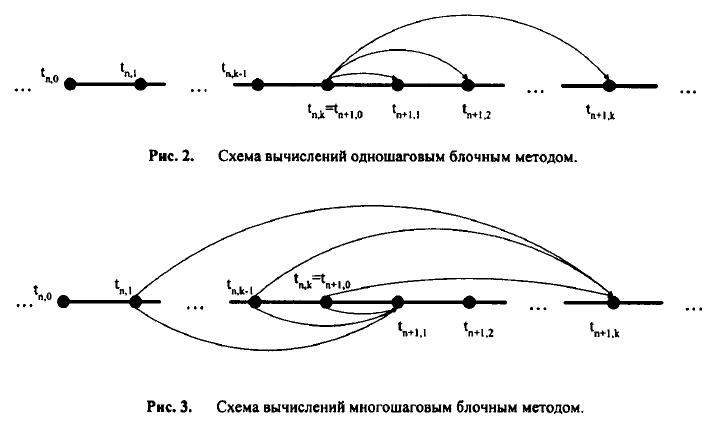
В общем случае уравнения многошаговых разностных методов для блока из к точек с учетом введенных обозначений можно записать в виде

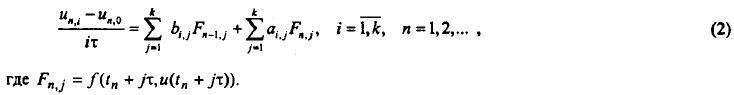
Для одношаговых разностных методов уравнения могут быть представлены как

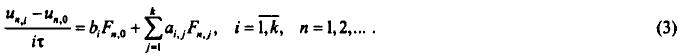
Погрешность аппроксимации блочных методов

Выражение для погрешности аппроксимации рассматриваемого разностного метода (2) на решении уравнения (1) имеет вид

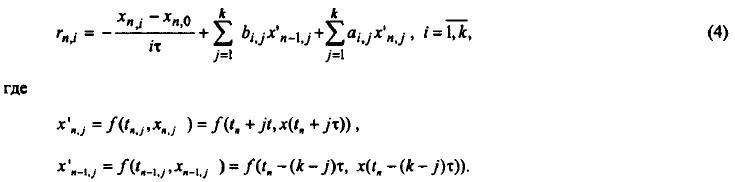
После разложения x_n,i, x_n,j^' и x_n-1,j^' в ряды Тейлора в окрестности точки t_n получим

Отсюда следует, что погрешность аппроксимации имеет порядок р, если выполнены условия

Система уравнений (6) для каждого фиксированного i содержит р уравнений и 2к неизвестных b_i,1,b_i,2,...,b_i,k,a_i,1,a_i,2,...,a_i,k. Потребуем, чтобы р=2k, тогда из системы (6) можно будет определить все неизвестные коэффициенты. Таким образом, наивысший порядок аппроксимации многошагового k-точечного блочного метода равен 2к. Его погрешность в соответствии с (5) определяется формулой

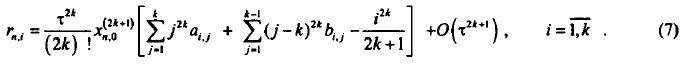
Для одношаговых блочных методов аппроксимацию порядка р обеспечивают следующие условия:

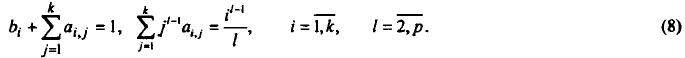
Система уравнений (8) для каждого фиксированного i содержит p уравнений и k+1 неизвестных b_i,a_i,1,a_i,2,...,a_i,k. Если потребовать, чтобы р=k+1, тогда из системы (8) можно будет определить все неизвестные коэффициенты. Отсюда следует, что наивысший порядок аппроксимации одношагового k-точечного блочного метода равен k+1. Его погрешность определяется формулой

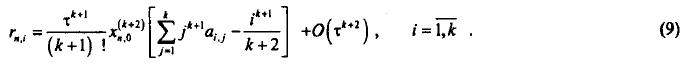
Элементы b_i,j и а_i,j,i,j=1,2,...,k матриц В и А соответственно можно найти в зависимости от выбранного метода, решая системы (6) или (8) для конкретной размерности блока k.

Сходимость и оценка погрешности многошаговых блочных методов

Обозначим через u_n - вектор значений приближенного решения в точках n-го блока с компонентами u_n,i, i=1,2,...k и через u_n^' вектор, компоненты которого u_n,i^' = f(t_n,i,u_n,i)=F_n,i, и u_n-1,i^' = f(t_n-1,i,u_n-1,i)= F_n-1,i равны значениям правых частей уравнения (1) в точках, соответствующих значениям приближенного решения. Запишем систему (2) в векторной форме

где D =(d_i,j) - диагональная матрица с элементами d_u=i, i=1,2,...,k, e - единичный вектор столбец, В и А - матрицы размерности k*k с компонентами b_i,j и a_i,j соответственно, i=1,2....,k, у=1,2,..,k.

Обозначим через х_n - вектор значений точного решения задачи (1) в точках блока n. Получим уравнение, которому удовлетворяет вектор погрешностей в блоке z_n = u_n - x_n. Подставим в левую часть уравнения (10) выражение u_n = z_n + x_n, добавим к правой части и вычтем из нее Bx_n-1^' + Ах_n^', тогда уравнение для погрешности примет вид

Входящее в правую часть выражение

представляет собой вектор невязок разностных уравнений (2) на точном решении уравнения (1). Поскольку разностные уравнения (10) аппроксимируют исходное уравнение в точках блока с порядком 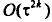, то имеет место оценка

Оставшиеся члены правой части уравнения для погрешности обозначим через

Тогда уравнение для погрешности запишется короче

Вектор функция w_n от погрешности z_n зависит нелинейно. Вид этой зависимости определяется функцией f(t,x). В дальнейшем будем предполагать, что f(t,x) удовлетворяет условию Липшица по второму аргументу, т. е.

для всех t, x₁, x₂ из рассматриваемой области. Согласно формуле конечных приращений Лагранжа для компоненты i имеем

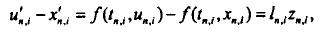
где

Подставляя последние в (13), получим

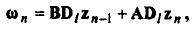
где D_l - диагональная матрица с элементами d_l,i^l =l_n,i, i=1,2,...,k, и ее норма имеет в силу (12) следующую оценку:

Заменим w_n в уравнении (14) полученным для него выражением

Введем нормы

Далее, учитывая (12), (16) и то, что ПОЛУЧИМ неравенство

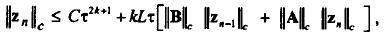
которое преобразуем к виду

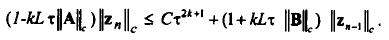
Если на наложить ограничение

то оценка, связывающая нормы погрешностей соседних блоков примет вид

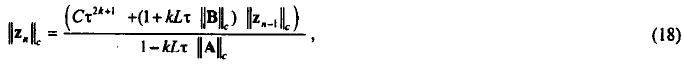
так как в силу условия (17) имеет место 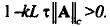. Подставляя последовательно в (18) значения погрешностей для блоков n-1,n-2,...,1, послеупрощения получим

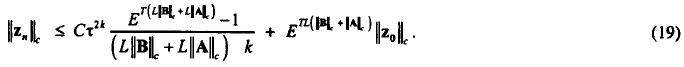
Таким образом, доказана

Теорема. Пусть правая часть уравнения (1) f(t,y) удовлетворяет условию Липшица по второму аргументу с константой L и г_n - невязка многошагового k-точечного блочного метода (2), определенная согласно (3) с оценкой (12). Тогда при

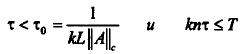
для погрешности метода имеет место оценка (19).

Следствие. Если разностное уравнение (2) аппроксимирует исходное уравнение (1), то решение разностной задачи (2) сходится при —> 0 к решению исходной задачи (1), причем порядок точности совпадает с порядком аппроксимации.

После проведения соответствующих преобразований можно получить оценку погрешности одношаговых блочных методов. При тех же ограничениях на длину шага она будет иметь следующий вид:

Алгоритм параллельного решения нелинейной разностной задачи

Для вычисления приближенных значений задачи Коши (1) необходимо решить нелинейную систему уравнений (2). Используем для этого следующий итерационный процесс

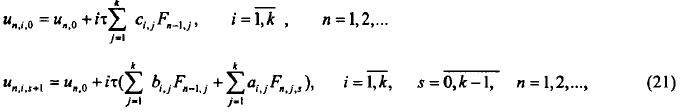
который позволяет проводить вычисления параллельно для каждого узла блока. После выпол¬нения k шагов вычислений по формулам (21) локальная ошибка в узлах блока будет иметь порядок Поскольку разностные уравнения (2) аппроксимируют дифференциальное уравнение (1) с порядком , дальнейшие шаги не дадут повышения порядка точности результатов. Формулы итерационного процесса для одношаговых блочных методов

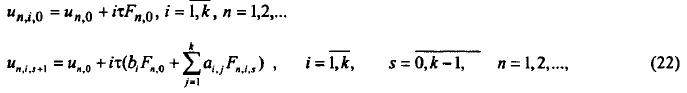
Сравнительные характеристики численного решения тестовых задач

Выберем в качестве иллюстрации решения блочными методами умеренно устойчивую задачу [2]

решение которой многозначным методом приводит к значительным вычислительным погрешностям. Аналитическое решение рассматриваемой задачи имеет вид

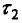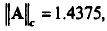
Найдем решение задачи (23) одношаговым (с размерностью блока к=4), многошаговым (с блоками 4x4) блочными методами и методом Ньютона (с размерностью блоков 4x4). Шаги интегрирования для метода (2) и для метода (3) выберем из условия (17). Решение выполним в системе Mathematica. Для одношагового четырехточечного метода 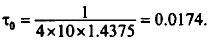Для многошагового четырехточечного метода Шаг для метода Ньютона выберем таким же, как и для многошагового метода. Поскольку точное решение (24) известно, то по результатам приближенного решения можно оценить максимальную ошибку, которая всеми методами достигается в точке t= 1. Сведем полученные результаты решения в таблицу, характеризующую зависимость ошибки от числа выполненных итераций.

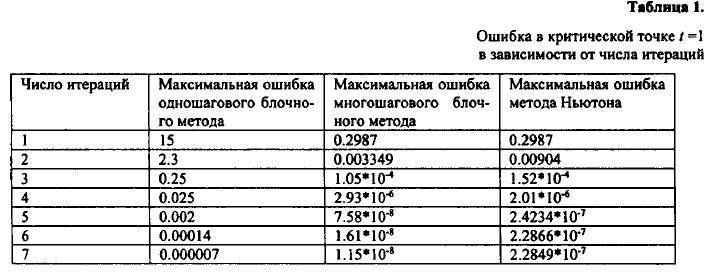
Решение тестовых задач показало, что многошаговые блочные методы превосходят по точности решения известные методы Ньютона, а по такому показателю как трудоемкость, они требуют значительно меньшего числа операций.

Для параллельного выполнения вычислений по формулам (21) и (22) использовалась вычислительная система SIMD структуры с линейкой процессорных элементов [3] размерности k. Если учитывать только время вычислений правой части уравнений, т.к. времена выполнения арифметических операций и обмена значительно меньше времени вычисления правой части, то ускорение k-точечного многошагового параллельного алгоритма можно считать приближенно равным 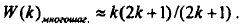Для параллельного одношагового k-точечного алгоритма эта характеристика будет выглядеть как В качестве еще одной оценки степени параллелизма алгоритма использовался коэффициент эффективности, который определяется отношением ускорения к числу используемых процессорных элементов. Нетрудно видеть, что для двух типов рассмотренных в статье блочных методов этот коэффициент близок к единице.

1. Системы параллельной обработки: Пер. с англ. / Под. ред. Ивенса Д. - М.: Мир,1985, 416с.

2. Каханер Д.-, Моулер К.Нэш С. Численные методы и математическое обеспечение: Пер. с англ. - М.: Мир, 1998, 575 с.

3. Дмитриева О.А. Анализ параллельных алгоритмов численного решения систем обыкновенных диффе¬ ренциальных уравнений методами Адамса-Башфорта и Адамса-Моултона. // Математическое модели¬ рование. 2000, т. 12, № 5, с. 81-86.