RUS | UKR | ENG || ДонНТУ> Портал магістрів ДонНТУ

Фiрсова Алiса Олександрiвна

Факультет обчислювальної технiки та iнформатики

Кафедра прикладної математики та iнформатики

Спецiальнiсть: Економiчна кiбернетика

Тема випускноi роботи:

Моделювання динамiчних систем в економiцi

Науковий керывник: Дмитрієва Ольга Анатолієвна

ДонНТУ> Портал магістрів ДонНТУ| Автобіографія |

Автореферат

Актуальність

Протягом останніх років політика державного реформування соціально-економічних відносин в Україні орієнтувалася на макроекономічну стабілізацію. Значимість ефективного керування на мікрорівні недооцінювалась. Це багато в чому сприяло кризовим явищам у соціальній сфері країни, зниженню рівня добробуту населення. Виникла необхідність у перегляді шляхів і методів перетворень на мікрорівні  - рівні окремих підприємств, що формують основу сучасної економіки. Багато підприємств як і раніше зазнають труднощів, пов'язаних з падінням обсягів виробництва й рентабельності продажу, втратою традиційних ринків збуту продукції й труднощами в пошуку нових, слабкою узгодженістю в діях вищої ланки керування, відсутністю чітко виражених напрямків розвитку, недостатністю освоєння нових видів продукції й нових технологій керування. Подолання цих труднощів здійснюється в основному інтуїтивно, без опори на науково обґрунтовані системи підтримки прийняття рішень, і носить що формально-констатуючий, а не попереджуючий характер.

При такому підході складно не тільки об'єктивно оцінювати стан управлінського процесу, але й визначати тенденції його розвитку й вносити в нього необхідні корективи. Виникає протиріччя між мінливим змістом господарської діяльності й відстаючої по темпах удосконалювання керуванням на підприємствах. [1]

У ході розвитку ринкових відносин об'єктивно позначилася потреба у формуванні нового економіко-математичного апарата й нового інструментарію, як для аналізу економічної динаміки, так і для розробки стратегій керування економічними процесами. [2]

Математичне моделювання відіграє величезну роль у завданнях економічного планування й прогнозування. Це обумовлюється, у першу чергу, принциповою неможливістю експериментів в економіці й важливістю відповідних завдань. Існуючі концепції найчастіше досить по-різному оцінюють факти й при різному трактуванні важко вирішити, який теоретичний підхід найбільш  правильний. При цьому, виходячи із самого характеру економічної науки, неможливо однозначно доказово перевірити ці теоретичні вишукування. І хоча зрозуміло, що реальна економічна діяльність підприємства не може бути повністю описана ніякою, навіть самою завбачливою моделлю, проте, необхідне правильне розміщення акцентів при формалізації.  Крім цього багато економічних систем мають довгострокову пам'ять, тобто поведінка системи, при t>t₀, визначається не тільки набором визначальних її параметрів у цей момент часу, але й динамікою їхніх змін у попередні. [3] У зв'язку з цим необхідно мати кількісні методи, що дозволяють виявляти динаміку процесів на ринку, фактори, що роблять вплив на формування показників цього ринку, у тому числі з урахуванням специфіки економіки України. [4] Тому тема магістерської роботи є актуальною й практично значимою.

Мета й завдання

Мета - розробити динамічну модель економічної системи, що адекватно реагує на умови, що змінюються, у країні.

Завдання:

• виявити фактори, що впливають на економічний стан країни;

• вивчити поточний стан економіки;

•  розглянути методи, застосованні до даної системи й виявити найбільше практично цінні;

•  розробити динамічну систему, що максимально відповідає поточному стану економіки.

Огляд досліджень і розробок по темі

   У ДонНТУ моделюванням динамічних систем в економіці займаються Дмитрієва О. А. і Смирнов А. В. Також цією проблемою займаються журнал «Проблеми керування й інформатики» за підтримкою Національної академії наук України, Інститут кібернетики ім. В.М. Глушкова НАН Україини,  Інститут космічних досліджувань НАН України и НКА України [5]. Київський національний університет імені Тараса Шевченко, Інститут механіки, Інститут математики, Український національний комітет з теоретичній і прикладній механіці [6]. Журнал «Сучасні наукомісткі технології», Ставропольський технологічний інститут сервісу [7]. Петрозаводський державний університет, кафедра математичного моделювання систем керування [8]. Алтайський державний університет [9] й др.

Наукова новизна

Наукова новизна:

•  застосовані робастні алгоритми еліпсоїдального оцінювання стану нелінійних динамічних систем в економіці;

• розроблено математичну модель, що реагує на зміни в економіці.

Теоретичні дані даної магістерської роботи можуть знайти застосування в будь-якій сфері економіки й не тільки для оцінювання стану динамічних систем і для оптимального керування ними, а також можуть слугувати стратегією для керування економікою.

 Головна ідея роботи

Постановка завдання. Нехай еволюція в часі дискретної динамічної системи (ДС) і її каналу виміру описується рівняннями

x_k+1 = A_kx_k + f_k(u_k),      (1)

y_k = h_k^Tx_k + ξ_k.               (2)

            Тут k = 0, 1, …— дискретний час; x_k — недоступний безпосередній зміні n-мірний вектор стану, x_k Î Rⁿ; Rⁿ — n-мірне речовинний еквілідовий простір; u_k — відомий вектор керування, u_kÎ R^m, m ≤ n; y_k — вектор спостережуваних сигналів, що представляють собою результати виміру виходу об'єкта h_k^Tx_k, зашумленного дією аддитивної перешкоди ξ_k, yk = (y_1k,…,y_mk), ξ_k^T=(ξ_1k,…, ξ_mk); T—символ операції транспонування; A_k й hk=  — відомі матриці размерності n´ n й m´ n відповідно, det A_k ¹ 0 "k = 0, 1,…, h_ikÎRⁿ; f_k(u_k)— задана n-мірна функція. Передбачається, що перешкода ξ_k задовольняє обмеженням по компонентах або по норме

ξ_ik² ≤ c_ip², i = 1,…, m, k=0, 1, …, (3)

(ξ_ik–ξ_i,k-1)²≤c_ir², i=1,…, m, k=1, 2, …, (4)

ξ_kξ_k≤c_p², k=0, 1, …, (5)

(ξ_k–ξ_k-1)^T(ξ_k–ξ_k-1) ≤c_r², k=1, 2, …, (6)

де c_ip ,c_i, c_ir, c_r — задані константи.

            У припущенні, що результати поточних вимірів y_k, k = 0, 1, …, відомі, ставиться завдання еліпсоїдального оцінювання невідомого вектора стану x_k у вигляді

x_k Î E[  , H_k] = E_k ,

де E[  , H_k] ={x: σ(x, , H_k) ≤ 1}, σ(x, , H_k) = (x - )^TH_k^-1(x - ), — центр еліпсоїда, H_k = Hk > 0. Параметри апріорного еліпсоїда , H_k при k = 0 покладаються заданими.

            На ряді з дискретної ДС (1), (2) розглядається завдання еліпсоїдального оцінювання вектора стану x_k безперервної ДС

,              (8)

y_k = h_k^Tx_k + ξ_k                       (9)

по дискретних вимірах її виходу y_k = y(t_k) у моменти часу t = t_k, t_k+1=t_k+T, T — інтервал дискретності виміру й зміни керування. Тут t — безперервний час, t Î [0, ∞); x_k = x(t_k) і ξ_k = ξ (t_k) — недоступний безпосередньому виміру невідомий вектор стану й перешкода виміру; hk = h(t_k); C(t), D(t) — задані для всіх t ≥ 0 матриці відповідних розмірностей з обмеженими безперервними елементами. Інші припущення відповідають властивостям дискретної системи (1), (2).

            Оцінювання стану дискретних ДС. З рівнянь (1), (2) безпосередньо одержуємо

ξ_k = y_k - h_k^Tx_k  ,                (10)

ξ_k-1 = y_k-1 - h_k-1^Tx_k-1 .         (11)

            Скориставшись рівнянням (1), з (10) і (11) знаходимо

ξ_k - ξ_k-1 = z_k- r_k^Tx_k,           (12)

де

 z_k=(z_1k,…,z_mk)^T=y_k-y_k-1–h_k-1^TA_k-1^-1f_k-1(u_k-1), r_k^T= =h_k^T-h_k-1^TA_k-1^-1...

Запровадивши позначення ζ_k = ξ_k - ξ_k-1, співвідношення (12) формально можна представити як додатковий канал виміру системи (1)

z_k=r_k^Tx_k+ ζ_k,             (13)

де перешкода ζ_k = (ζ_1k, …, ζ_mk)^T задовольняє обмеженням по компонентах або по нормі

ζ_ik² ≤ c_ir², i = 1,…, m, k=1, 2, …, (14)

ζ_kζ_k≤c_r², k=0, 1, …, (15)

Досліджуємо випадок покомпонентного обмеження перешкод. Розглянемо множини

S_ip(x_k) = {x_k: (y_ik – h_ip^Tx_k)²≤c_ip², k = 0, 1,…, i=1, …m}, (16)

S_ir(x_k) ={x_k: (z_ik–r_ik^Tx_k)²≤c_ir², k=1, 2,…, i=1, …m}, (17)

            Співвідношення (16), (17) визначають у фазовому просторі системи (1), (2) множини S_ip(x_k) і S_ir(x_k) її станів, сумісні з результатами вимірів. Ці множини являють собою 2m гіперсмуг, кожна з яких обмежена двома попарно паралельними гіперплощинами y_ik-h_ik^Tx_k=±c_ir, i =1, …m...

            Очевидно, що для невідомого вектора стану системи (1), (2) x_k виконується включення x_k Î D(x_k), де D(x_k) – перетинання всіх 2m гіперсмуг множин (16), (17). При цьому, відповідно до припущення, виконується також включення (7). Тому виконується й включення x_k Î E[  ], де E[  ] – еліпсоїд виду (7) такий, що D(x_k)∩E[  ]Ì E[  ]. Для побудови еліпсоїда E[  ] доцільно скористатися робастним алгоритмом послідовної побудови 2m еліпсоїдів, що містять перетинання еліпсоїдів з гіперсмугами S_ip(x_k), i = 1, …m і S_ir(x_k), i = m+1, …, 2m... Ці еліпсоїди можна будувати за критерієм мінімуму визначника (багатомірного обсягу еліпсоїда) або сліду відповідних матриць , . Оцінюючий еліпсоїд , для якого гарантовано виконується включення x_k+1 Î , де x_k+1 – невідомий вектор стану системи (1), (2), являє собою образ еліпсоїда E[  ] при його лінійному відображенні в силу рівняння (1). Центр і матриця еліпсоїда  визначаються співвідношеннями , .

Для випадку (4) перешкода ξ_k і швидкість її зміни по нормі множини станів системи (1), (2), сумісні з результатами вимірів, обмежуються співвідношеннями

S_p(x_k)={x_k:(y_k – h_k^Tx_k)^T(y_k – h_k^Tx_k)≤c_p²,   (18)

S_r(x_k)={x_k:(z_k – r_k^Tx_k)^T(z_k – r_k^Tx_k)≤c_r²,   (19)

Ці множини являють собою циліндри у фазовому просторі Rⁿ системи (1), (2). Для її невідомого вектора стану виконується включення x_kÎD(x_k), де D(x_k)=S_p(x_k)∩S_r(x_k). Із припущення про виконання умови (7) безпосередньо треба включення x_kÎD(x_k)∩E[  ]. Тому оцінюючий еліпсоїд, гарантовано утримуючий невідомий вектор x_k, може бути побудований за допомогою еліпсоїдальної апроксимації перетинання E[  ] з множиною S_p(x_k) і потім апроксимації перетинання отриманого еліпсоїда з множиною S_r(x_k). При цьому оцінювання вектора стану системи (1), (2) зводиться до побудови параметричних сімейств еліпсоїдів  і  виду (7), що містять відповідно перетинання E[  ]∩S_p(x_k) і ∩S_r(x_k), де ν ≥ 0, τ ≥ 0 – параметри сімейств. Центр і матриця H_k+1 оцінюючого еліпсоїда, для якого гарантовано виконується включення x_k+1Î  , визначаються співвідношеннями , . Робастний алгоритм побудови сімейства еліпсоїдів  має вигляд

,                                 (20)

,     (21)

.                             (22)

Тут e_k=h_k^TH_kh_k, , , I_m – ­одинична матриця розмірності m´m, b_kÎ(0,1) і a_k >0 – параметри алгоритму. Центр  і матриця  еліпсоїда É  ÉS_r(x_k) обчислюються по формулах (20) – (22) із заміною в їхніх правих частинах величин n, H_k, c_p і  відповідно на величини τ, , , c_r й .

Оцінювання стану безперервних ДС. Для гарантованого еліпсоїдального оцінювання вектора стану x_k = x(t_k) системи (8), (9) у дискретні моменти часу t = t_k, що відповідають моменти виміру виходу y_k = y(t_k) і зміни вектора керування u_k = u(t_k), опишемо цю систему різницевими рівняннями виду (1), (2). Скориставшись формулами для рішення систем лінійних диференціальних рівнянь зі змінною матрицею, одержуємо

A_k = K(t_k+1,t_k), f_k(u_k)=B_ku_k,

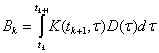
Тут K(t, t_k) - перехідна матриця (матриця Коші) системи (6) при  t≥t_k. Матриця K(t_k+1,t_k)=X(t, t_k) при t=t_k+1, де X(t, t_k) - рішення диференціального матричного рівняння з початковою умовою X(t_k, t_k)=I_n. Для випадку стаціонарної системи (8)

A_k≡A=exp{CT}, B_k≡B= 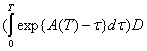 . [10, 11]

Результати роботи

На даному етапі розробки магістерської роботи був проведений аналіз поточного стану економіки, що підтвердив необхідність застосування методів математичного моделювання. При постійно мінливій економічній ситуації й тривалих кризах був обраний робастний метод еліпсоїдального оцінювання стану динамічних систем при обмеженнях на перешкоди виміру виходу й швидкість їхньої зміни.

Примітка: при написанні даного автореферату магістерська робота ще не закінчена. Остаточне завершення грудень 2009р. Повний текст і матеріали по темі можуть бути отримані у автора або наукового керівника.

 Література

1. Дудко В. А. Моделювання ситуаційного керування промисловим підприємством http://www.nauka-shop.com/mod/shop/productID/15509/

2. Терлига Н. Г. Динамічна реструктуризація інвестиційного портфеля на основі методів теорії гарантованого керування http://www.nauka-shop.com/mod/shop/productID/15777/

3. Бутлова Л. В. Математичне моделювання багатокритеріальних завдань економіки з гістерезисними нелінійностями http://www.mil.ru/files/autoreferatbutova.doc

4. Зеленський В. В. Математичне моделювання інформаційних процесів в умовах економіки, що трансформується http://bankrabot.com/work/work_30390.html

5. Наукова переодика України, журнал Проблеми керування й інформатики http://www.nbuv.gov.ua/portal/natural/PUI/index.html

6. Відкритий каталог наукових конференцій, виставок і семінарів http://www.konferencii.ru/info/id/2656

7. Лебедєва И. В. Моделювання нелінійних економічних систем за допомогою динамічних рядів. // Сучасні наукомісткі технології, № 4, 2009 http://www.rae.ru/snt/?section=content&op=show_article&article_id=5312

8. Кафедра математичного моделювання систем керування - ПетрДУ http://petrsu.karelia.ru/Chairs/mmsu.html

9. Програма навчального курсу «Математичні моделі динамічних процесів в економіці». Єдине вікно доступу до освітніх ресурсів http://window.edu.ru/window_catalog/pdf2txt?p_id=12903

10. Волосов В.В. Робастні алгоритми еліпсоїдального оцінювання стану одного виду нелінійних динамічних систем. // Проблеми керування й інформатики, 2008, №1, с.36-42

11. Волосов В.В. Шевченко В.Н. Робастні методи еліпсоїдального оцінювання стану динамічних систем при обмеженнях не перешкоди виміру виходу й швидкість їхньої зміни. // Проблеми керування й інформатики, 2008, №5, с.85-93