Резюме

Гипотеза эффективных рынков утверждает, что цена актива отражает всю информацию, которая может быть получена из прошлых цен актива. Прямое заключение этой гипотезы - то, что курсы акций следуют за случайным изменением цен, и что любая прибыль, полученная из выборки во времени на рынке, зависит полностью от случайности. При отсутствии ­любой способности предсказать поведение рынка, самая лучшая стратегия — согласно сторонникам гипотезы эффективных рынков – «купить и удерживать». В этой статье мы описываем ­методологию, в соответствии с которой нейронные сети могут обучаться косвенно, используя генетический алгоритм, базирующийся на процедуре оптимизации веса, определяющим точку покупки и продажи финансовых предметов на фондовой бирже. Чтобы проверить значение отдачи, достигнутой при использовании этой методологии, мы сравниваем отдачу по четырем ценовым рядам с отдачей, достигнутой на данных случайного изменения цен при использовании процедуры самонастройки.
Эти улучшенные образцы имеют точно такое же распределение ежедневных отдачи, ровно как и оригинальный ряд, но отсутствуют какие либо зависимости в ряду, имеющиеся в оригинале. Полученные нами результаты указывают, что на некоторых ценовых рядах достигнутая отдача значительно больше чем та, которая может быть достигнуто на улучшенных образцах. Это подтверждает положение, что некоторые финансовые временные ряды не полностью случайны - противоположное гипотезе эффективных рынков положение. Поэтому торговые стратегии, базирующаяся исключительно на исторических ценовых данных, могут использоваться, чтобы достигнуть отдачи больше, чем достигнутая при использовании стратегии «купить и удерживать».
Ключевые слова:  Финансовая Торговля, Нейронные сети, Генетические ­Алгоритмы.

Введение

В подходах к прогнозу будущего поведения цен на фондовом рынке широко используются  две категории: те, которые полагаются на технический анализ, и те, которые полагаются на фундаментальный анализ. В то время как технический анализ использует только исторические данные (прошлые цены, объем торговли, изменчивость, и т.д.), чтобы определить движение цен некоторого ­финансового объекта, фундаментальный анализ основан на внешней информации (то есть, информации, которая прибывает из экономической системы, окружающей рынок). Такая информация включает процентные ставки, цены и отдачу прочих активов, и многие другие макро- или микроэкономические переменные. Использование технического анализа идет против консервативного академического мнения, которое расценивает эту гипотезу как иррациональное по сравнению с гипотезой эффективных рынков (Malkiel,1996).
Гипотеза эффективных рынков утверждает, что цена актива отражает всю информацию, которая может быть ­получена из прошлых цен актива. Аргументом является то, что любая возможность прибыли будет немедленно использована и, следовательно, исчезнет. Таким образом, рынок настолько ­эффективен, чтобы никто не может купить или продать что-то  достаточно быстро, чтобы в последствии извлечь выгоду. Следствие гипотезы эффективных рынков утверждает, что курсы акций следуют за случайным изменением цен и непредсказуемы на основании любого количества исторических данных. Таким образом, самая удачная инвестиционная стратегия – «купить и удерживать».
Несмотря на существование гипотезы эффективных рынков,­ много торговцев продолжают принимать решения покупки и продажи, основанные на исторических данных. Эти решения принимаются с предпосылкой того, что образцы существующих данных обеспечивают признак будущих движений. Если такие образцы существуют, то возможно применить автоматизированные методы распознавания образов, такие как нейронные сети, для распознавания этих образцов.
Несколько источников сообщили относительно моделирования торговых ­агентов, основанных на Искусственных Нейронных сетях.

В то время как традиционный ­подход к контролируемой оптимизации весов в нейронных сетях – известный алгоритм обратной связи (Beltratti, Margarita and Terna 1996), сообщают об использовании генетического поиска для оптимизации весов нейронной сети в этой области.

Одно из ­преимуществ генетического поиска как ­техники оптимизации веса ­ - это то, что он позволяет гибко выбирать критерии, которые могут использоваться как целевая функция, чтобы следовать в пространстве конфигураций весов. Таким образом, вместо создания решений покупки/продажи на основе числового ­предсказания цены следующего дня, генетическая на основе периода обучения.
В этой статье мы описываем методологию, в соответствии с которой ­нейронные сети могут обучаться косвенно с использованием генетического алгоритма, базирующегося на процедуре оптимизации веса, для генерации решений ­покупки и продажи финансовых объектов на фондовой бирже.
Чтобы проверить значение отдачи, достигнутой  при использовании этого метода, мы сравним отдачу по четырем финансовым временным рядам с отдачей, достигнутой по данным случайного изменения цен, полученным из каждого из этих временных рядов, используя процедуру самонастройки.
Эти улучшенные образцы имеют точно такое же распределение ежедневных отдачи, ровно как и оригинальный ряд, но отсутствуют какие либо зависимости в ряду, имеющиеся в оригинале Полученные нами результаты указывают, что на некоторых ценовых рядах достигнутая отдача значительно больше чем та, которая может быть достигнуто на улучшенных образцах. Это подтверждает положение, что некоторые финансовые временные ряды не полностью случайны - противоположное гипотезе эффективных рынков положение. Поэтому торговые стратегии, базирующаяся исключительно на исторических ценовых данных, могут использоваться, чтобы достигнуть отдачи больше, чем достигнутая при использовании стратегии «купить и удерживать».
Статья организована следующим образом:

Раздел II. Нейронные сети для автоматизации торговли

Существует один подход развитию нейронной сети торговой ­модели, согласно которому   сначала необходимо обучить нейронную сеть предсказывать стоимость цены некоторого актива в момент закрытия биржи на один или более дней вперед. Тогда решение вход/выход (покупка или продажа) может быть сделано на основе этого предсказания. Этот раздел описывает альтернативный подход, который не делает попытку точного числового предсказания номинальной стоимости, а, скорее, пытается распознать образцы во входных данных, которые могут обеспечить подсказки относительно оптимальных моментов, чтобы сделать решение покупки или продажи.
Агент от нейронной сети покупки и продажи, который мы используем, ­состоит из входящего слоя, одного скрытый слой активизирующихся сигмоидально отделений, и одинарный сигмоидально активизирующийся выход, пороговым для которого являются значение 0,5, сигналы, которые выше, интерпретируются как сигналы buy, а все другие значения ­интерпретируются как сигналы sell. Обычновход у сети – это цена актива в момент закрытия предыдущего операционного дня и переменных, полученных из этого. Они могут включать скользящие средние значений, различный прошлые входы (цена два дня назад и т.д.). На рисунке показана схематично такая сеть.

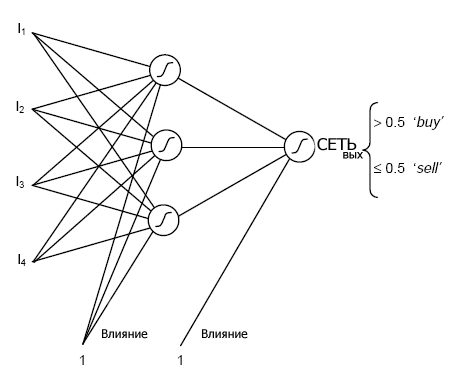
Сигналы покупки и продажи, произведенные с помощью ­сети вместе с принятой специфической торговой стратегией, определяет торговую позицию. Торговая ­стратегия, которую мы принимаем, является стратегией покупки и продажи одного пункта. Это означает, что весь ликвидный капитал ­инвестируется в акции, или весь капитал инвестируют в некоторую безопасную фиксированную процентную ставку низкого риска.

На основе торгового сигнала, сгенерированного сетью, любой вариант низкого риска уже продан и акции куплены (сигнал buy), или наоборот (сигнал sell).

Отметим, что акции могут быть только проданы, если ­инвестор в настоящее время 'на рынке', и куплены, если ­инвестор "не на рынке".
Большинство придерживается единого подхода к оптимизации веса нейронной сети - обучение обратной связью (Rumelhart & McClelland 1986). Обратная связь - контролируемый учебный ­алгоритм, который полагается на использование ряда маркированных учебных данных. Однако, прямое (то есть контролируемое) обучение сети не возможно в этом случае, так как мы не снабжены маркированными учебными данными. Таким образом, мы не знаем априорно, что является оптимальными точками покупки и продажи.
Альтернативный подход должен косвенно обнаружить ряд весов сети используя некоторый критерий, чтобы измерить эффективность торговых решений, принятых агентом, и использовать эту меру, чтобы следовать далее в пространстве конфигураций весов. Генетические алгоритмы обеспечивают выполнение каждого из этих двух пунктов.
Генетические алгоритмы (Goldberg 1989; Holland 1975) были экстенсивно применены для решения в проблемам настройки сложных параметров, в которых различные параметры системы взаимодействуют неизвестными и нелинейными путями, образуя сложную, непостоянную  поверхность отклика (Back and Schwefel и 1993 Schwefel).
Они были также применены к оптимизации весов нейронной сети (Whitley 1995). Их производительность существенно зависит от формулировки целевой функции, которая может оценить успех конкурирующих людей в решении проблемы. Так как мы желаем обнаружить торгового агента нейронной сети, который может максимизировать отдачу, мы должны сформулировать целевую функцию, ­которая определяет отдачу, сделанную агентом по данным, представляющим стоимость цены на актив в некоторый промежуток времени. Оптимальность решений агента может быть измерена в размерах финансовой отдачи, следующих за решениями агента.

_________________________________________

1 Переменные, представляющие другую информацию, могут также использоваться. Например, стоимость некоторого другого индекса или актива. В этом исследовании мы ограничиваем нас только ценами рассматриваемого актива и переменными, которые могут быть непосредственно получены из этого ряда.

Список использованной литературы:

BACK, T. and SCHWEFEL, H.P. (1993): An overview of evolutionary algorithms for parameter optimization. Evolutionary Computation, vol. 1, 1993, pp. 1-23.
BELTRATTI, A., MARGARITA, S. and TERNA, P. (1996): Neural Networks for Economic and Financial Modelling. London, Thomson Computer Press.
GOLDBERG, D.E. (1989): Genetic Algorithms in Search, Optimization and Machine Learning. Reading, Addison-Wesley.
HOLLAND, J. (1975): Adaptation in Natural and Artifi­cial Systems. Ann Arbor, University of Michigan Press.
MALKIEL, B.G. (1996): A Random Walk Down Wall Street, 6th edn. W.W. Norton, New York.
RUMELHART, D.E. and McCLELLAND, J.L. (1986): Parallel distributed processing: exploration in the mi-crostructure of cognition (Vols. 1 & 2). Cambridge, MIT Press.
WHITLEY, D. (1995): Genetic algorithms and neural networks, in Genetic Algorithms in Engineering and Computer Science. WINTER, G. and PERIAUX, J. (eds). John Wiley, PP. 203-16).