Краткосрочный численный прогноз погоды с использованием ансамблей с задержкой по времени
Авторы: Chungu Lu, Huiling Yuan, Barry E. Schwartz, and Stanley G. Benjamin.
Автор перевода: Гриценко А.В.
Источник: Weather and Forecasting, Volume 22, Issue 3 (June 2007), pp. 580–595.
1. Введение
В последние годы из-за неточностей в численном предсказании погоды (ЧПП), анализе и прогнозе, исследовательским сообществом весьма экстенсивно были изучены ансамблевые методы. Многие прогнозные центры по всему миру, такие как Европейский центр среднесрочных прогнозов погоды (ЕЦСПП) и Национальные центры экологических предсказаний (НЦЭП), так же разработали и внедрили различные ансамблевые прогнозтические системы для генерации прогнозных рекомендаций и указаний в дополнении к детерминированным. Краткосрочные ансамблевые прогнозы (КАП) представляют собой прогноз от 0 до 48 часов и используют модели ограниченного масштаба с относительно хорошими пространственными решениями и частой выдачей результата. С прогрессом вычислительной возможности и успехом среднесрочного ансамблевого прогнозирования, Брукс и другие ученые исследовали применимость КАП в ЧПП. Дю и др. (1997) исследовали воздействия начальных условий на количественное осаждение предсказывает от КАПов основанных на мезомасштабной модели. Хэмил и Колуччи (1997, 1998) вычислили выполнение модели ЕТА – Региональной спектральной модели (РСМ) КАПов Национального океанического и атмосферного управления (НОАУ). Следуя этим исследованиям, в НОАУ был разработан экспериментальнай КАП и серия сопровождающих исследований были этой системы (например Стенсруд и др. 1999; Вальдишин и др. 2001). Последующая разработка этой системы в операциях была описана учеными Дью и Тактоном (2001) и возможность включения членов из НОАУ Цикла быстрого обновления (ЦБО) прогнозной системы, это было описано Лю и др. (2004). Всесторонняя верификация КАП так же сопровождалась Хоу и др. (2001) для Штормового и мезомасштабного ансамблевого эксперимента (ШиМАЭ).
Система предсказаний НОАУ ЦБО (Бенжамин и др. 2004 а,б; Бэк и Бенджамин 1993) последовательно производили региональные прогнозы погоды в короткий период за эти годы. Поскольку система ЦБО ассимилирует высокочастотные данные в почасовом цикле, его 12-ти часовые прогнозы обеспечили ценные данные и дополнение к менее часто обновляемым прогнозам от других эксплуатационных моделей НОАУ. По той же самой причине, удивительно как прогнозы из этих почасовых инициализаций изменяются, и, если есть некоторая изменчивость, насколько выполнимый и разумный ансамблевый прогноз при использовании этих прогнозов как ряд ансамблевых участников.
Ансаблевое прогнозирование с задержкой по времени было изучено и предложено для среднего диапазона из 6-10 дней (Хофманн и Калнай 1983; Далчер и др. 1988; Ван ден Дул и Раховец 1994). Это понятие было также недавно применено к прогнозу короткого диапазона в работе Хоу и др. (2001) и у Валсер и др. (2004). Мы экспериментировали с ансамблевым подходом с задержкой времени, используя НОАУ ЦБО в течение многих лет. Мы полагаем, что методика, которую мы представляем в этом исследовании, может быть применена к любой быстрой ассимиляции обновления данных и системе прогноза.
Одна причина принять ансамблевую технику с задержкой времени к прогнозу короткого диапазона состоит в том, что кратковременные предсказания, обладают относительно сильной зависимостью от начальных условий. Ошибки прогноза в очень коротком диапазоне могут быть сильно коррелированы к неуверенности в начальном анализе. Ограниченные по времени ансамбли могут интерпретироваться как прогнозы, полученные из ряда начальных условий (Ван ден Дул и Раховец 1994). Поскольку эти начальные расчеты произведены от различных циклов инициализации прогноза, концептуально, изолированные временем ансамбли отражают ошибочную ковариацию прогноза с развитием времени. В очень коротком диапазоне эта потокозависимая ошибка прогноза может быть, например, результатом начальной неустойчивости или шоком модельных областей из-за различных данных, поглотивших во время инициализации и следующее регулирование модельных областей.
В этом исследовании мы сообщим, как ансамблевая система предсказаний может быть построена, используя прогнозы из ЦБО, и оценить, сколько навыка этот тип ансамблевого прогноза может обеспечить по каждому отдельному детерминированному прогнозу на очень короткое погодное предсказание диапазоном от 1 до 3 часов. Этот тип краткосрочной ансамблевой системы предсказаний может использоваться в краткосрочных системах поддержки принятия решений, таких которые используются для прогноза погоды в авиации, включая управление воздушным движением, когда необходимы частые обновления прогноза. Будут проводиться исследования и проверка этих ансамблевых систем с задержкой времени и систем вероятностного прогноза. Мы введем два разных подхода для ЦБО, ежечасное предсказание и сравнение усовершенствование прогнозов короткого диапазона этими двумя ансамблевыми системами.
Статья организована следующим образом. В разделе 2 мы сначала дадим краткое описание ассимиляции данных НОАУ ЦБО и моделирования системы. Мы исследуем изменчивость прогноза среди прогнозов от различных циклов инициализации. Затем, мы опишем, как построить временные ансамбли с задержкой времени, используя восемь доступных детерминированных прогнозов в пределах 12-ти часового цикла инициализации, и кратко проведем проверку данных наблюдения и метода. В следующем разделе мы получим ансамблевые прогнозы с задержкой времени, используя простой ансамблевый средний подход. Эти ансамбли с задержкой времени наряду с различными детерминированными прогнозами проверены против верхнего воздуханаблюдения в станционных местоположениях (раздел 3). Чтобы далее уменьшить ошибку ансамблевого прогноза, мы строим кратковременные ансамбли с неравно полученными прогнозами, используя мультилинейный метод регресса (раздел 4). Заключения будут приведены в разделе 5.
2. Ансамблевый метод с задержкой по времени
a. Описание прогностической модели
Система прогнозирования НОАУ ЦБО была разработана в лаборатории систем прогнозирования НОАУ (в настоящее время, НОАУ/Лаборатория исследования Земли/Глобальная система деления) и была использована как оперативная модель прогноза для Федерального управления авиации (ФУА) и в качестве быстро обновляемого прогноза и системы ассимиляции данных в НОАУ/НЦЭП. Динамическое ядро модели составлено из гибридной ландшафтно-зависимой сигмы (на низких уровнях) и изэнтропийных (на высоких уровнях) вертикальных координат, и ряда гидростатических примитивных уравнений. Кроме того, есть полный комплект физических схем параметризации, включая те, которые предназначены для планетарного граничного слоя, радиации, физики поверхности земли, конвекции кучевых облаков, и явной физики облаков смешанной фазы, для представления в модели различных физических процессов и завершения модельных динамических уравнений. Система ассимиляции данных включает серию реализаций оптимальной интерполяции (ОИ), трехмерного вариационного анализа данных ассимиляции (3DVAR) и несложных технических приемов. Несложные технические приемы главным образом применимы к поверхностным пространствам, пока основные атмосферные пространства обрабатываются с помощью алгоритма 3DVAR. Поперечные граничные условия предоставляются моделью Eta НЦЭП.
Горизонтальная размерность ЦБО покрывает прилегающие Соединенные Штаты и смежные области Канады и Мексики, а также Тихий и Атлантический океаны. Экспериментальный ЦБО был запущен по ряду горизонтальной сетки расстояний: 60, 40, 20 и 13 км. В этом исследовании мы использовали анализы и прогнозы 40-км размерности в течение ноября и декабря 2003 года. Выполняется 24 запуска в день, но мы используем только прогнозы, которые инициализируются с использованием предыдущих 12 часов. Ежечасный запуск экспериментального ЦБО данных 40 км архивируются только для первых 6 часов с более длинными архивами, ограниченными 3-часовыми пробегами (например, 0000, 0300, 0600 UTC, и т.д.).
b. Неустойчивость ежечасных прогнозов ЦБО
Для исследования неустойчивости ежечасных прогнозов ЦБО, мы случайным образом подобрали случай из архива оперативных прогнозов ЦБО в течении зимы 2003/2004 годов. Случай составляет прогнозы, действительные для 0000 UTC 15 декабря 2003, и инициализируется, соответственно, в предыдущие 12, 9, 6, 3, 2, и 1 часов. В этом случае были использованы две зимние синоптические системы погоды, наиболее очевидные в этих прогнозах: система отсечения низкого давления вдоль восточного побережья Соединенных Штатов, расположенного по штатам Новой Англии, и глубокого низкого давления через вытягивание от центральной Канады до центральной части Соединенных Штатов, с сильной адвекцией холодного воздуха арктических воздушных масс из западной Канады в западную часть Соединенных Штатов.
В то время как прогнозы представляют последовательно большие картинки геопотенциальных высот пространства, выявляются некоторые несогласованности на глубине (интенсивности) двух синоптических систем. В частности, чем «старше» прогноз, тем больше различие в прогнозе на 1 час.
c. Структура ансаблевой системы с задержкой по времени
Поскольку мы заинтересованы в краткосрочном ансамблевом прогнозировании, только детерминированные прогнозы в пределах 12-часового цикла (предыдущие прогнозы до 12 часов) рассматривают объединения частей ансамбля. Рисунок 3 показывает схематично ансамблевую систему прогноза с задержкой по времени. В связи с тем, что данные прогноза ежечасной инициализации для 40-км ЦБО были заархивированы до 6 часов, после этого данные прогноза только трехчасовой инициализации были заархивированы, максимальный размер ансамбля с временной задержкой с которой мы могли работать в 12 часовом цикле – 8 частей (см. рис. 1). Ансамбль с временной задержкой – одиночная модель, ансамблевая система прогнозирования с начальными условиями; т.е. модель динамики, физической параметризации и чисел. Различия среди частей ансамбля основаны на различных проекциях прогноза или прогнозной инициализации в различное время.
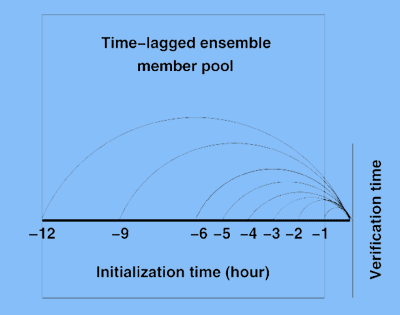
Рисунок 1 - Схематическая диаграмма устройства системы ансамблевого прогноза со сдвигом по времени
В данном исследовании, мы концентрируемся на выполнении ансамблей с временной задержкой для очень краткосрочных прогнозов на 1-3 часа. Когда число валидации установлено, между 0000 и 1200 UTC, число ансамблей увеличивается на 1 составляющую. Поэтому, максимальные числа ансамблей – 8, 7 и 6 для прогноза на 1, 2 и 3 часа, соответственно, учитывая конфигурацию архива ЦБО. На рис. 2 представлены результаты подведения итогов доступных детерминированных прогнозов, которые используются для составления ансамбля с временной задержкой для проверочного прогноза на 1-, 2- и 3 часа задержки.
d. Проверка-наблюдение данных и метода
Проверка прогнозов (и детерминированного и ансамблевого) была выполнена способом интерполяции сетки прогнозного пространства ЦБО данных наблюдательных постов, далее сравнения прогнозных значений переменных состояния (высота, температура, относительная влажность и скорость ветра) с наблюдаемыми, с обязательным согласованием уровней давления (850, 700, 500, 400, 250, 200, и 150 гПа). Ошибки прогноза (прогноз – наблюдение) были рассчитаны с условием, что наблюдения представляют правду.
Мы использовали наблюдения оперативного радиозонда (дважды в день), около 92 станций в области модели ЦБО.
3. Одинаково взвешенные ансамбли
a. Ансамблевый средний прогноз
Самый простой способ получить ансамблевый прогноз состоит в том, чтобы взять среднее арифметическое значений участников ансамблевого:
 (3.1)
(3.1)
где f^ и fi, i=1,2,...,N, обозначают ансамблевый прогноз, и детерминированные прогнозы N, соответственно, и (x, t) обозначают пространственный и времянезависимые переменные. Число ансамбля предсказывало, что участники изменяются между 6 и 8, в зависимости от проверки специфической задержки прогноза (см. рис. 2). Очевидно, этот ансамблевый прогноз получен просто, нагружая всех участников прогноза одинаково.
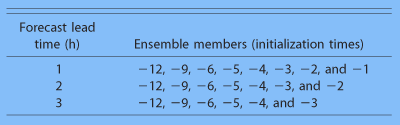
Рисунок 2 - Ансамблевые системы с временным сдвигом для разных прогнозов
b. Краткосрочное прогнозное усовершенствование
Чтобы исследовать, сколько усовершенствований ансамблевые прогнозы с задержкой по времени могут обеспечить, мы сначала вычисляем множество навыков средней абсолютной ошибки, используя каждый детерминированный прогноз как справочный прогноз:
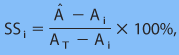 (3.2)
(3.2)
где A^=<|f^-fT|> является мерой точности ансамблевого прогноза, Ai=<|f^-fT|> мера по точности справочного детерминированного прогноза, AT=0 (здесь для случая наблюдательных ошибок), и fT - проверка типа "истина". Угольники представляют пространственное и временное среднее число.
На рис. 3a–d, изображено множество навыка прогноза геопотенциальной высоты, температуры, скорость ветра (определенный величиной горизонтальных векторов ветра), и относительная влажность в 850-, 500-, и 250-hPa уровнях давления для временных ансамблей с задержкой по времени с детерминированными прогнозами 1–3 часов как справочные прогнозы. Наблюдаем ситуацию, что у ансамблевых прогнозов есть положительный навык по соответствующим детерминированным прогнозам. Усовершенствование прогнозов колеблется от нескольких процентов до 10 %, в зависимости от переменных прогноза и уровней. Можно заметить: от этих чисел, усовершенствование прогноза вообще меньше на верхних уровнях и для областей ветра. Усовершенствования для 1-, 2-, и прогнозы 3-часовых вообще сопоставимы. Для области высоты есть немного больше усовершенствования 1-часовых прогнозов 2-часовых чем в прогнозе 3-часовом; в то время как для температуры и скорости ветра, немного больше усовершенствования найдено в 2-часовых прогнозах и 3-часовых чем в прогнозе 1-часовом. Для относительной влажности относительно существенное усовершенствование найдено на уровне давления в 500-hPa.
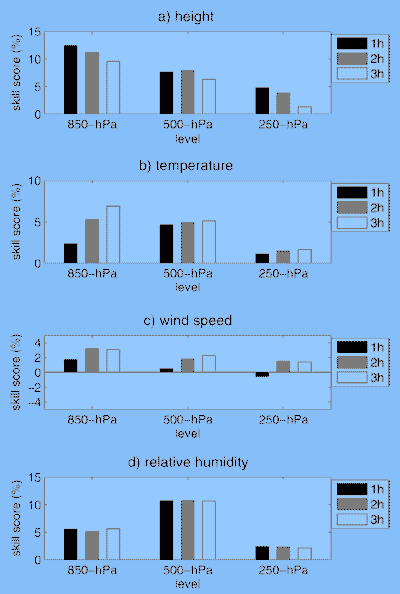
Рисунок 3 - Прогнозные уровни умения, внедренные ансамблем с временной задержкой с 1–3-часовыми ЦБО детерминированными прогнозами, оцененными с наблюдениями радиозонда ("правда") в трех разных уровнях: 850, 500, and 250 hPa. Темный, средний и светлый столбик для прогнозов с задержкой времени 1, 2, и 3 часа, соответственно. Показаны как (a) геопотенциальная высота, (b) температура, (c) горизонтальный ветер, и (d) относительная владность
Множество навыка отражает усредненное усовершенствование прогноза по всей области, покрытой участками радиоветровым зондом. Можно также знать в том, сколько участков это усовершенствование прогноза фактически покрыло. Чтобы ответить на этот вопрос, мы оцениваем ошибку прогноза на каждой станции и считаем число станций, на которых у ансамблевого прогноза меньше ошибки, чем делает детерминированный прогноз. На Рис. 4a и 4b процент от проверки по времени, в которые ансамблевый прогноз лучше чем детерминированный прогноз как вертикальные профили для 1-, 2-, и 3-часовой ветер и температурные прогнозы, соответственно. Мы видим, что процент от времен проверки, в течение которых ансамблевый прогноз выступает лучше чем детерминированный прогноз, очень высок, и что эти уменьшения процента в более высоких уровнях (достигает минимума на 300-hPa уровне давления для ветра и 200-hPa уровне для температуры). Это уменьшение в усовершенствовании процента в более высоких высотах совместимо с вычислением показателя навыка, показанным на рис. 3. Одно из объяснений уменьшения навыка на этих уровнях - маленький эффект сглаживания, обеспеченный средствами ансамбля, он разбит большой скоростью ветра и большим изменением температуры на реактивных уровнях (200–300 hPa).

Рисунок 4 - Вертикальные профили процента от общего числа проверки ансамбля означают, что прогноз был лучше, чем детерминированный прогноз ЦБО для периода ноябрь-декабрь 2003 года для (a) прогнозов горизонтального ветра и (b) прогноза температуры
c. Распространение ансамбля
Чтобы исследовать распространение ансамблевой системы с задержкой по времени, покажем гистограмму разряда (диаграмма Талагранда) для отобранных образцовых областей от каждой категории проверки (1-3-часовые прогнозы). Гистограммы для 1-, 2-, и 3-часовых прогнозов задержки показаны на рис. 5a1–a3 для геопотенциальной области высоты на 500-hPa уровне давления, Рис. 5b1–b3 для температурной области на 850-hPa уровне давления, Рис. 5c1–c3 для области ветра на 250-hPa уровне давления, и Рис. 5d1–d3 для относительной влажности в 850-hPa. Это указывает, что ансамбли с задержкой по времени составляют наддисперсионную систему ансамблевую систему прогноза (Хэмиль 2001). Есть несколько факторов, которые способствуют небольшой проблеме распространения в ансамблевой системе с задержкой по времени. Во-первых, ансамбль с задержкой по времени прогнозировал, что система - одно-образцовая ансамблевая система: это плохо сказывается на образцовой ошибке, которая имеет тенденцию давать наибольшое распространение ансамбля. Во-вторых, ансамблевая система построена непосредственно из прогнозов с различными проектированиями прогноза. Поэтому, нет никакого цикла размножения (как в методе НЦЭП) и никакая процедура максимизации (как метод исключительного вектора, используемый в ЕЦСПП) для роста "волнений". В-третьих, потому что все инициализации так друг близко к другу, что образцовая динамика будет иметь все значения среди участников ансамбля, растущих минимально (близко к линейной моде). Наконец, маленький размер ансамбля уменьшает его способность внести полную неуверенность в прогнозе. Также обозначено по этим гистограмм: небольшие уклоны обнаружены во всех областях на различных уровнях (из-за клонившихся распределений гистограмм разряда к одной стороне). Эти уклоны происходят вероятно из-за уклонов в образцовом фоне, которые ассимилируют данные, и затем представляются в цикле анализа.
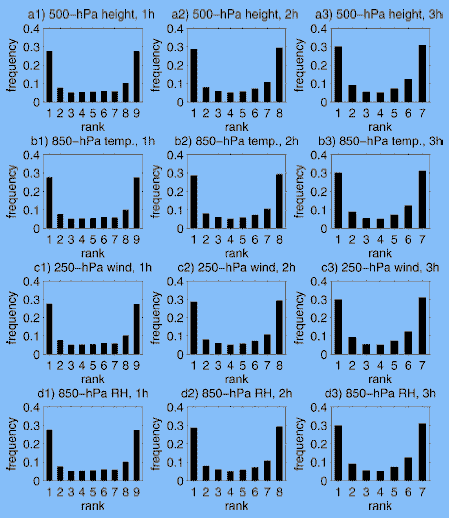
Рисунок 5 - Гистограмма ранга для детерминированных прогнозов ЦБО с временной задержкой для (a) 500-hPa геопотенциальной высоты, (b) 850-hPa температуры, (c) 250-hPa скорости ветра, и (d) 850-hPa относительной влажности, проверенные для прогнозов с задержкой времени 1, 2, и 3 часа
d. Анализ усовершенствования прогноза ансамблями с задержкой по времени
Чтобы понять, почему ансамблевая система с задержкой по времени улучшает прогнозы короткого диапазона, мы готовим ошибку прогноза как функцию времени инициализации (Рис. 6a–d) для следующих переменных прогноза на трех различных уровнях давления: геопотенциальная высота, температура, скорость ветра, и относительная влажность. Ошибки прогноза КАП, детерминированные прогнозы, калибровавшие в 12, 9, 6, 5, 4, 3, 2, и 1 час, показаны как сплошные жирные кривые, те что со звездочками отмечают свои ошибочные размеры. Различные типы линий представляют ошибки прогноза для ансамблевых систем с задержкой по времени с тремя различным временными отрезками для прогноза (см. рис. 2). Поскольку есть только одна ценность для каждой ошибки ансамблевого прогноза, или оцененной как 1-, 2-, или 3-часовых прогнозов, должен быть только один пункт, представленный по той ошибке в этой графе. Однако, мы используем горизонтальные линии, чтобы указать эти ошибки, данные этими ансамбливыми системами. Отмечаем, что длины этих линий изменяются, указывая на различные размеры ансамблей по восемь, семь, и шесть участников, соответственно, для 1-, 2-, и 3-часовых прогнозов.
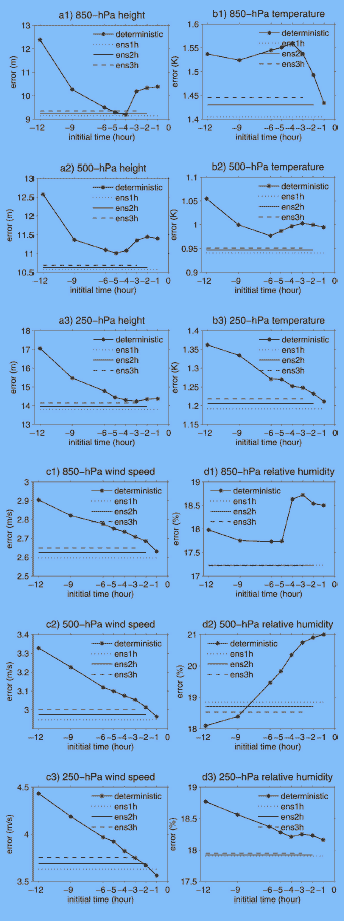
Рисунок 6 - Ошибки прогноза (a) геопотенциальной высоты, (b) температуры, (c) горизонтальной скорости ветра, и (d) относительной влажности как функции модели инициализации времени. Сплошная кривая с нанесенными точками для детерминированнх прогнозов с различных проекций прогнозов. Три различных типа горизонтальных линий на каждую группу, соответствующим прогнозам на 1-, 2-, и 3-часа, со значениями ошибок, которые указывают какая составляющая детерминированного прогноза включена
Объяснив, как рис. 6a–d был создан, давайте исследуем то, что эти фигуры нам показывают. Рисунок 6c показывает ошибки прогноза в области ветра. Ошибочная кривая для детерминированных прогнозов непрерывно снижается, поскольку время инициализации становится ближе и более близким ко времени проверки. Эта ситуация, кажется, соответствует традиционному размышлению, что инициализация с более свежими данными произведет более точный прогноз. В этом случае, усовершенствование прогнозов, сделанных ансамблями, кажется, минимально (или абсолютно ни один, например, на 250-hPa уровне для 1-часового прогноза), который совместим с рис. 3c (только несколько процентов навыка или даже отрицательного навыка). Это минимальное усовершенствование прогноза может произойти из-за среднего числа ансамбля, которое немного уменьшает образцовые случайные ошибки. Исследуя рис. 6a, 6b, и 6d, можно увидеть, что эта картина не всегда верна. Ошибка прогноза, связанная с детерминированным прогнозом, калибровавшим все дальше назад, таким как 12-часовой или 9-часовой прогнозы, типично показывает большую ошибку. Эта ошибка уменьшается, поскольку инициализация придвигается поближе ко времени проверки. Однако, когда инициализация добирается до очень короткого диапазона 1–3-часов, ошибка прогноза может увеличиться снова для определенных переменных прогноза на определенных уровнях. Это явление обычно понимается как проблема "образцовая начальная раскрутки" (спинап). Есть два типа этой проблемной модели. Один тип следует из образцовой внутренней связанной с физической передачей тепла. Этот тип проблемной модели обычно отражается в образцовой конвекции и областях осаждения. Другой тип данной проблемной модели возникает потому, что существует определенный период времени для массы и областей ветра, чтобы приспособиться друг к другу.
В зависимости от типа данных и масштаба погодных особенности, спинап проблема может произойти на отобранных образцовых переменных. Когда они случаются, например, в случаях геопотенциальной высоты и областей относительной влажности на всех уровнях в рис. 6a и 6d, и в случае температуры в 850-и 500-hPa уровнях в рис. 6b1 и 6b2, существенное усовершенствование ансамблевым прогнозом более вероятно. Рисунки 3a и 3d также подтверждают эту картину, где 10 % или большие навыки прогноза могут быть достигнуты ансамблевой системой с задержкой по времени. Ошибка анализируется для геопотенциальной высоты, температуры, скорости ветра, и относительной влажности на рис. 6a–d совместимы с нашими предыдущими результатами (Бенжамин и др. 2004b, их рис. 7a–c). Конечно, усовершенствование прогноза происходит также из-за эффекта сглаживания среднего ансамбля, который имеет тенденцию уменьшать интенсивные образцовые особенности.

Рисунок 7 - Значения компонента ПТ и весовых коэффициентов (для различных детерминированных прогнозов) обученных с наблюдениями радиозонда за период ноября 2003 года с использованием мультилинейного регрессионного алгоритма
4. Неравноценно взвешенные ансамбли
a. Мультилинейный регрессионный метод
Из анализа в разделе 3, мы знаем, что ансамблевые системы с задержкой по времени совершенствуют краткосрочные прогнозы, причина в том, что среднее детерминированных прогнозов, инициализированных в разное время, сглаживает начальные неточности модели и что ансамбль означает, как правило, хорошую проверку, из-за сглаживания серьезных модельных особенностей. Тем не менее, приближение равноценно взвешенного ансамбля представляет, очевидно, недоработанный способ получения ансамбля прогнозов. Мы могли бы еще больше уменьшить ошибки прогноза, выбирая различные веса для различных составляющих прогнозов в зависимости от их уровня дисбаланса. При этом мы используем полилинейный регрессионный метод, сходный с методом, предложенным Ван ден Дулом и Раховцем (1994).
Позвольте нам выразить ансамблевый прогноз как взвешенную комбинацию детерминированных прогнозов; т.е.
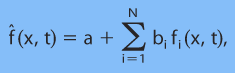 (4.1)
(4.1)
где bi – N весовых коэффициентов для N составляющих прогноза, а – ПТ (постоянный ток). Требуя, чтобы ошибка наименьших квадратов была заключена между прогнозами ансамбля и проверочной правдой, можно получить ряд линейных уравнений для набора регрессионных коэффициентов:
 (4.2)
(4.2)
где
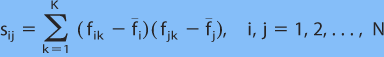 (4.3)
(4.3)
и
 (4.4)
(4.4)
ковариация между самими детерминированными прогнозами, и ковариация между проверочной правдой и детерминированными прогнозами, соответственно. В (4.3) и (4.4), вычисление ковариации взято по всем значениям проверки k=1,2,...,K, и fi и fT ожидаемые значения детерминированных прогнозов и проверочной правды, соответственно. Мы использовали данные одного месяца для периода обучения, и данные другого месяца для проверки, и мы также провели взаимную ратификацию, меняя местами периоды обучения и проверки. Ожидаемые значения в вышеуказанных уравнениях были получены из среднего числа всего периода обучения.
После решения (4.2), каждый получает ряд коэффициентов регрессии (веса) для каждого детерминированного прогноза, используемого для участника ансамбля. Компонент ПТ может быть определен однажды bi, i=1,2,...,N, как известно:
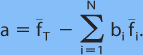 (4.5)
(4.5)
Ансамблевая система прогноза может быть построена как (4.1) из этих оптимально стойких весов.
Мы развили версию ансамблевой системы прогноза ЦБО с задержкой по времени, основанной на этом мультилинейном регрессионном методе. Поскольку детерминированные прогнозы инициализируются в предшествующие моменты и наблюдения соответствующие этим временам все существуют до времени прогноза, этот алгоритм может быть представлен как ансамблевая система прогноза в реальном времени.
b. Обучаемые веса
На рисунках 7a–d показаны весовые коэффициенты как функции детерминированных прогнозов для высоты, температуры, скорости ветра, и относительной влажности, соответственно, на уровнях давления в 850-, 500-, и 250- гПa. Для существующего случая данные радиоветрового зонда за ноябрь 2003 года используются для обучения детерминированных прогнозов ЦБО. Поправки для компонента ПТ для этих переменных на различных уровнях обозначены в легенде. Вообще, мультилинейная регрессионная схема пытается минимизировать различие между предсказателем и прогнозируемой величиной, достигая баланса среди компонента ПТ и всех других изменяемых компонентов (весов). В то время как компонент ПТ обеспечивает исправление отклонений (независимое различие), весовые коэффициенты отражают относительную важность каждого содействующего участника прогноза. Абсолютная величина для каждого коэффициента на рис. 9a–d дает представление о размере веса конкретного прогноза, в то время как положительный или отрицательный признак весового коэффициента для специфического прогноза представляет вес или противовес для полной минимизации.
Можно видеть из рис. 7c, в дополнении к рис. 6c, что, когда ошибка прогноза уменьшения ветра однородна от старых до более новых прогнозов, обучаемые весовые коэффициенты, соответствующие этим прогнозам, не обладают линейным снижением размера веса. Вместо этого учебный процесс попытался поместить почти весь вес к самому точному прогнозу, и назначил тривиальные веса на все другие прогнозы, но с чередованием веса и противовеса (изменения вокруг нулевой линии). Ясно, что линейный регрессионный алгоритм пытается иметь дело не только с моделями раскрутки ошибки, но также и с другими случайными моделями ошибки.
Когда начальные модельные ошибки являются очевидными, например, в высоте и областях относительной влажности (рис. 6a и 6d), образцы весов очевидно различны (рис. 7a и 7d), в том смысле, что прогноз на 1 час более не обладает доминирующим весом, но веса подобной величины могут также быть найдены с 2-, 3-, 4-, 5-, и даже 12-часовых прогнозов. Температура на различных уровнях на Рис. 6b - случай объединения двух сценариев, обсужденных выше. Поэтому, его образец веса (рис. 9b) показывает смешение особенностей между двумя противоположными случаями.
Полный обученный образец для весовых коэффициентов очень подходит для использования данных декабря 2003, которые показательны из некоторого уровня надежности в учебных результатах.
c. Проверка неравноценно взвешенных ансамблевых прогнозов
Взаимная ратификация использовалась для управления процессом неравных весов на ноябрь и декабрь переключением месяцев обучения и проверки. Мы сначала сравниваем прогнозы, сделанные одинаково взвешенными и неравноценно взвешенными системами ансамбля в течение периода ноября-декабря 2003. Чтобы сделать это, мы вычисляем уровни умения для неравноценно взвешенных прогнозов ансамбля, используя одинаково взвешенные ансамбли как справочные прогнозы. Таким образом, мы можем точно идентифицировать относительные возможности этих двух методов. Иллюстрации 8a–d показывают уровни умения для четырех прогнозируемых переменных прогноза на трех различных уровнях давления. Можно видеть, что неравноценно взвешенные ансамбли обеспечили намного лучшие 1-3 часовые прогнозы, чем это делают одинаково взвешенные ансамбли. Для всех переменных и на всех уровнях, неравноценно взвешенный ансамбль прогноза показал положительные навыки.
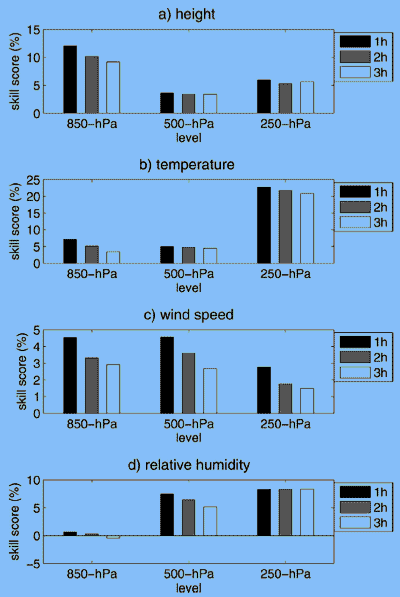
Рисунок 8 - Уровни умения прогноза для (a) геопотенциальной высоты, (b) температуры, (c) ветра, и (d) относительной влажности для неравноценно взвешенных ансамблевых систем на 850-, 500-, and 250-hPa уровнях давления. Уровни вычислены с использованием одинаково взвешенных ансамблей как образцового прогноза для прогноза с задержкой по времени 1, 2, и 3 часа
Чтобы представить этот результат на большей картинке, мы теперь представим 1-3 часовые ошибки прогноза для детерминированного и для двух ансамблевых прогнозов. На рис. 9a–d, мы изобразили прогнозы от одинаково и неравноценно взвешенных систем ансамбля, чтобы сравнить детерминированным прогнозом ЦБО. По этим рисункам можно отметить, что хотя одинаково взвешенные ансамбли улучшают краткосрочные прогнозы в большинстве случаев по сравнению с детерминированными прогнозами, ансамбли, использующие неравные веса, делают существенное усовершенствование по детерминированным прогнозам для всех переменных на всех уровнях. Мы должны также указать, что снижения ошибки, показанные на рис. 9, кажется, являются маленькими в абсолютном смысле, по причине этих значений для области и среднего времени.
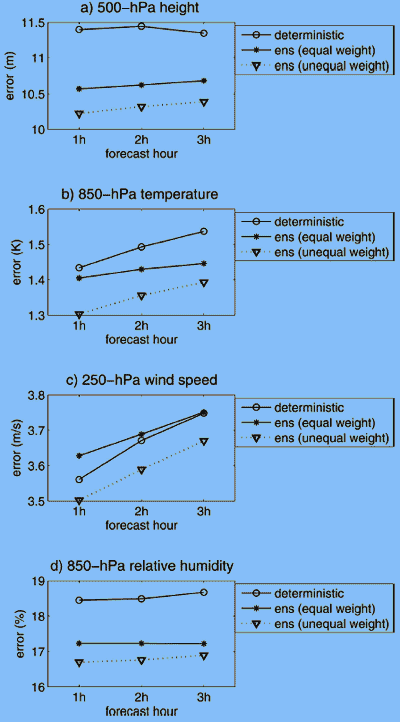
Рисунок 9 - Сравнение ошибок прогноза для одинаково взвешенных ансамблей, неравноценно взвешенных ансамблей, и детерминированных прогнозов для (a) 500-hPa геопотенциальной высоты, (b) 850- hPa температуры, (c) 250-hPa ветра, и (d) 850-hPa относительной влажности как функции прогнозного времени
5. Заключения
В этом исследовании мы продемонстрировали, как построить ансамблевую систему с задержкой по времени, используя детерминированные прогнозы от быстрой системы ассимиляции данных обновления прогноза, такие как НОАУ КАП. Использовались методы одинаково нагруженные и неравноценно нагруженные, чтобы объединить эти прогнозы. Проводились исследования и проверки средних по ансамблевым и вероятностным прогнозам. Результаты могут быть получены следующим образом.
1) У одинаково взвешенных средних ансамблевых прогнозов есть некоторый положительный навык прогноза по детерминированным прогнозам на короткий диапазон 1–3 часа.
2) Ансамблевая система, составленная из КАП и детерминированных прогнозов, является наддисперсионной.
3) Из анализа коэффициентов надбавки усовершенствование ансамблевых прогнозов с задержкой по времени следует то, что ансамбль с задержкой по времени исправляет ошибки прогноза, следующие из модели спинап.
4) Неравноценно взвешенные ансамбли обеспечивают лучшие ансамбливые системы. Эти ансамблевые системы приводят к существенному усовершенствованию детерминированных прогнозов в коротком диапазоне 1–3 часов.
Источники
Benjamin, S. G., G. A. Grell, J. M. Brown, and T. G. Smirnova, 2004a: Mesoscale weather prediction with the RUC hybrid isentropic–terrain-following coordinate model. Mon. Wea. Rev., 132, 473–494.
——, and Coauthors, 2004b: An hourly assimilation–forecast cycle: The RUC. Mon. Wea. Rev., 132, 495–518.
Bleck, R., and S. G. Benjamin, 1993: Regional weather prediction with a model combining terrain-following and isentropic coordinates. Part I: Model description. Mon. Wea. Rev., 121, 1770–1785.
Brooks, H. E., M. S. Tracton, D. J. Stensrud, G. DiMego, and Z. Toth, 1995: Short-range ensemble forecasting: Report from a workshop, 25–27 July 1994. Bull. Amer. Meteor. Soc., 76, 1617–1624.
Dalcher, A., E. Kalnay, and R. N. Hoffman, 1988: Medium range lagged forecasts. Mon. Wea. Rev., 116, 402–416.
Du, J., and M. S. Tracton, 2001: Implementation of a real-time short-range ensemble forecasting system at NCEP: An update. Preprints, Ninth Conf. on Mesoscale Processes, Fort Lauderdale, FL, Amer. Meteor. Soc., 355–356.
——, S. L. Mullen, and F. Sanders, 1997: Short-range ensemble forecasting of quantitative precipitation. Mon. Wea. Rev., 125, 2427–2459.
Hamill, T. M., 2001: Interpretation of rank histograms for verifying ensemble forecasts. Mon. Wea. Rev., 129, 550–560.
——, and S. J. Colucci, 1997: Verification of Eta–RSM shortrange ensemble forecasts. Mon. Wea. Rev., 125, 1312–1327.
——, and ——, 1998: Evaluation of Eta–RSM ensemble probabilistic precipitation forecasts. Mon. Wea. Rev., 126, 711–724.
——, and J. Juras, 2007: Measuring forecast skill: Is it real skill or is it the varying climatology? Quart. J. Roy. Meteor. Soc., in press.
Hoffman, R. N., and E. Kalnay, 1983: Lagged average forecasting, an alternative to Monte Carlo forecasting. Tellus, 35A, 100– 118.
Hou, D., E. Kalnay, and K. K. Droegemeier, 2001: Objective verification of the SAMEX’ 98 ensemble forecasts. Mon. Wea. Rev., 129, 73–91.
Jolliffe, I. T., and D. B. Stephenson, 2003: Forecast Verification: A Practitioner’s Guide in Atmospheric Science. John Wiley and Sons, 240 pp.
Lu, C., S. G. Benjamin, J. Du, and S. Tracton, 2004: RUC Short-Range Ensemble Forecast System. Preprints, 20th Conf. on Weather Analysis and Forecasting, Seattle, WA, Amer. Meteor. Soc., CD-ROM, J11.6.
Stanski, H. R., L. J. Wilson, and W. R. Burrows, 1989: Survey of common verification methods in meteorology. WMO World Weather Watch Tech. Rep. 8, 114 pp.
Stensrud, D. J., H. E. Brooks, J. Du, M. S. Tracton, and E. Rogers, 1999: Using ensembles for short-range forecasting. Mon. Wea. Rev., 127, 433–446.
van den Dool, H. M., and L. Rukhovets, 1994: On the weights for an ensemble-averaged 6–10-day forecast. Wea. Forecasting, 9, 457–465.
Walser, A., D. Luthi, and C. Schar, 2004: Predictability of precipitation in a cloud-resolving model. Mon. Wea. Rev., 132, 560–577.
Wandishin, M. S., S. L. Mullen, D. J. Stensrud, and H. E. Brooks, 2001: Evaluation of a short-range multimodel ensemble system. Mon. Wea. Rev., 129, 729–747.
Wilks, D. S., 1995: Statistical Methods in the Atmospheric Sciences:An Introduction. Academic Press, 467 pp.
Wilson, L. J., 2000: Comments on “Probabilistic predictions of precipitation using the ECMWF Ensemble Prediction System.” Wea. Forecasting, 15, 361–364.