Логические операции составляют основу многих программ, имеющих элементы искусственного интеллекта (ИИ). Это касается не только экспертных систем, но и систем распознавания, машинного перевода с одного языка на другой, логических игр и др.
Формальная (бинарная) логика, известная со времен Аристотеля, реализована практически во всех языках программирования. В Delphi это тип Boolean и производные от него, операции AND, OR, NOT ... . Для систем ИИ данный подход не всегда приемлем, так как он не допускает возможности оперировать промежуточными значениями между ДА и НЕТ.
Для решения этой проблемы можно предложить различные методы.
Во-первых - применить законы теории вероятностей. Вместо логической величины используется вероятность (дробное число от 0 до 1).
Однако, попытки применения вероятностных законов не всегда приемлемы в системах ИИ. Например, эксперные оценки не удовлетворяют требованиям, предъявляемым к вероятности. Если определить вероятность, как отношение числа благоприятных исходов к общему числу всех РАВНОВОЗМОЖНЫХ НЕСОВМЕСТНЫХ исходов, то ясно, что экспертные оценки не удовлетворяют данным требованиям и применение вероятностных законов иногда приводит к курьезным результатам.
Например, эксперт определил, что надежность станка в течение смены P = 0.8 . Какова вероятность того, что из 10 таких станков хотя-бы один выйдет из строя. Получаем Вероятность поломки одного N = 1 - 0.8 = 0.2 Вероятность поломки одного из 10 по закону сложения вероятностей R = 0.2 * 10 = 2. Вероятность не может превышать 1, значит экспертная оценка неверна или вероятностная методика просто не подходит в данном случае.
Второй подход состоит в применении правил нечеткой логики. Известны различные реализации логических правил. Чаще всего для операции ИЛИ используют функцию максимума, для операции И - минимума.
Эту реализацию можно (и нужно) подвергать критике, но, как ни странно, она работает в ряде экспертных систем и дает вполне нормальные результаты.
Вашему вниманию предлагается модуль RealLogic, написанный в Delphi 2.0 (должен работать и в других), который реализует данный подход.
Значения экспертных оценок представлены числами в диапазоне от 0 до 1. Это удобно для вычислений и сохраняется аналогия с вероятностью. Значение 0 означает отсутствие данного факта (или уверенность в его отсутствии, ведь метод весьма приближенный), 1 - уверенность в том, что факт имеет место быть. Значение 1/2 - состояние неопределенности, когда не ясно присутствует или отсутствует данный факт. В ряде случаев есть потребность разделить неопределенное и неизвестное состояние. Я предлагаю для неизвестных фактов присваивать значение -1 (минус один). Оно не укладывается в систему, но ничего не поделаешь.
В литературе приводятся и другие системы измерений оценок, например пятибалльная система удобна тем, что нет надобности оперировать с вещественными числами. Целые числа обрабатываются быстрей и занимают меньше памяти. Встречались системы -1(нет) ... 0(неопределенно) ... 1 (да) и другие.
Текст модуля приведен в конце статьи.
Для проверки работы модуля написаны тестовые примеры.
Первый пример иллюстрирует работу логических операций. Полосы прокрутки задают значения веса исходных фактов А, B. По нажатию одной из кнопок вычисляется результирующий факт C.
Вот пример окна теста.
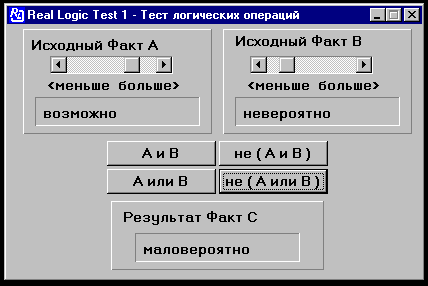
Используя подобный пример, Вы можете подставить факты из реальной жизни и проверить работу логических функций.
Не меняя интерфейсную часть модуля в реализацию операций можно вносить изменения и проверять работу программы.
Например, для операции И можно попробовать формулу
R=(A*B)/(A+B).
На мой взгляд, эта формула занижает оценки, вес которых менее 0.5
Второй пример поясняет работу функций преобразования.
Эти функции используются для того, чтобы привести величины реального мира (длины, объемы, цвета и т.д.) к весу фактов. Например, рост может быть преобразован к системе НИЗКИЙ - СРЕДНИЙ - ВЫСОКИЙ. Для этого используется S-функция (RLSfun в модуле). Значения X1 - самый низкий рост, X2 - самый высокий.
После выполнения логических операций желательно выполнить обратное преобразование. В модуле обратная S-функция названа RLSarg (получить аргумент S-функции).
В примере использованы линейные функции преобразования. Именно они используются чаще всего благодаря своей простоте. Этого в большинстве случаев достаточно, но не всегда правильно работают функции преобразования. Приведенный на рисунке пример преобразует рост человека. Если рост выходит за пределы X1 - X2 (в данном случае задан рост меньше, чем X1), то обратная функция дает неточный результат.
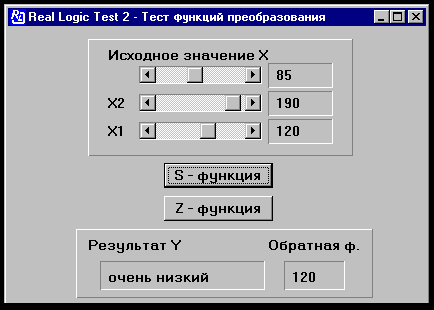
Этого можно избежать, применив степенные или логарифмические функции преобразования. Поиск универсальной формулы для S-функции пока не привел к положительному результату. Вероятно, в различных прикладных областях следует применять различные функции.
Попробуйте для функции преобразования роста использовать формулу
Y = (X-170)^(1/5)/6+1/2.
В формуле 170 - средний рост человека.
Обратное преобразование будет иметь вид:
X = (6(Y-1/2))^5+170
Данные формулы не дают погрешности при многократных преобразованиях между ростом и оценкой.
Проверьте, как поведет себя система, если оценка получена путем вычислений, например задайте значение 1 (самый высокий) и Вы получите рост 400 сантиметров. Я таких людей не встречал.
А что, если позволить экспертным оценкам немного выходить за пределы диапазона 0...1. Тогда и в крайних значениях 0 и 1 все нормально и обратные преобразования не дают погрешностей. Логические операции при этом работают по-старому (min,max).
У меня получились формулы:
Y = (X-170)^(1/3)/6+1/2
X = (6(Y-1/2))^3+170
Функция третьей степени более пологая, чем функция пятой степени и коэффициенты подобраны так, что значение оценки 1 (высокий) соответствует росту около 200 см.
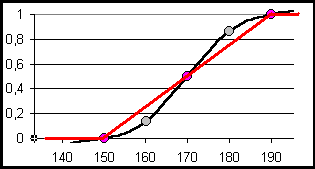
График показывает соотношение линейной и кубической функций преобразования.
Предвижу, что относительно правильности данных функций со мной многие могут не согласиться, (женщины ниже мужчин, китайцы ниже европейцев и вообще каждый оценивает рост другого в сравнении со своим). Еще больше возражений было-бы, если попытаться сформулировать функцию дохода (богатый - бедный). Правительство, назначая зарплату мыслит одними функциями, а учитель, получая ее, вероятно - другими.
Используя S-функцию и логические операции можно представить и другие функции. В тексте модуля присутствует несколько таких функций: V,U,A,P (русская П соответствует больше).
Z-функцию также можно вывести из S-функции при помощи операции NOT, но при этом придется пересчитывать коэффициенты (или задавать зеркальные точки в линейном случае, что не совсем удобно), поэтому Z-функция реализована отдельно.
Материал содержит много спорных моментов и ваши замечания, предложения будут весьма желательны.