
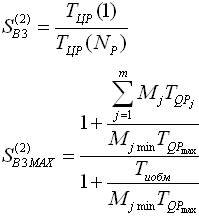
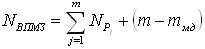

В современных условиях темпы технического прогресса и успехи в решении фундаментальных научных проблем во многом определяются уровнем развития вычислительной техники. В это время общепризнанным является класс фундаментальных научных и инженерных проблем Grand challenges, эффективное решение которых возможно только с использованием мощных вычислительных ресурсов с производительностью сотен Gflops (~1012 операций в секунду) и выше.
Чтобы обосновать потребность в указанной производительности, например, для задач аэрогазодинамики, можно привести сравнительно простой пример расчетов аэродинамических характеристик изолированного крыла. Можно показать, что для получения стационарного решения уравнений Навье-Стокса необходимо выполнить порядка 2•1013 арифметических операции. При использовании современных персональных компьютеров на это будет нужно десятки часов. На практике аэродинамического проектирования по обыкновению нужен не отдельный расчет, а систематический перебор и анализ многих вариантов. Отсюда ясно, что лишь при наличии ЭВМ с производительностью, которая существенным образом превышает показатели персональных компьютеров, численное моделирование может стать реальным инструментом проектирования летательных аппаратов. Единственным способом достижения необходимой производительности в данное время есть использования многопроцессорных вычислительных систем.
Однако, в случае многопроцессорных вычислительных систем достичь высокой производительности при решении реальных прикладных задач оказывается значительно сложнее, чем для традиционных ЭВМ. Основным требованием к алгоритму является наличие внутреннего параллелизма. Это означает, что алгоритм должен составляться из некоторого количества частей, которые могут выполняться одновременно и независимо друг от друга. Следующий принципиальный факт во многом определяет возможность эффективной параллельной реализации алгоритмов. Для многопроцессорных систем время обмена сообщениями между процессорами существенно превышает время доступа к своей локальной памяти и, тем более, время выполнения арифметических операций. Отсюда возникает условие локальности алгоритма - на каждом процессорном элементе (ПЭ) обращение к локальной памяти и выполнение арифметических операций должны происходить значительно чаще, чем обмены со вторыми ПЭ. В конце концов, нужно отметить довольно желательное требование масштабируемости, которая означает способность алгоритма работать на произвольном числе процессоров. На практике это свойство обеспечивает высокую эффективность параллельной реализации и для конкретного числа ПЭ.
На сегодня, благодаря использованию новой высокопроизводительной техники, полученное значительное продвижение в решении вычислительных проблем механики, современной физики, квантовой химии, биологии и по другим направлениям науки.
Моделирование СДС приобретает всё большую актуальность. Для реализации моделей СДС применяются многопроцессорные системы, причём нужно заметить, что вся потенциальная вычислительная мощность такой системы используется не полностью. Для достижения большей продуктивности системы разработчики параллельного программного обеспечения решают проблему распараллеливания программ.
При параллельном моделировании Сетевых Динамических Объектов с Распределёнными Параметрами (СДОРП) решаются системы с большим количеством уравнений. При этом возникает проблема распределения вычислительной нагрузки по процессам.
Сетевые динамические объекты распространены в различных областях науки и техники как класс объектов исследования, проектирования, наблюдения и управления. Реальные сети имеют большое количество элементов, сильное взаимодействие управляемых переменных, нелинейность параметров. При разработке и исследовании динамических систем с помощью вычислительных машин предъявляются определенные требования [1] к математическим моделям. В связи с этим на первый план выходит вопрос о построении параллельных моделирующих сред [2], удовлетворяющих поставленным требованиям, имеющих интерфейс пользователя и способных решать заданные задачи в тесном взаимодействии с пользователем.
Концепция распределенной параллельной моделирующей среды (РПМС) для сложных динамических систем с сосредоточенными и распределенными параметрами была предложена в 1992 г. в рамках научного сотрудничества факультета ВТИ ДонНТУ и института параллельных и распределенных систем (IPVS) Штуттгартского университета (Германия), опубликовано в Asim-докладе [3]. РПМС называется такая системная организация совместного функционирования параллельных аппаратных ресурсов, системного и моделирующего программного обеспечения, которая поддерживает все этапы разработки, реализации и применение параллельных моделей СДС [4].
Главным положением РПМС-концепции является необходимость полнофункциональной разработки параллельных методов и алгоритмов функционирования моделирующего программного обеспечения (Modeling and Simulation Software) для ДСЗП, ДСРП. Анализ показывает, что параллельные системы SIMD- и Mimd-структур 90-х годов имели фирменные языки параллельного программирования, которые базируются на языках Fortran, C, C++, Modula-2 и др. Развитие параллельных вычислительных систем Mimd-архитектуры, объектно-ориентированных подходов стимулировал стандартизацию средств параллельного и распределенного программирования. Так, ANSI и ISO определили С++-стандарты с библиотеками MPI, PVM и Pthreads. Концепция предусматривает обеспечить пользователей и разработчиков параллельных моделей языковыми и системно-организационными средствами, которые по уровню сервиса будут превосходить системы и языки моделирования пятого поколения [5]. В этом направлении проведены разработки относительно обобщения топологий СДС, а комплексы „топологические анализаторы - генераторы уравнений-решатели" транслируют описания СДС уровня предметной области в параллельные программы [4].
Существует 2 варианта реализации третьего уровня распараллеливания [3]. Их сравнение приведено в таблице 1 по следующим критериям:
Равномерность загрузки
Соотношение Nоо/Nобм
Виртуальное ускорение с учетом операций обмена
Схема связи между процессами
Количество Q- и P-процессов
Таблица 1. Сравнение двух вариантов третьего уровня распараллеливания.
| Крітерій | 1 варіант | 2 варіант |
| Равномерность загрузки | Загрузка (QP)j Lj=2Mj=lj/Δξ зависит от количества решаемых уравнений и разброса длин lj веток. неравномерность ΔL=Lmax-Lmin=2(Mjmax-Mjmin), учитывая диапазон длин выработок ШВМ будет существенной. | Каждый из Npj+1 провцессов решает не менее чем Mmin=ljmin/Δξ пар уравнений. Достигнута формализация планирования и равномерного распределения загрузок процессов по предложенному алгоритму. Алгоритм обобщает данные относительно процессов всех ветвей ШВМ. |
| Соотношение Nоо/Nобм | 2Mj≤Nоо/Nобм≤4Mj | 2Mmin≤Nоо/Nобм≤4Mmin |
| Виртуальное ускорение с учетом операций обмена |  | 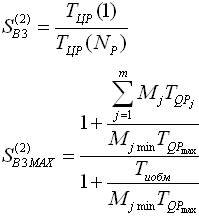 |
| Схема связи между процессами | Предложены виртуальные PQ- и QP-коммутаторы, работа которых организуется таким образом: схема связей между процессами реализуется к началу работы и остается неизменной на весь период моделирования; в i-м цикле вычислений запоминаются компоненты векторов Qj(ih) Pj(ih) и записываются в исходные регистры Q- и P-процессов; все процессы синхронизируются по моменту завершения самого длинного процесса, синхронно для всех Q- и P-процессов активируются команды обмена, в один такт на входах Q- и P-процесов появляются актуальные значения переменных и следующим тактом записываются в память; запускается i+1-й цикл вычислений. На всех уровнях коммутаторы реализуются однотипно на базе переключателей 2х2. | |
| Количество Q- и P-процессов | NВПМЗ=m | 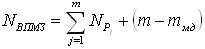 |
Разработка симмодели СДОРП происходит с помощью аппроксимации системы уравнений в частичных производных системой обычных дифференциальных уравнений на основе метода прямых. Сущность метода заключается в том, что каждая ветвь объекта представляется в виде прямой, разделенной на части длиной Δx:

Математическая модель выглядит таким образом [7]:

P(x,t) - давления в і-й ветки системи;
Q(x,t) - расход воздуха в і-й ветки системи;
r - аэродинамическое сопротивление;
r’- регулируемое аэродинамическое сопротивление;
x - пространственная координата;
F - площадь поперечного сечения выработки;
a - скорость звука в воздухе;
ρ - плотность воздуха.
Для того чтобы было удобно использовать численный метод, нужно записать систему уравнений в таком виде [8]:

Такая система уравнений является удобной для использования любого численного метода, например метода Рунге-Кутта или Адамса-Башфорта.
Несмотря на достигнутые успехи в развитии и внедрении ПМС, она остается еще мало исследованным объектом разработки и реализации. Создание параллельной среды, ориентированной на моделирование сетевых динамических объектов с сосредоточенными параметрами позволит повысить дружественность средств моделирования к пользователям и обеспечить эффективную модельную поддержку исследования, проектирования и автоматизации СДОCП.
В данном реферате исследованно текущее состояние проблемы магистерской работы. Также обозначенные направления дальнейшей работы, которые будут проработаны в магистерской работе (разработка MIMD-симулятора). Детально рассмотрен вопрос актуальности и текущего состояния распределенных параллельных моделирующих сред (РПМС).
Основные понятия и термины параллельного программирования. [Электронный ресурс]
http://www.computerbase.de/lexikon/Parallele_Programmierung
Святний В.А. Паралельне моделювання складних динамічних систем // Моделирование - 2006: Международная конференция. Киев, 2006 г. - Киев, 2006. - С. 83-90.
Святний В.А., Молдованова О.В.,Чут А.М.: Стан та перспективи розробок паралельних моделюючих середовищ для складних динамічних систем з розподіленими та зосередженими параметрами.
Schmidt B. Simulationssyteme der 5. Generation - SiP, Heft 1, 1994, S. 5-6.
Бройнль Т. Паралельне програмування: Початковий курс: Навч. посiбник / Переклад з нiм. В. А. Святного. - К.: Вища шк., 1997. - 358 с.
Хьюз К., Хьюз Т. Параллельное и распределенное программирование на С++ / Пер. с англ. – М.: Издательский дом «Вильямс», 2004. – 672 с.: ил.
Moldovanova O.V., Svjatnyj V.A., Feldmann L., Resch M., Küster U.: Problemorientierte parallele Simulationsumgebung. // Научные труды ДонНТУ, серия «Информатика, кибернетика и вычислительная техника», вып. 93. – Донецк, 2005. – С. 145–150.
Святний В.А. Паралельне моделювання складних динамічних систем // Моделирование – 2006: Международная конференция. Киев, 2006 г. – Киев, 2006. – С. 83–90.
Гусєва Г.Б., Молдованова О.В. MIMD-паралельний вирішувач рівнянь для мережного динамічного об’єкту з розподіленими параметрами // Проблемы моделирования и автоматизации проектирования динамических систем: Сб. научн. тр. ДонНТУ, вып.6, Донецк, 2007.
Бондарева Е. С. Генератор уравнений параллельной моделирующей среды для технологических процессов // Проблемы моделирования и автоматизации проектирования динамических систем: Сб. научн. тр. ДонНТУ, вып.6, Донецк, 2007.