УДК 681.124.077

Информационные аспекты автоматики (автоматов)

Лушпенко В. С. ст. гр. СП-04 Б

рук. Иванова Л. И.

Донецкий государственный технический университет

Любой логической переменной можно поставить в соответствие участок электрической цепи, который будет проводить ток при и не будет при . Тогда последовательному соединению элементов будет соответствовать логическое умножение переменных, а параллельному – логическое сложение. Чтобы управлять состоянием элемента цепи, можно использовать переключатель – если он включен, , если он выключен – . Функцию ­– отрицание – можно реализовать с помощью размыкающего реле (если контакт замкнут, то через электромагнит идёт ток. он притягивает и размыкает контакт , если разомкнут, то замкнут). Аналогично можно реализовать функцию ­– с помощью замыкающего реле. Понятно, что, используя несколько электромагнитов, можно с помощью одного „управляющего” контакта контролировать состояние нескольких других контактов. Вместо реле можно использовать любое другое аналогичное по действию устройство (механические переключатели с фиксированным количеством положений, радиолампы, полупроводниковые элементы и др.).

Поскольку любую логическую функцию можно задать формулой, составленной с помощью булевых операций, каждая такая функция может быть реализована с помощью электрической схемы, составленной из комбинаций последовательных и параллельных соединений контактов и реле. Такие схемы называются контактно-релейными. Множество таких схем можно превратить в булеву алгебру, если их произведение определить как результат их последовательного соединения, а сложение – как результат параллельного соединения. Операция отрицания осуществляется с помощью какого-либо инвертора (реле, транзистор и т. п.). при этом две схемы считаются одинаковыми, если они одновременно проводят или не проводят ток при одинаковом состоянии управляющих контактов. Построенная таким образом алгебра схем изоморфна алгебре логики, а это позволяет использовать для схем средства алгебры логики.

Впервые на подобную возможность указал известный физик Пауль Эренфест в 1910 г., но систематические исследования в этой области начались а конце 30-х гг. после работ американца К. Шеннона (который затем прославился как „отец теории информации”) и советского физика В. И. Шестакова.

Для конструирования схемы, обеспечивающей включение и выключение лампы любым из двух выключателей требуется, чтобы переключение любого выключателя зажигало лампу, если она не горит и гасило в противоположном случае независимо от положения второго выключателя. Сопоставим выключателям переменные и , а лампе переменную . Если оба выключателя выключены, т. е. и , то лампа не горит (). Если мы включили один выключатель ( или ), - лампа загорается. Если мы включаем второй выключатель, лампа гаснет.

Таблица, описывающая зависимость .

Функция, соответствующая такой таблице имеет вид .

Электрическая схема для такой функции:

В современной технике широко используются автоматы. С точки зрения математики – это устройства для преобразования информации. В данной работе рассматриваются конечные автоматы. Это значит, что на вход подаётся и на выходе выводятся конечные порции алфавитно-цифровой информации; информация на выходе зависит не только от входной информации, но и от внутреннего состояния автомата; автомат может иметь лишь конечное число внутренних состояний. Поскольку любая информация, в т. ч. и алфавитно-цифровая может быть представлена в двоичном виде (например, азбука Морзе), можно считать, что на вход автомата подаётся набор нулей и единиц – , а на выходе выводится другой набор нулей и единиц – . Получив на вход сигналы , автомат через некоторое время („задержка”) выдаёт сигналы и меняет своё внутреннее состояние. Если же величины зависят только от входных данных , то говорят, что автомат не имеет памяти. Автоматы без памяти также называют комбинационными схемами.

В том случае, когда автомат не имеет памяти, величины являются логическими функциями от входных данных . Такой автомат можно реализовать с помощью m контактно-релейных схем – каждая схема будет реализовывать функцию одной выходной переменной. Информация на входе задаётся включением или выключением i-го контакта, который соответствует . Считается, что принимает значение 1, если i-я схема пропускает ток и 0, если нет. Поскольку с помощью контактно-релейных схем можно реализовать любую логическую функцию, в принципе, можно собрать любой автомат без памяти, если известно, как он должен функционировать.

Однако автомат, синтезированный с помощью основных правил формирования логических функций получается весьма громоздким и сложным. Поэтому весьма логично для упрощения внутреннего устройства автомата упрощать полученную логическую функцию средствами алгебры логики.

Пример. Определить бит переноса при суммировании трёх битов.

Таблица.

Функция имеет вид: .

Электрическая схема, соответствующая этой функции:

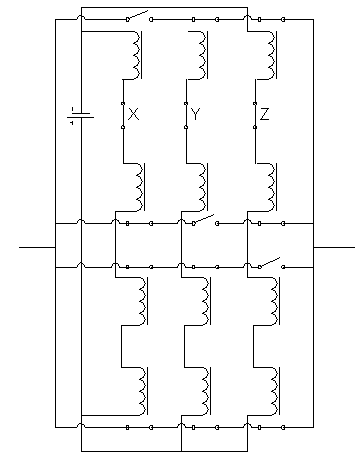
Упростим её:

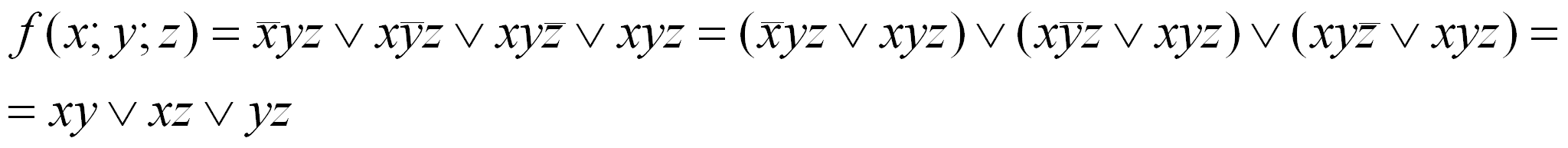В результате упрощений вместо 3 отрицаний, 8 умножений, 3 сложений получили 2 сложения и 3 умножения.

Схема, соответствующая этой функции:

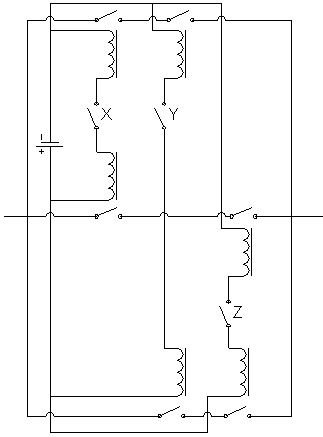
Современные ЭВМ являются типичными примерами автоматов с памятью. Важнейшие компоненты ЭВМ – ка­налы ввода – вывода, арифметическое устройство и запоминающее устройство. В первом приближении арифметическое устройство, пред­назначенное для арифметической и логической обработки данных, можно рассматривать как автомат без памяти, который получает информацию, как через каналы ввода-вывода, так и из запоминающе­го устройства.

В современных вычислительных машинах вместо контактно-релейных схем используются полупроводниковые элементы, но матема­тический принцип синтеза остается прежним. А в первых вычисли­тельных машинах (в 40-х годах) использовались именно контактно-релейные схемы. В серийных машинах первого поколения (50-е годы) использовались радиолампы, в машинах второго поколения применя­лись полупроводниковые элементы – транзисторы, резисторы и т. п.; в современных ЭВМ применяются так называемые «интегральные схе­мы». Однако булева алгебра неизменно остается важным орудием син­теза и анализа автоматов.

Отметим, что булевы операции и идеи алгебры логики широко ис­пользуются и в современных языках программирования (Алгол, Фор­тран и др.), помогающих управлять работой ЭВМ.