Конечный автомат представляет собой наиболее общую математическую модель цифрового устройства или цифровой системы. Поэтому очень важно при разработке различных цифровых устройств и систем применять эффективные методы синтеза конечных автоматов. В то же время, реализованные в известных пакетах автоматизированного проектирования (фирм Altera, Xilinx и других) методы синтеза основаны на традиционных подходах, которые не позволяют эффективно использовать архитектурные возможности новой элементной базы.
Традиционно синтез управляющего автомата (УА) выполняется по заданной базовой структуре, а оптимизация схемы достигается за счет ряда методов, таких как оптимальное кодирование состояний, выделение подуровней в комбинационных схемах и трансформация кодов объектов. В то же время в операционном автомате ветви алгоритма могут реализовываться параллельно для достижения максимального быстродействия операционного автомата (ОА). При традиционной реализации УА Мура управление таким ОА осуществляется несколькими управляющими автоматами по иерархическому принципу. Что в свою очередь уменьшает быстродействие УА [1].
Предполагается применить унитарное кодирование состояний УА Мура в виде сети Петри, что позволит исключить традиционный синтез автомата по таблице переходов. А это, в свою очередь, позволит добиться минимизации логической схемы автомата с целью повышения его быстродействия. Также, такой синтез позволит реализацию параллельного управления.
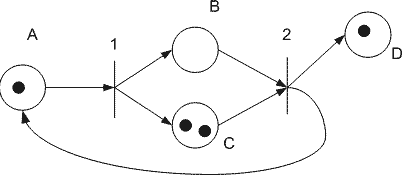
еть Петри представляет собой двудольный ориентированный граф, состоящий из вершин двух типов – позиций и переходов, соединенных между собой дугами, при этом вершины одного типа не могут быть соединены непосредственно. В позициях размещены метки (маркеры), способные перемещаться по сети. Событием в сети Петри называется срабатывание перехода, при котором метки из входных позиций перемещаются в выходные позиции. Переход срабатывает, если имеется как минимум 1 метка в каждом из его исходных позиций [2].

Рисунок 1 - Пример простой сети Петри
Исходя из этого, произвольная граф-схема алгоритма для УА является частным случаям сети Петри с меткой, соответствующей текущему состоянию автомата и метками функций возбуждения.
Рассмотрим реализацию УА Мура в виде сети Петри, заданного на рис. 2. Обратим внимание на то, что ветви алгоритма а3->a4 и a6 –>a7 выполняются параллельно. Для реализации схемы данного автомата на FPGA необходимо заменить компоненты сети Петри на рисунке 3 их функциональными аналогами: позиция состояния автомата – D – триггером, перехода – элементом "И", множество входов в позицию объединяется элементами "ИЛИ". Дугам, соединяющим места и переходы, соответствуют обычные электрические соединения. На рис. 4 показана функциональная схема УА, полученная для ГСА из сети Петри.
Для того щоб підібрати оптимальний варіант розбивки на ЛПС для конкретного алгоритму необхідно синтезувати досить велику кількість варіантів і проаналізувати отримані результати.
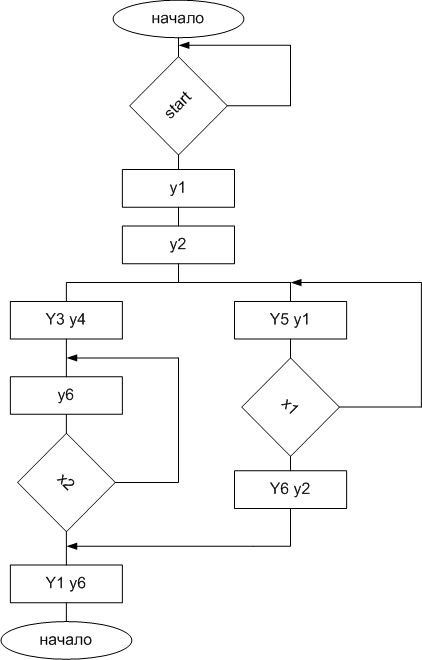
Рисунок 2 - Исходная граф-схема алгоритма

Рисунок 3 - Сеть Петри для исходной ГСА
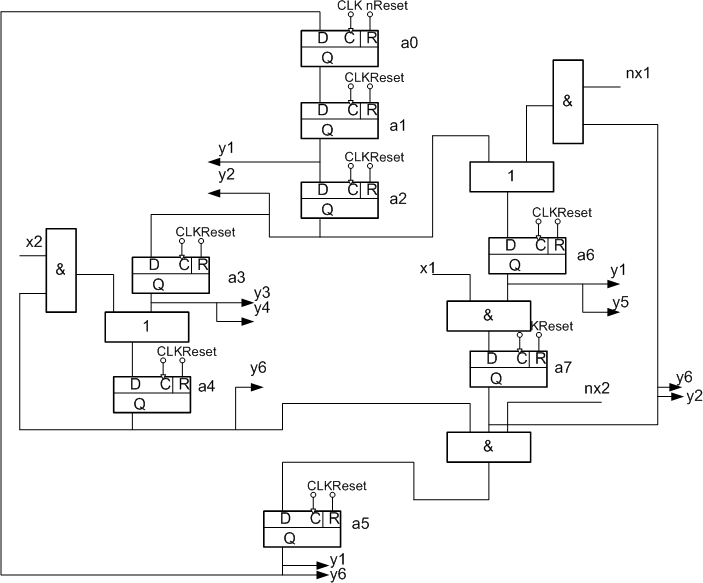
Рисунок 4 - Функциональная схема УА Мура по ГСА
По сигналу Reset="1" все триггера сбрасываются в "0", а триггер a0 в 1, что соответствует исходному состоянию, поскольку при этом не вырабатывается никаких управляющих сигналов (сигнал start). В каждом такте CLK в один или несколько (в параллельных ветвях) триггеров записывается "1", что соответствует переходу из одного состояние в другое. При этом в триггер, из которого происходит запись "1", записывается "0". Для обеспечения корректной работы схемы сигнал reset должен иметь длительность не более одного такта и вырабатываться один раз при запуске УА.
Далее полученная схема описывается на языке VHDL для последующего автоматического синтеза и окончательной имплементации на FPGA.