Barkalov A.A., Krasichkov A.A., Khalid Barakat. Synthesis of the Moore FSM with the unitary states coding on FPGA. The method of synthesis of the Moore FSM with unitary state’s coding on FPGA is offered. The method is based on the automata realization on the flowchart as a Petri network. The features of realization of the Moore FSM on FPGA are considered. The method of synthesis of the Moore automata is given.
Общая постановка проблемы. В настоящее время цифровые устройств, в частности, управляющие автоматы (УА) строятся на ПЛИС с архитектурой FPGA [1]. Функциональный базис FPGA представляет собой множество идентичных конфигурируемых логических блоков (КЛБ) с R входами, реализующих произвольную булеву функцию R аргументов. В зависимости от модели микросхемы FPGA R=2,5 [1]. Ввиду особенностей функционального базиса FPGA, предпочтение отдается УА с жесткой логикой. В работе [2] предлагается метод синтеза УА Мили на FPGA, основанный на функциональной декомпозиции. Предложенный метод, однако, приводит к невыгодной реализации схемы дешифратора на КЛБ при большом числе состояний УА. В работе [3] описаны методы декомпозиции, позволяющие сократить число КЛБ реализуемых функций, однако, как показали проведенные исследования, схема дешифратора УА оптимизируется незначительно. В работе [4] предложены методы синтеза комбинационных схем УА в виде многоуровневых структур, что всегда позволяет сократить число аргументов реализуемых функций, однако, за счет последовательного включения уровней увеличивается задержка в схеме УА. Следовательно, при реализации известных структур УА с жесткой логикой число переменных значительно превосходит R, что приводит к невыгодной реализации схемы на вентильном уровне и снижению быстродействия.
Таким образом, нерешенной проблемой является минимизация логической схемы автомата с целью повышения его быстродействия.
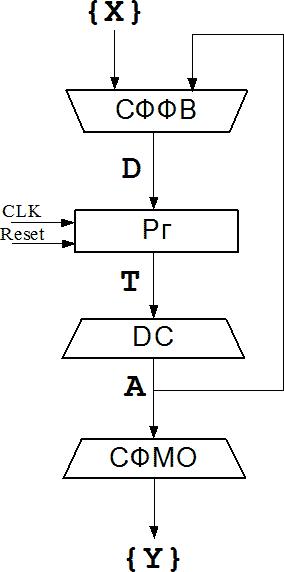
На рис. 1 приведена базовая структура УА Мура, в которую входят регистр состояния (Рг), комбинационные схемы для формирования функций возбуждения (СФФВ), микроопераций (СФМО), а также дешифратор состояний (DC).
Традиционно синтез УА выполняется по указанной базовой структуре, а оптимизация схемы достигается за счет ряда методов, таких как оптимальное кодирование состояний, выделение подуровней в комбинационных схемах и трансформация кодов объектов [3,4].
В FPGA в состав каждого КЛБ входит D-триггер, что позволяет наиболее оптимально реализовывать на FPGA схемы с древовидной структурой и большим числом состояний, в частности, сети Петри [5]. В данной работе предлагается применить унитарное кодирование состояний УА Мура, что приведет к вырождению схемы дешифратора и уменьшит число аргументов СФФВ. Также предлагается представление схемы УА Мура в виде сети Петри, что позволит исключить традиционный синтез автомата по таблице переходов.

Рис. 1. Базовая структура УА Мура
Модель сети Петри является принципиально асинхронной и служит для отображения и анализа причинно-следственных связей в системе. Для привязки к определенным моментам времени тех или иных переходов используются события [6].
Простой сетью Петри называется набор N=(S,T,M,P,F), где:
Условия в пункте 5 говорят, что для каждого перехода t ∈ T существует единственный элемент <S', t, S"> ∈ F, задающий для него входное множество мест S' и выходное множество S".
Сеть Петри имеет наглядную форму представления в виде графа, который включает четыре базовых элемента: позиции (места), переходы, дуги и метки. На рис. 2 приведен пример такого графа, задающего простую сеть Петри с тремя местами, тремя метками и двумя переходами.
Функционирование сети заключается в перемещении меток m1-m3 по дугам между местами S1-S3 и формировании событий. Переходы t1-t2 задают условия перемещений меток из мест S1 и S3. Исходное размещение меток по местам является начальным условием и может быть произвольным.

Рис. 2. Пример простой сети Петри
Исходя из этого, произвольная граф-схема алгоритма (ГСА) для УА, является частным случаем сети Петри с одной меткой, которая соответствует текущему состоянию автомата. Множество мест S соответствует множеству состояний автомата, множество переходов t – множеству условных вершин, множество событий – множеству наборов управляющих сигналов.
Таким образом, произвольный УА может быть представлен в виде сети Петри. В том случае, если события возникают по наличию метки в определенном месте, сеть отображает поведение УА Мура. Если события формируются во время перемещений меток между местами, в зависимости от переходов, то сеть отображает поведение автомата Мили.
Решение задач и результаты исследований. Рассмотрим реализацию УА Мура в виде сети Петри, заданного ГСА на рисунке 3.
Данная ГСА соответствует сети Петри с пятью состояниями – a0-a4, четырьмя переходами с тремя условиями – Start,x1,x2, и четырьмя событиями – y1-y4 (Рис. 4).
Сеть функционирует следующим образом. В исходном состоянии метка находится в месте a0. При этом не формируется никаких событий. Данное место является ждущей вершиной. Переход метки в место a1 осуществляется через первый переход только при выполнении условия Start=1. Пока метка находится в месте a1, действительно событие y1. Из a1 происходит безусловный переход в место a2, в котором действительны события y2 и y3. Из a2, благодаря двум переходам (по x1 и x2) возможны три варианта перемещений – в a2, a3 или a4. Далее функционирование сети происходит аналогичным образом и однозначно соответствует выполнению алгоритма управления, заданного исходной ГСА. Данная сеть не имеет тупиковых состояний, поскольку соответствует замкнутому алгоритму УА. Поэтому переходы в место a0 приводят к повторному выполнению алгоритма, начиная с ждущей вершины. В случае необходимости однократного выполнения алгоритма по сигналу Start, достаточно удалить все связи конечных вершин сети с вершиной a0.

Рис. 3. Исходная граф-схема алгоритма
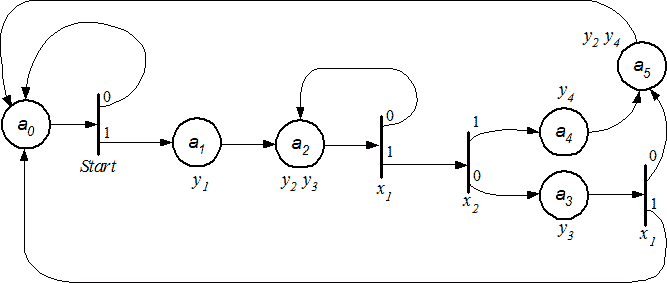
Рис. 4. Сеть Петри для исходной ГСА
Для реализации схемы данного автомата на FPGA, необходимо заменить компоненты сети на рис.4 их функциональными аналогами. Если в качестве места (состояния) использовать D-триггер, то меткой будет служить сигнал логической единицы, записанной в триггер текущего состояния. Множество входов в каждое состояние объединяется элементом "ИЛИ" и подается на соответствующий триггер. Функцию перехода выполняет стандартный однобитовый демультиплексор на два выхода, управляемый одним условием. События (управляющие сигналы) формируются как логическое "ИЛИ" выходов соответствующих им состояний (триггеров). Дугам, соединяющим места и переходы, соответствуют обычные электрические соединения. На рис.5 показана функциональная схема УА, полученная из сети Петри для ГСА Г.

Рис. 5. Функциональная схема УА Мура по ГСА Г
Схема работает следующим образом. По сигналу Reset="1" все триггера сбрасываются в "0", что соответствует состоянию автомата a0, поскольку при этом не вырабатывается никаких управляющих сигналов. При появлении сигнала Start=1, в триггер a0 по переднему фронту синхросигнала CLK записывается логическая "1", что разрешает дальнейшее функционирование схемы УА по заданному алгоритму. Такая реализация позволяет не использовать демультиплексор, который соответствует на рис. 4 переходу с условием Start. В каждом такте CLK в один из триггеров записывается "1", что соответствует переходу из одного состояние в другое. При этом в триггер, из которого происходит запись "1", записывается "0". Для обеспечения корректной работы схемы сигнал Start должен иметь длительность не более одного такта и вырабатываться один раз при запуске УА.
Далее полученная схема описывается на языке VHDL для последующего автоматического синтеза и окончательной имплементации на FPGA [2].
Преимуществом такой реализации УА на FPGA являются:
Формализация синтеза и анализа таких схем УА позволила автоматизировать генерацию конечного VHDL-кода по исходной ГСА, заданной текстовым файлом. Синтез, окончательная оптимизация размещения схемы по КЛБ и оценка параметров полученной реализации выполняется уже непосредственно в САПР. При имплементации данной схемы УА на FPGA серии Spartan-II использовано 12 четырехвходовых КЛБ и 5 триггеров (в составе КЛБ). Максимальная задержка сигналов в схеме составила 6,5 нс. При реализации данной логической схемы УА на других семействах FPGA возможны другие показатели быстродействия и аппаратурных затрат.