Баркалов А.А., Красичков А.А., Выприцкая П.А. Методы декомпозиции ГСА на подграфы для синтеза автоматов Мили на счетчике. В статье рассматриваются управляющие автоматы Мили на счетчике, оптимизация быстродействия и аппаратных затрат при их использовании, необходимость создания системы автоматизированного проектирования (САПР) этих автоматов. В качестве начального этапа создания САПР разработаны алгоритмы разбиения ГСА на ЛПС двух типов, также обнаружена закономерность, позволяющая применить алгоритм разбиения одного типа для получения разбиения другого.
Баркалов О.О., Красічков О.О., Випріцька П.О. Методи декомпозиції ГСА на підграфи для синтезу автоматів Мілі на лічильнику. В статті розглядаються керуючі автомати Мілі на лічильнику, оптимізація швидкодії та апаратних затрат при їхньому використанні, необхідність створення системи автоматизованого проектування (САПР) цих автоматів. Як перший етап створення САПР розроблені алгоритми розбивання ГСА на ЛПС двох типів, також знайдена закономірність, що дозволяє використати алгоритм розбивання одного типу для отримання розбивки іншого.
Barkalov A.A., Krasichkov A.A., Vypritskaya P.A. Methods of flowchart decomposition on sub-charts for Mealy FSM synthesis with counter. In article the Mealy FSM on counter, optimization of speed and hardware expenses are considered at their use, necessity of CAD creation for these automata’s. As the initial stage of CAD algorithms creation the splitting flowchart on linear state sequences (LSS) of two types are developed, rule allowing to apply algorithm of splitting of one type for reception of splitting another also is found out.
У наш час відбувається автоматизація процесів у всіх сферах знань навколишнього світу. У деяких сферах застосування ця автоматизація зводиться до створення програмного забезпечення для персонального комп'ютера, але в більшості випадків вимагає створення спеціалізованих ЕОМ. Для організації роботи ЕОМ, як одна з її складових, необхідний керуючий автомат. У його функції входить формування керуючих сигналів, на основі деякого алгоритму для операційної частини ЕОМ.
Алгоритм управління системи задається кодом управління, що надходить в КА із зовнішнього середовища. Алгоритм управління ОА називається мікропрограмою і реалізується керуючим автоматом. Однією з основних проблем при створенні спеціалізованої ЕОМ є пошук компромісу між швидкодією, вартістю і універсальністю КА. Також важливим є час проектування і реалізації схеми КА.
Як відомо, КА з жорсткою логікою виграють за швидкодією перед автоматами з програмованою логікою, але мають жорстку структуру і не можуть бути змінені. ПЛІС дозволяють замінити весь пристрій конфігурований на мікросхему. Таким чином з'являється можливість створювати перепрограмовані КА з жорсткою логікою [1].
Доведено, що для алгоритмів, в яких не менше 75% вершин складають операторні, оптимізація апаратних витрат в схемі автомата можлива за рахунок заміни регістра пам'яті лічильником. [2]
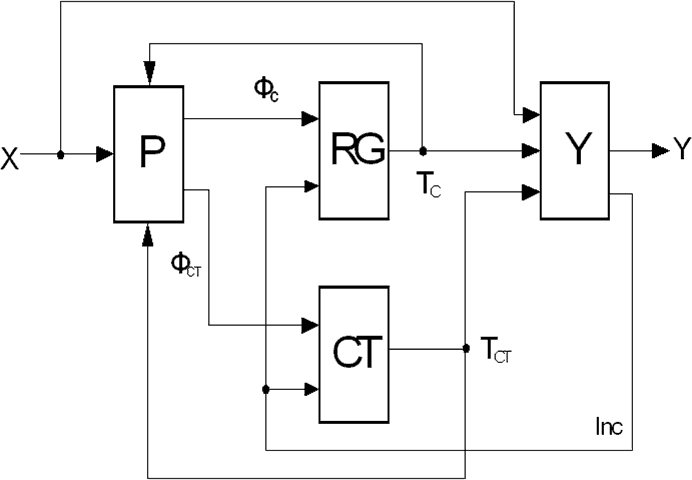
Для використання лічильника запропоновано ГСА розподілити на підграфи – лінійні послідовності станів (ЛПС). Таке розбивання ГСА дозволяє використовувати подвійну нумерацію станів вигляду: <номер ЛПС> : <номер вершини усередині ЛПС>. Автомат Мілі, побудований з використанням розподілення ГСА на ЛПС, в роботі [3] запропоновано називати РС1R-автоматом (рис. 1).
При переході до чергової ЛПС, по сигналу Inc=0 в регістр RG заноситься код ФC ЛПС αg, а в лічильник СТ код ФCT стану am усередині ЛПС αg. Адресація чергового стану am+1 усередині ЛПС αg відбувається шляхом інкременту лічильника по сигналу Inc=1, при цьому значення ФСТ і ФС не визначені, а код стану автомата визначається парою <ТС,ТСТ>.

Рис. 1 – Структура РС1R-автомата
На регістр і на лічильник поступають також сигнали синхронізації (Clосk) і скидання (Reset), не вказані в структурі автомату.
Автомати, при синтезі яких використовується один із зазначених типів ЛПС в роботі [3] запропоновано називати відповідно РС1R1, РС1R2, РС1R3, РС1R4.
Для того щоб підібрати оптимальний варіант розбивки на ЛПС для конкретного алгоритму необхідно синтезувати досить велику кількість варіантів і проаналізувати отримані результати.
Зробити це «вручну» навіть для порівняно невеликих ГСА вимагає значного часу й не гарантує відсутності помилок, тому актуальним є створення програмного засобу автоматизації синтезу PC1R-автоматів.
Першим кроком створення системи синтезу автоматів буде розробка методів розбивки ГСА на ЛПС різних типів.
Очевидно, що для кожного типу ЛПС, методи розбивки ГСА будуть різними. Найпростішим буде розбивання ГСА на ЛПС4.
Для того, щоб розбити ГСА на ЛПС інформація про керуючі сигнали, що формуються при переходах, та про зовнішні умови, за якими відбуваються переходи, неважливі. Важливою є лише топологія вихідної ГСА. Для полегшення сприйняття ГСА, пропонується замінити її графом переходів, де вершини – це стани ГСА, ребра – переходи між ними.
Як було зазначено вище, ЛПС4 може мати лише один вхід, та один вихід. Слід пам’ятати, що вхід та вихід – це вершини графу, а не переходи. На рис. 2 наведено граф переходів, поділений на ЛПС4.
Розглянемо детальніше отриману розбивку.
Вони наведені на рис. 3.
Як видно з рисунку 2, вершина графу переходів типу 4 може бути в ЛПС4 лише єдиною, тому що одночасно є і входом і виходом ЛПС. Вершина типу 3 може бути в ЛПС лише першою, а вершина типу 2 лише останньою. Таким чином, усі вершини типу 4 автоматично стають окремими ЛПС. Усі вершини, до яких здійснюється перехід з вершин типів 2 та 4 стають початком ЛПС. Формування поточної ЛПС закінчується тоді, коли відбувається перехід з вершини вже включеної до поточної ЛПС у вершини типів 2, 3 або 4, при цьому вершина типу 2 включається до поточної ЛПС, а вершини типів 3 та 4 – ні.
З усього вищезазначеного слідує, що розбивка на ЛПС4 є однозначною і може бути виконана лише одним способом, а це означає, що алгоритм розбивки буде послідовним.
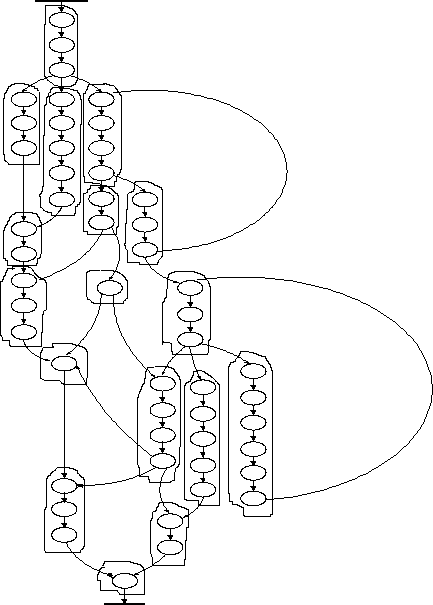
Рис. 2 – Граф переходів, поділений на ЛПС4

Рис. 3 – Типи вершин графу переходів
Тепер розглянемо розбивку графу переходів на ЛПС2. Ці ЛПС відрізняються від вищерозглянутих тим, що вони можуть мати декілька виходів.
Перед початком розбивання графу переходів на ЛПС2 пропонується зробити розбивку на ЛПС4 та замінити граф переходів графом ЛПС4, де вершини – це ЛПС4, ребра – переходи між ними, про кожну вершину такого графу зберігається інформація про кількість станів у цій ЛПС.
На рисунку 4 наведено граф ЛПС4. Цей граф повністю зберігає якості графу переходів та значно скорочує його розміри. При такій заміні зберігаються також типи вершин.
При розбиванні на ЛПС2 вершини типів 3 та 4 можуть бути в ЛПС лише першими. Для безлічі вершин, перехід до яких здійснюється з вершини типу 2 або 4, одна буде приєднана до попередньої, а усі інші стануть початковими для наступних ЛПС.
Оскільки вершини типів 2 та 4 можуть бути не останніми в ЛПС2, то виникає варіантність у виборі вершини, яку приєднати до попередньої, якщо вона типу 2 або 4. Потрібно визначити умови, за якими можна буде здійснювати той чи інший вибір.
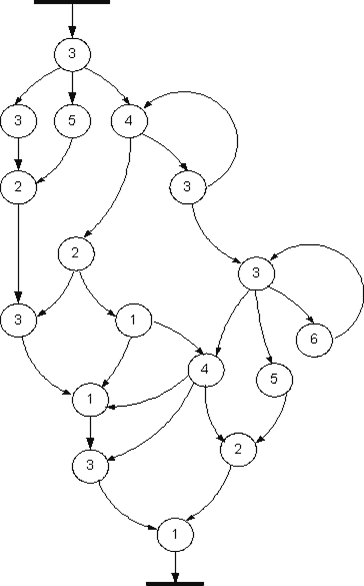
Рис. 4 – Граф ЛПС4
Таким чином, необхідно мінімізувати кількість ЛПС, та при незмінній їх кількості мінімізувати довжину найбільшої ЛПС. Але якщо виконувати розбивання за всіма правилами, та навмисно не розбивати ЛПС там де це не потрібно, кількість ЛПС буде величиною постійною, яка не залежить від варіанту розбивання. Таким чином мінімізувати потрібно лише довжину ЛПС. Це можна зробити якщо обираючи яку вершину приєднати до ЛПС обирати ту, що дасть меншу довжину ЛПС.
На рис. 5 наведено граф ЛПС4, розбитий на ЛПС2.
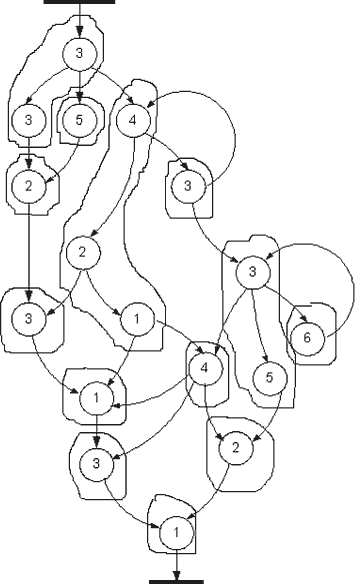
Рис. 5 – Граф ЛПС4
Перейдемо до розбивання графу переходів на ЛПС3. Ці ЛПС можуть мати декілька входів та лише один вихід.
При розбиванні на ЛПС3 вершини типів 2 та 4 можуть бути в ЛПС лише останніми. Для безлічі вершин, перехід з яких здійснюється до вершини типу 3 або 4, вона буде приєднана до однієї з попередніх.
При дослідженні особливостей цього розбивання було виявлено таку закономірність: якщо транспонувати граф, тобто інвертувати усі його зв’язки, для розбивання графу на ЛПС3 стає застосовним алгоритм розбивання на ЛПС2, лише з тією різницею, що граф може мати декілька входів. Потрібно лише замінити перший блок алгоритму формуванням списку перших вершин. Таким чином алгоритм розбивання на ЛПС2 стає універсальним, що значно спрощує подальшу розробку системи автоматичного синтезу автоматів.