Источник: Комп'ютерний моніторінг та информаційні технології - 2009 / Матеріали V науково-технічної конференції студентів, аспірантів та молодих науковців. - Донецьк, ДонНТУ - 2009, с. 262-264.
В настоящее время семейство функий-анализаторов, названных вейвлетами, начинает широко применяться в задачах распознавания образов, при обработке и синтезе различных сигналов, например, речевых, при анализе изображений, для упаковки (свертки) больших объемов информации и во многих других случаях. Однако они еще недостаточно широко известны исследователям, занимающихся анализом данных [2]. Именно поэтому была написана настоящая работа, позволяющиая понять и разобраться в сущности вейвлет-преобразования, при помоши основных математических формул и наглядных образов.
Термин «вейвлет» был впервые введен специалистом по сейсмографии Морле (J.Morlet) в 80-х годах в связи с анализом свойств сейсмических и акустических сигналов. В переводе с английского буквально означает «короткая (или маленькая) волна» [1].
Вейвлеты представляют собой функции, обладающие некоторыми важными свойствами, среди которых следует выделить возможность переноса по времени и масштабируемость.
Рассмотрим вейвлет типа «мексиканская шляпа» (MHAT, «Mexican HAT»), являющийся второй производной функции Гаусса. Его временной образ задается выражением:
График MHAT вейвлета c различными значениями масштаба и переноса по времени изображен на рис. 1.
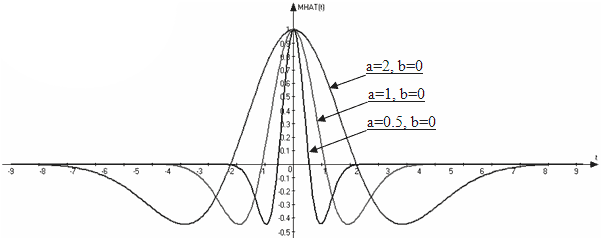
Хорошо видно, что данный вейвлет напоминает затухающее синусоидальное колебание. Причем площадь (над осью времени и под ней) равна нулю. Именно эта особенность позволяет отнести временную зависимость MHAT к вейвлетам.
Можно представить вейвлеты как некоторые волновые функции, способные осуществлять преобразование Фурье не по всей временной оси, а локально по месту своего расположения.
Процесс разложения произвольного входного сигнала в виде совокупности вейвлетов получил название «прямое вейвлет-преобразование» (ПВП). Используемые при этом вейвлеты должны обладать следующими важными свойствами [1]:
При ПВП выполняется задача вычисления вейвлет-коэффициентов. Формально вычисление она реализуется следующим способом:
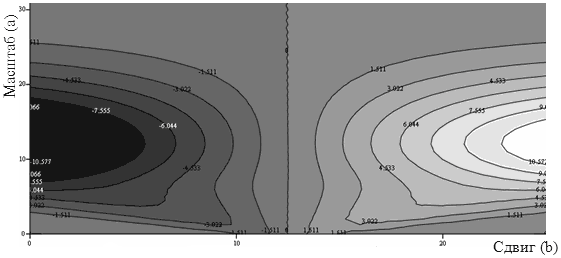
Для примера, выполним прямое вейвлет-преобразование функции, имеющей вид бесконечных симметричных прямоугольных импульсов, а затем полученные коэффициенты представим в виде поверхности. Линии уровней полученной поверхности изображены на рис. 2. Полученный графический образ в дальнейшем может использоваться в процессе распознавания изображения и решения задачи определения его соответствия определенному сигналу.
Теория вейвлетов является той базой, основой, эффективным инструментом, который позволяет решить множество практических задач. Основной областью применения вейвлетных преобразований является анализ и обработка сигналов и функций, когда результаты анализа должны содержать не только общую частотную характеристику сигнала, но и сведения об определенных локальных характеристиках и особенностях сигнала.