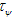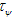до Этот вейвлет дискретизирован периодом выборки данныхИсточник: http://www.asel.udel.edu/icslp/cdrom/vol4/356/a356.pdf
В этой работе рассматривается целесообразность вейвлет преобразований при распознавании фонем. Рассматриваются как дискретное вейвлет преобразование (DWT), так и дискретное непрерывное вейвлет-преобразование (SCWT). Вейвлет преобразование используется в качестве процесса, который вычисляет вектор характеристик для дикторонезависимого распознавателя фонем. Результаты были просчитаны для части TIMIT-базы, состоящей из 30293 фонем для обучения и 14489 фонем для проверки. Предполагаемые результаты испытаний: SCWT дает значительно больший коэффициент верно распознанных фонем чем DWT. С другой стороны, улучшение SCWT с помощью Mel-scale кепстральных коэффициентов, даст незначительный прирост качества распознавания.
Теория вейвлет преобразований (WT) предоставляет альтернативный инструмент для анализа кратковременного квазистационарного сигнала, такого как речь, по сравнению с традиционным кратковременным Фурье преобразованием (STFT). WT широко применяется в различных задачах по распознаванию речи [16, 8, 9, 7, 3].
Скалограмма, получаемая при использовании WT и спектрограмма - при использовании STFT, были сравнены визуально [6, 11, 12, 9, 1]. Было замечено, как частотные, так и гармонические составляющие речи хорошо отображаются на скалограмме. В связи с этим можно сделать предположение, что WT может быть использован для анализа речи. В [5], непрерывное вейвлет-преобразование было использовано в дикторонезависимой системе распознавания изолированных слов, и был получен процент ошибок распознавания в диапазоне от 1.6 % до 6.2 %. В работе [10] было использовано дискретное вейвлет-преобразование (DWT) с небольшим дикторозависимым словарем. Было показано, что DWT демонстрирует явно лучшие результаты чем линейное кодирование (LPC) для неголосовых звуков. Однако, неясно, может ли WT улучшить распознавание на фонетическом уровне. Цель данного исследования состоит в том, чтобы сравнить и CWT и DWT с Mel-scale кепстральными коэффициентами и выявить их возможности в дикторонезависимой системе распознавания фонем.
Вейвлет преобразование - непараметрический инструмент анализа, который позволяет локализировать как временную, так и частотную характеристики.
Главное различие между STFT и WT заключается в том, что STFT - метод анализа с постоянной полосой пропускания, в то время как WT - Q-постоянный метод анализа, который напоминает звуковые фильтры.
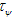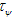Вейвлет коэффициенты вычисляются путем определения корреляции между каждым вейвлетом и сигналом. Реализацию непрерывного вейвлет преобразования называют дискретным CWT (SCWT), который широко используется при анализе речевого сигнала [6, 12, 11, 5, 1]. В SCWT материнский вейвлет является усеченным в области от - до Этот вейвлет дискретизирован периодом выборки данных
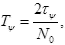
где N0 - число отсчетов, которое дает достаточное разрешение при наименьшем масштабе (самая высокая частота).
Масштабирование дискретного материнского вейвлета достигается путем изменения периода осуществления выборки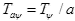 
. Параметр масштаба, a>= 1, может иметь любое значение, при котором вид результата еще не будет слишком разреженным. Параметр сдвига зафиксирован константой b0, чтобы избежать нерегулярной выборки. Тогда SCWT определяется так
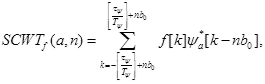
где
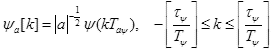
с его частотной характеристикой, полученной по формуле
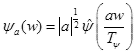
SCWT осуществляется просто линейной фильтрацией [12, 11]. Часто параметр масштаба дискретизируется путем выбора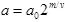 
, где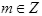 
и V - число голосов на октаву.
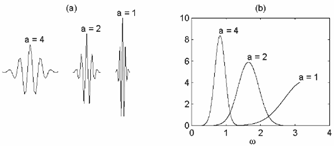
DWT определяется также как SCWT, за исключением того, что a и b ограничены значениями кратными двум, то есть,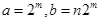 
, где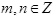 
. В результате, DWT намного грубее чем SCWT, но он может быть очень эффективно реализован быстрым вейвлет преобразованием (FWT), основанным на кодировании подгрупп.
Этот раздел описывает окружающую среду, в которой были сделаны наши тесты распознавания фонем.
Наши тесты распознавания фонем были выполнены прототипе TIMIT базы данных (версия 1988 г.). Были использованы только DR1, DR2 и DR3 области. Набор голосов дикторов для обучения состоит из 30 женских голосов и 75 мужских, а набор для тестов - из 13 женских и 37 мужских. Предложения "sa", общие для всех дикторов, не используются, чтобы избежать возможного отклонения к определенным фонемам. Есть 840 предложений для обучения и 400 предложений для тестирования. Частота дискретизации речевых сигналов составляет 16 кГц.
Для проведения исследования, мы отказались от тихих сегментов /#h/, /h#/,/epi/ и /pau/, так как нас больше интересуют фонемы отличные от тишины. Оставшиеся 59 фонем из фонетического набора TIMIT были использованы при моделировании. Большинство систем распознавания речи [14, 13, 15] для моделирования используют только около 42 - 48 фонем. Это достигнуто путем группировки аллофонов в одну фонемную группу. 15 аллофонов из фонетического набора TIMIT определены в [14]. В итоге, имеется семь групп аллофонов, показанных в Таблице 1, где отклонения в пределах группы не засчитываются за ошибку. Таким образом, 59 фонем определены, но для однозначности, эффективно использовать только 46. В таком случае, коэффициент распознавания фонем представляет собой коэффициент правильного распознавания [15].
Все речевые сигналы предварительно усилены коэффициентом 0.95 до параметризации. Наша основная система использует Mel-частотные кепстральные коэффициенты, которые были вычислены, используя 40 треугольных полосовых фильтров, как описано в [4]. Продолжительность каждого анализируемого окна составляет 20 миллисекунд с наложением в 10 миллисекунд. Кепстральные коэффициенты кратны 12 и представлены в виде векторов.
Распознаватель фонем состоит из 59 фонемных моделей. Каждая фонема смоделирована тремя положениями HМM слева направо. Результирующее распределение вероятности каждого положения смоделировано при помощи комбинации трех многомерных Гауссовых функций плотности с диагональной матрицей ковариации.
Первоначальная оценка HMM параметров найдена при использовании сегментального алгоритма K-средних. Затем используется алгоритм переоценки Baum-Weltch'а, для увеличения первоначальной оценки. Во время процесса переоценки нижнее значение вероятности перехода и смешанных коэффициентов выбрано равным 0.00001, а для диагональных элементов матрицы ковариации равным 0.01.
Аналогичная HMM система использовалась для всех тестов (Mel-scale кепстральные коэффициенты и вейвлет преобразование).
Оконные вейвлеты широко используются при анализе речи. Например, Гаусса (вейвлет Morlet) [12, 11], окно Hamming [2], и окно Hanning [1, 5]. Важно выбрать вейвлет функцию, которая бы подходила для решения поставленной задачи. Например, MHAT вейвлет популярен при анализе зрительных образов, но не подходит для анализа речи из-за его низкой частотной характеристики, которая приводит к низкому разрешению. Мы выбрали вейвлет Morlet, для выполнения SCWT.
После нормализации, выбрав 
, вейвлет Morlet определяется как
Вейвлеты Morlet изображены на рис. 1.
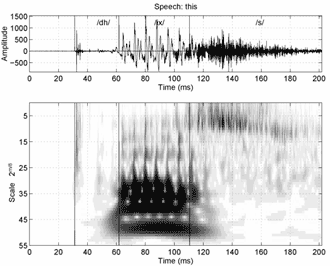
Материнский вейвлет - комплексная функция, и поэтому коэффициенты CWT - комплексные числа. В нашем случае, N0 = 10 и 
. Вейвлет Morlet имеет постоянное значение Q около 3.3087, что соответствует 1/2.28 полосе пропускания октавы. Иллюстрация 2 показывает сегмент речи, обработанный SCWT с a0 = 1, V = 8 и m=0..., 53. b0 равно 1 для всех масштабов. Изображение гармоник и формантов представлены на одном графике. Результат SCWT - сглажен полуволной. Затем снижается от 16 кГц до 100 Гц. Кепстральный анализ используется для уменьшения количества вейвлет коэффициентов до 12 кепстральных, которые используются в дальнейшем в HMM системе для распознавания фонемы.
Наш пример DWT основан на вейвлете Daubechies. Этот вейвлет является одним из самых популярных и используется для распознавания речи [10]. Вейвлет Daubechies 8 порядка показан на рис. 3.
Как уже было отмечено ранее, DWT реализован используя FWT, при этом используется масштаб кратный двум. Часть FWT речевого сигнала, с применением вейвлета Daubechies, изображена на рис. 4. Речь обработана FWT, для получения 6 масштабов, охватывающих 6 октав. Два коэффициента FWT с наибольшими значениями в каждом масштабе, они обновляются каждые 8 миллисекунд, используя неперекрывающиеся окна. Заметьте, что число отсчетов для каждого окна различно при всех масштабах. Поэтому, 12 FWT коэффициентов получены от каждого анализируемого окна. Эти FWT коэффициенты подаются на вход XMM системе. Параметризация FWT отображает большие начальные колебания.
Главное преимущество скалограмм (SCWT) по сравнению со спектрограммами (STFT) состоит в том, что они могут отображать и гармоническую структуру и структуру формантов речевого сигнала, подобный анализ выполняется человеческим ухом. В частности на скалограмме могут быть идентифицированы большие начальные колебания. Ввиду этих особенностей, SCWT, кажется, обладает потенциалом при распознавании речевых фонем.
Результаты распознавания фонем, представленные в данной работе, показывают, что SCWT - существенно лучше, чем DWT для распознавания речи. Однако, усовершенствование SCWT при помощи Mel-scale кепстральных коэффициентов, оказалось очень неэффективным. Это наблюдение может быть уникальным для специфической постобработки, выполняемой с коэффициентам SCWT. В настоящее время проводятся работы для определения так ли это. В частности не ясно, как мелкие особенности скалограммы могут быть использованы при параметризации, для дальнейшего увеличения коэффициента правильного распознавания, в тоже время без значительного увеличения времени вычислений. Итак, отметим, что время вычислений для выполнения SCWT намного больше, чем для DWT, а также для Mel-scale кепстральных коэффициентов.