Есть несколько точек зрения, чтобы расценить то, к чему мы подразумеваем сделанное в этой статье. Главное побуждение является экономическим политическим: мы желаем к последовательно расширить предпочтение по политическим партиям к комитетам (например, парламенты) составленный из их представителей. Мы предполагаем, что любые два участника из той же самой политической партии, сидящей в комитете, преследуют ту же самую политику и, следовательно, неразличимы. Другая интерпретация проблемы расширение полного заказа по "алфавиту" "писем" к свободным коммутативным полугруппам "слов", где заказ писем в слове игнорируемый и продукт любых двух слов - их связь. Действительно, беря любой непустой набор как наш набор политических партий или, соответственно, наш алфавит, мы интересуемся комитетами или, соответственно, слова, которые могут быть сформированы из членов A, и в любом случае мы расцениваем любые два комитета, слова, u и v как эквивалентный, когда, для каждого участник количество раз встревание является тем же самым в u как в v. Данный линейный заказ относительно A, набор комитетов может быть рассмотрен как набор всех не уменьшаемых конечных последовательностей элементов A. Именно в этой форме вопрос последовательного расширения предпочтения на наборе политических партий к набору комитетов был предложен Sertel [1] в ряду лекций, как позже также издано в Sertel и Kalayc?o?glu [2]. Другой набор мотивации заявлений останавливает от факта это, в различной ветви математики и информатики, ранжирования слов построенный из элементов определенного набора A использовались для некоторых время. Набор всех таких слов, обычно называемых "мультимножествами" на A, будет обозначенный как P (A). Понятие мультимножества обобщает понятие множество, так как слово может содержать несколько идентичных элементов A. Математически говоря, мультимножество М. на наборе A является парой М. = (A, µ), где µ: > N функция, от до набора N всех неотрицательных целых чисел, который для каждого элемент Єx A дает разнообразие (число возникновений) µ (a) a. Обычные понятия для множеств могут быть перенесены на мультимножества в естественном виде. Предположим впредь, что A конечен с = {a1...,} для некоторых n ?x N, количество элементов мультимножества М. = (A, µ) может быть определен как сумма (M) = µ (a1) +µ (a2) +... +µ. Мы говорим что мультимножество M1 = (A, µ1) подмножество мультимножества M2 = (A, µ2) и писать M1 Сz M2 если µ1 (a) ? µ2 (a) для всего Єx A. Ранжирование P (A) и его подмножества, которые расширяют данное ранжирование из A способствовали доказательствам завершения программы, рассуждающие алгоритмы, основанные на системах переписывания срока, по компьютерной алгебре, теория инвариантов, и теория разделения. Возвращаясь к экономическим побуждениям, мы отмечаем что результат лотереи играемый несколько раз мультимножество призов. И хотя это может быть обсужденный, что "реальное" предпочтение по результатам и не лотереям, von Neumann и Morgenstern [5] избегали трудности сравнения мультимножества из призов, определяя предпочтение по лотереям непосредственно. Однако практичные наблюдения показали так называемые “парадоксы сервисной теории”, которые показывают что von Neumann и теория Morgenstern не может объяснить определенный экспериментальные результаты [6, 7]. В этом отношении интересно заняться расследованиями что вид из предпочтения могли бы люди иметь на наборе всех мультимножеств призов и есть ли у всего этого предпочтения так называемая “ожидаемая полезность”, структура. Другой стимул рассмотреть расширения ранжирования от до P (A)
и его подмножества - то, что это могло бы служить общей основой объединения к a число тем в экономической литературе, которая может иначе появиться как несвязанный. С одной стороны у нас есть экстенсивно изученная тема ранжирования подмножества A, учитывая ранжирование на A. Читатель отнесен для литературы на этой теме к обзору Barber.a, Bossert и Pattanaik [8]. Но другая сторона - многие источники в теории представления измерения, главным образом Fishburn [9, 10, 12] при ранжировании конечного Последователя Декарта продукты A1. A2...... могут интерпретироваться в терминах ранжирования из мультимножеств, но связи между ранжированием Декартовских продуктов и ранжирование мультимножеств нуждается в дальнейшем исследовании. Следующий [8], любое рефлексивное, полное и переходное отношение назовут заказ и любой антисимметрический заказ назовут линейным заказом. Заказы на P (A) будет типично обозначаться как _. В этом случае _ будет строгое привилегированное отношение _, то есть. М. _ Nбудет означать, что М. _ Nдержится, но N_ М. терпит неудачу, и М. ?Nбудет отношением безразличия _, то есть. М. ?Nбудет означать, что и М. _ Nи N_ М. держится. Заказы следующего типа играют исключительную роль в статистике [13, 14], представительная теория измерения и принятия решения [10], также как информатика [11] и связанные другие области.
Определение 1. Позвольте Pбыть семьей мультинаборов на A. Заказ _ на Pсказан чтобы быть совокупно перепрезентабельными (или просто добавка) iff там существуют неотрицательные действительные числа w1..., wmтаким образом, что, для всего М. = (A, µ), N= (A, ?) принадлежность к P,
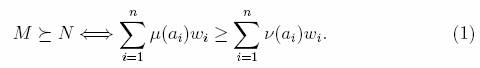
Knuth и Bendix [11] заменяя каждый срок мультинабором, состоящим из функциональных символов, происходящих в этом сроке и тогда назначая веса на каждый функциональный символ. Они тогда вычисляли общая масса каждого срока и оцениваемый сроки соответственно. Такая добавка заказ термина алгебра теперь известен как заказ Knuth-Bendix. Мы также обратимся к числам w1..., wn как веса a1.... В литературе эти числа часто упоминаются "как утилиты" или, когда w1 + w2 +... + wn = 1, интуитивные вероятности [13, 14]. Когда мы устанавливаем веса тогда мы естественно определяем заказ не только на A но также и его расширении к заказу P (A). Подобное понятие совокупной перепредставительности было также определено для заказов на Декартовском продукте A1. A2...... Здесь полезность кортежа a = (a1, a2...,), определен как u (a) = u1 (a1) +u2 (a2) +... +un, где ui - сервисная функция для Ай. Есть обширная литература по очевидной характеристике добавки заказы. Условие, представленное ниже на Определении 2, было предложено de Finetti [13] и игры центральная роль в этой литературе. Сформулировать это мы должны определить операцию союза мультинабора. К этому концу, учитывая любого два мультинабора M1 = (A, µ1) и M2 = (A, µ2) на A, их союзом M1 ?~M2 мы подразумеваем мультинабор (A, µ), для который µ (a) = µ1 (a) + µ2 (a) для всего ?xA. Мы отмечаем, что союз определил, таким образом соответствует продукту мультинаборы, рассматриваемые как элементы свободной полугруппы на A.
Определение 2. Позвольте P быть семьей мультинаборов на A. Мы говорим что заказ _ на P сохранен при операции союза мультинабора iff, для любого U, V и W, принадлежащий P с U ?~W и V ?~W также в P, мы имеем всякий раз, когда U?~Wи V?~Wоба определены, то есть они - также элементы от P.
![]()
Сила этого условия может измениться в зависимости от структуры P под частичным порядком включения мультинаборов. Действительно, если P - ряд всех мультинаборы неподвижного количества элементов, тогда никакие два подмножества Uи Vпринадлежностей Pимейте их союз снова в P, и это условие не ограничивает заказы относительно Pвообще. С другой стороны, если Pсодержит все подмножества единичного предмета A, то это условие довольно сильно. De Finetti и многие другие исследователи исследовали заказы относительно набор P= 2Aвсех подмножеств конечного набора A. Для подмножеств мультинабор союз двух наборов - обычный теоретический набором союз, если наборы являются несвязными и это не определено иначе. Это был de Finetti, который заметил это для прикажите _ на наборе P= 2Aбыть совокупными, это необходимо что этот заказ сохранен при операции союза мультинабора. С другой стороны, Крафт - бумага и другие [15] построила заказ относительно подмножеств набора строение из пять элементов, который сохранен при операции союза мультинабора, но однако, недобавка. (Крафт - бумага и другие [15] упомянула сохраненные заказы при операции союза мультинабора как "добавка" (со значением весьма отличный от нашего значения для этого срока). Это условие также назвали “сильная расширенная независимость” в [8]. В литературе информатики, этой собственности заказа относительно семьи из мультинаборов назван "скучностью". Это гарантирует, что есть не бесконечно уменьшение цепей мультинаборов, который полезен в доказательстве завершения программы [4]. Интерес этой собственности уменьшился значительно с тех пор Мартин [3] показал что когда P= P (A), то есть. P- семья всех мультинаборов, все заказы, сохраненные при операции союза мультинабора, являются совокупными (то есть Заказы Knuth-Bendix). Поэтому для этих двух естественных выборов P– когда P- набор всех подмножеств и когда P- набор всех мультинаборов - мы добираемся два различных результата. Причина то, что в последнем случае операция союз мультинабора всегда определяется, делая более сильное условие. Во многих целях Определение 2 является слишком ограничительным. Действительно, предположите это мы можем назначить полезность wiна каждый элемент ай ?xA. Это определит a определенный заказ относительно A. Тогда, для любого мультинабора М. = (A, µ) позволяют нам говорить что единое время ценности (M) = _ni=1 µ (ай) wiпредставляет “полное совершенство” М. Если мы оцените мультинаборы в соответствии с их полным совершенством, тогда мы получаем заказ (1) который сохранен при операции союза мультинабора. Но если мы определяем ценность
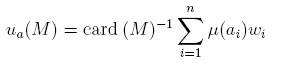
представление “среднего совершенства” М. и заказа мультиустанавливает соответственно, то есть.
![]()
тогда этот заказ не будет удовлетворять условие (2), хотя это соглашается с заказ относительно решительного утилитами и расширяет этот заказ на P (A) в некоторый естественный путь. Этот вид расширения заказа относительно к заказу относительно P (A) может быть полезным в некоторых заявлениях. В продолжении мы будем часто идентифицировать элементы Aи передачи подмножества единичного предмета A.
Определение 3. Позвольте быть заказанным набором и Pбыть семьей мультинаборов на Aкоторый содержит все подмножества единичного предмета. Заказ _ на P, как говорят, слабо последовательное расширение данного заказа относительно iff, 1. Заказ, вызванный _ на подмножествах единичного предмета, совпадает с линейным заказ относительно A; 2. для любых двух мультинаборов U, Vиз равного количества элементов и любой принадлежности Wк P,
![]()
всякий раз, когда U?~Wи V?~Wоба принадлежат P.
Теперь, ли мы определяем заказ относительно мультинаборов на основе полного совершенства или среднее совершенство, оба заказа мультинаборов удовлетворят слабую последовательность. Что мы можем ожидать из слабо последовательных заказов? Конечно, мы не можем ожидайте, что они все будут совокупными, как показы заказа (3). Но что мы можем все еще надежда на - то, что следующая собственность слабой аддитивности держится.
Определение 4. Позвольте P?zP (A). Заказ _ на P, как говорят, является слабо совокупным iff там существуют неотрицательные действительные числа w1..., wnтаким образом, что, для любых двух мультинаборы М. = (A, µ), N= (A, ?) того же самого количества элементов, принадлежащего P, нам иметь
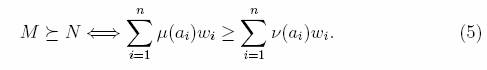
Важно подчеркнуть, что веса имели обыкновение определять слабо совокупный заказ не предоставляет нам любое основание, чтобы сравнить мультинаборы различные количества элементов. В этой газете мы предпринимаем исследование заказов трех критических наборов из мультинаборов. Учитывая набор оборудованный линейным заказом _, сначала мы будем заинтересуйтесь расширением _ к слабо последовательным заказам набора P (A) всех мультинаборов, и к таким заказам набора P ?k (A) всех мультинаборов из количества элементов ? k. Мы также заинтересуемся распространением _ к набору Pk (A) всех мультинаборов количества элементов k. Например, если мы хотим сравниться два состава парламента мы должны сравнить мультинаборы неподвижного количество элементов. Ниже мы обсуждаем то, чем это означает для заказа относительно Pk (A) быть совместимый с данным заказом относительно A.
Определение 5. Мы говорим, что заказ _ на Pk (A) последователен (с данным заказ относительно A) iff там существует слабо последовательный заказ относительно P ?k (A), который совпадает с _ на мультинаборах количества элементов k.
Альтернативно мы могли определить последовательный заказ относительно Pk (A) рекурсивно следующие условия:
1. Данный заказ относительно A вызывает единственный последовательный заказ относительно P1 (A);
2. Позвольте _ быть заказом относительно Pk (A), k ? 2, и позволять 1 ? j <k. Тогда для любого W ?x Pj (A) мы можем определить заказ _W относительно Pk?j (A), устанавливая, для любого U, V ?x Pk?j (A),
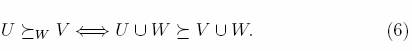
предусматривает, поскольку я =2..., k?1, существование последовательных заказов относительно Пи (A), удовлетворяя (6). Это конечно, эквивалентно существованию слабо последовательного заказа относительно P ?k (A), который совпадает с _ на Pk (A). Это условие последовательности более сильно чем аналог Bossert’s условие живого отклика [16], который он изучил для заказов подмножеств неподвижных количество элементов, но он также принимал очень сильное условие нейтралитета который мы не принимайте здесь. Позвольте нам теперь анонсировать наши результаты в этой газете. Без потери общности, мы предполагаем что набор = [n] = {1, 2..., n} и это Мы предполагаем, что заказ относительно (или относительно его подмножеств единичного предмета) линеен с тех пор случай, когда {я} ? {j} для некоторых я и jне интересны и можем быть легко уменьшенный до (7) для меньшего n. Чтобы упростить примечание, мы идентифицируем {я} с я и сокращаю P ([n]), P ?k ([n]) и Pk ([n]) к P [n], P ?k [n] и Pk [n], соответственно. Мы также опустим [n], когда это не пригласит беспорядка. Мы доказываем что, для набора с 3 элементами = [3], для всех целых чисел k? 1, все слабо последовательные заказы относительно P ?k [3] являются слабо совокупными и следовательно все последовательный заказы относительно Pk [3] являются совокупными для всего k. Мы классифицируем совокупные заказы относительно Pk [3] посредством фракций Farey и находят свой asymptotics. Когда = [4], мы показываем, что там существуют 12 последовательных линейных заказов относительно P2 [4], что два из их, а именно, A4 и E4 в иллюстрации 1, являются несовокупными. Кроме того, нет слабо последовательный линейный заказ относительно P ?2 [4] совпадение с A4 или E4 на мультинаборах количество элементов 2 может быть расширено на слабо последовательный заказ относительно P ?3 [4]. Мы доказываем, что там существует, положительное целое число оценило функцию k_ > f (k) таким образом, что, для n? 4, линейный заказ _ на P ?k [n] может быть расширен на слабо последовательный линейный заказ P ?f (k) [n] iff _ является слабо совокупным на P ?k [n]. Как заключение, любой слабо последовательный линейный заказ относительно P [n] является слабо совокупным, если нас с аналогом результата из-за Мартина [3]. Наконец, для произвольного положительного целого числа n, мы даем более низкое направляющееся в число совокупных линейных заказов относительно P2 [n] и более низкого направляющегося в общее количество последовательных линейных заказов относительно P2 [n].
Полный текст статьи а английском языке: http://www.nyu.edu/sed2002/pdfs/vdm1-1-txt.pdf
Литература
- Sertel,M.R.: “Oral Communication,” 1990.
- Sertel,M.R. and Kalayc©ҐoўЁglu,E.: Toward the Design of a New Electoral
Method for Turkey (in Turkish), TЎ§USIAD, Istanbul, 1995. - Martin,U.: “A Geometric Approach to Multiset Ordering,” Theoretical
Computer Science, 67 (1989), 37–54. - Dershowitz,N.: “Termination of Rewriting.” In: Proc. First Internat.
Conf. on Rewriting Techniques and Applications, Lecture Notes in Computer
Science, Vol 202 (Springer, Berlin, 1985), 180–224. - Von Neumann, J. and Morgenstern, O. Theory of Games and Economic
Behavior. Princeton University Press, Princeton, 1944. - Allais,M. and Hagen,O. eds.: Expected Utility Hypotheses and Allais
paradox. Dordrecht, Holland: Reidel, 1979. - Machina,M.J.: “Generalized expected utility analysis and the nature
of observed violations of the independence axiom.” In: Stigum,B. and
Wenstop,F. (eds.), Foundations of Utility and Risk Theory with Applications,
Dordrecht, Holland: Reidel, 1983. - Barber.a,S., Bossert,W. and Pattanaik,P.K.: “Ordering Sets of Objects.”
In: Salvador Barber, Peter J. Hammond and Christian Seidl (eds.),
Handbook of Utility Theory. Volume 2, Chapter 17. Kluwer Academic
Publishers, Dordrecht-Boston, 2001. - Fishburn,P.C.: Utility Theory for Decision Making. New York: John
Wiley and Sons, 1970. - Fishburn,P.C.: “Finite Linear Qualitative Probability,” Journal of
Mathematical Psychology, 40 (1996), 64–77. - Knuth,D.E., and Bendix,P.B.: “Simple word problems in universal algebras.”
In: Leech,J. (ed.), Computational Problems in Abstract Algebra,
Oxford: Pergamon, 1970, 263–297. - Fishburn,P.C.: “Failure of Cancellation Conditions for Additive Linear
Orders,” Journal of Combinatorial Design, 5 (1997), 353–365. - de Finnetti,B.: “Sul significato soggetivo della probabilit`a,” Fundamenta
Mathematicae, 17 (1931), 298–329. - Savage,L.J.: The Foundations of Statistics. New York: John Wiley and
Sons, 1954. - Kraft,C.H., Pratt,J.W., and Seidenberg,A.: “Intuitive Probability on
Finite Sets,” Annals of Mathematical Statistics 30 (1959), 408–419. - Bossert,W.: “Preference Extension Rules for Ranking Sets of Alternatives
with a Fixed Cardinality,” Theory and Decision, 39 (1995), 301–
317. - Hardy, G.H., and Wright,E.M.: An Introduction to the Theory of Numbers.
Oxford, 1960. - Dickson,L.E.: History of the Theory of Numbers. Chelsea, New York,
1971. - Chandrasekharan,K. Introduction to Analytic Number Theory. Springer-
Verlag, New York, 1968. - Hadamard,J.: “R.esolution d’une question relative aux d.eterminants,”
Bull. Sci. Math., (2) 17 (1893), 240–248. - Zhevlakov,K.A., Shestakov,I.P., Shirshov,A.I., Slinko,A.M. Rings that
are nearly associative. Academic Press, New York - London, 1982. - Peng,I. Private communication.
- Gardner,M. “Catalan Numbers.” In: Time Travel and Other Mathematical
Bewilderments, New York: W.H.Freeman, 1988, pp. 253–266. - Vardi,I. Computational recreations in Mathematica. Redwood City, California:
Addison-Wesley, 1991.