There are several viewpoints from which to regard what we purport to do in this paper. The main motivation is politico-economic: we wish to con- sistently extend preferences over political parties to committees (e.g., parlia- ments) composed of their representatives. We assume that any two members of the same political party sitting on a committee pursue the same policy and are, hence, indistinguishable. Another interpretation of the problem is the extension of a total order over an “alphabet” of “letters” to the free commutative semigroup of “words,” where the order of letters in the word is disregarded and the product of any two words is their concatenation.
Indeed, taking any non-empty set A as our set of political parties or, re- spectively, our alphabet, we are interested in the committees or, respectively, the words which can be formed of members of A, and in any case we regard any two committees, or resp., words, u and v as equivalent when, for each member a of A the number of times a occurs is the same in u as in v. Given a linear order on A, the set of committees can be viewed as the set of all non-decreasing ?nite sequences of elements of A. It is in this form that the question of the consistent extension of preferences on the set of political par- ties to the set of committees was proposed by Sertel [1] in a series of lectures, as later also published in Sertel and Kalayc?og?lu [2].
Another set of motivating applications stems from the fact that, in dif-
ferent branches of mathematics and computer science, rankings of words
constructed of elements of a certain set A have been in use for quite some
time. The set of all such words, commonly called “multisets” on A, will be denoted as P (A). The concept of a multiset generalizes the concept of a set, since a word may contain several identical elements of A. Mathematically speaking, a multiset M on a set A is a pair M = (A, µ), where µ: A > N is
a function, from A to the set N of all nonnegative integers, which for each element a ? A gives the multiplicity (the number of occurrences) µ(a) of a. The usual notions for sets can be carried over to multisets in a natural way. Assuming henceforth that A is ?nite with A = {a1 ,... , an} for some n ? N, the cardinality of a multiset M = (A, µ) can be de?ned as the sum card (M ) = µ(a1)+ µ(a2)+ ... + µ(an). We say that a multiset M1 = (A, µ1) is a subset of a multiset M2 = (A, µ2) and write M1 ? M2 if µ1(a) ? µ2 (a) for all a ? A. Rankings of P(A) and its subsets which extend a given ranking of A have been instrumental in proofs of program termination, in equational reasoning algorithms based on term rewriting systems, in computer algebra, the theory of invariants, and the theory of partitions. We refer the reader to the two surveys by Martin [3] and Dershowitz [4] on these topics.
Returning to economic motivations, we note that the outcome of a lot- tery played several times is a multiset of prizes. And although it can be argued that the “real” preferences are over outcomes and not lotteries, von Neumann and Morgenstern [5] avoided the di?culty of comparing multisets of prizes by de?ning preferences over lotteries directly. Nevertheless practical observations revealed the so-called “paradoxes of utility theory,” which show that von Neumann and Morgenstern theory cannot explain certain experi- mental results [6, 7]. In this respect it is interesting to investigate what kind of preferences might individuals have on the set of all multisets of prizes and whether all these preferences have the so-called “expected utility” structure.
Another incentive to consider extensions of rankings from A to P (A)
and its subsets is that it might provide a common unifying framework to a
number of topics in the economics literature which may otherwise appear as
unrelated. On the one hand we have an extensively studied topic of ranking
subsets of A, given a ranking on A. The reader is referred for the literature
on this topic to the survey by Barbera?, Bossert and Pattanaik [8]. On the
other hand there are a number of papers in the representation theory of
measurements, mostly by Fishburn [9, 10, 12] on ranking ?nite Cartesian products A1 ? A2 ? ... ? An. Both can be interpreted in terms of rankings of multisets but the connection between rankings of Cartesian products and rankings of multisets needs further investigation.
Following [8], any re?exive, complete and transitive relation will be called an order and any antisymmetric order will be called a linear order. Orders on P (A) will typically be denoted as . In this case will be the strict preference relation of , i.e. M N will mean that M N holds but N M fails, and M ? N will be the indi?erence relation of , i.e. M ? N
will mean that both M N and N M hold.
Orders of the following type play an exceptional role in statistics [13, 14],
the representational theory of measurement and decision making [10], as well
as computer science [11] and related other areas.
De?nition 1. Let P be a family of multisets on A. An order on P is said to be additively representable (or simply additive) i? there exist nonnegative real numbers w1 ,... , wm such that, for all M = (A, µ), N = (A, ?) belonging to P,
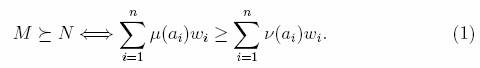
Knuth and Bendix [11] ordered the term algebra by replacing every term by the multiset consisting of functional symbols occurring in this term and then assigning weights to each functional symbol. They then calculated the total weight of every term and ranked the terms accordingly. Such an additive order of the term algebra is now known as a Knuth-Bendix order.
We will also refer to the numbers w1,... , wn as the weights of a1 ,... , an. In the literature these numbers are often referred to as “utilities” or, when w1 + w2 + ... + wn = 1, intuitive probabilities [13, 14]. When we ?x weights then we naturally determine an order not only on A but also its extension to an order of P (A).
A similar concept of additive representability was also de?ned for orders
on a Cartesian product A1 ? A2 ? ... ? An. Here the utility of the tuple
a = (a1 , a2,... , an) is de?ned as u(a) = u1(a1 )+ u2(a2 )+ ... + un(an), where
ui is a utility function for Ai.
There is an extensive literature on the axiomatic characterization of ad-
ditive orders. The condition presented below in De?nition 2 was suggested
by de Finetti [13] and plays a central role in this literature. To formulate it
we need to de?ne the operation of multiset union. To this end, given any
two multisets M1 = (A, µ1) and M2 = (A, µ2) on A, by their union M1 ? M2 we mean the multiset (A, µ), for which µ(a) = µ1 (a) + µ2(a) for all a ? A. We note that the union de?ned in this way corresponds to the product of multisets viewed as elements of the free semigroup on A.
De?nition 2. Let P be a family of multisets on A. We say that an order
on P is preserved under the operation of multiset union i?, for any U, V
and W belonging to P with U ? W and V ? W also in P, we have
![]()
whenever U ? W and V ? W are both de?ned, i.e. they are also elements from P .
The strength of this condition can vary depending on the structure of P under the partial order of inclusion of multisets. Indeed, if P is a set of all multisets of ?xed cardinality, then no two subsets U and V belonging to P have their union again in P and this condition does not restrict orders on P at all. On the other hand, if P contains all singleton subsets of A, then this condition is rather strong.
De Finetti and a number of other researchers investigated orders on the set P = 2A of all subsets of a ?nite set A. For subsets of A the multiset union of two sets is an ordinary set-theoretic union if the sets are disjoint and it is not de?ned otherwise. It was de Finetti who noticed that for an order on the set P = 2A to be additive it is necessary that this order is preserved under the operation of multiset union. On the other hand, Kraft et al [15] constructed an order on subsets of a set A consisting of ?ve elements which is preserved under the operation of multiset union but is, nevertheless, non-additive. (Kraft et al [15] referred to orders preserved under the operation of multiset union as “additive” (with a meaning quite distinct from our meaning for this term). This condition was also called “strong extended independence” in [8].
In the computer science literature, this property of an order on a family of multisets is called “tameness.” It guarantees that there are no in?nitely decreasing chains of multisets, which is helpful in proving program termi- nation [4]. The interest of this property has decreased signi?cantly since Martin [3] showed that when P = P (A), i.e. P is the family of all multisets, all orders preserved under the operation of multiset union are additive (i.e. Knuth-Bendix orders). Therefore for these two natural choices of P - when P is the set of all subsets and when P is the set of all multisets - we get two di?erent results. The reason is that in the latter case the operation of multiset union is always de?ned, making the condition stronger.
For many purposes De?nition 2 is too restrictive. Indeed, suppose that we can assign a utility wi to each element ai ? A. This will determine a certain order on A. Then, for any multiset M = (A, µ) let us say that the i=1 value ut(M ) = nµ(ai)wi represents the “total goodness” of M . If we rank multisets in accordance with their total goodness, then we get the order
(1) which is preserved under the operation of multiset union. But if we de?ne
the value
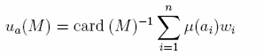
representing the “average goodness” of M and order multisets accordingly, i.e.
![]()
then this order will not satisfy the condition (2) although it agrees with the order on A determined by the utilities and extends this order to P(A) in some natural way. This kind of extension of an order on A to an order on P(A) can be useful in some applications.
In the sequel, we will often identify elements of A and the corresponding
singleton subsets of A.
De?nition 3. Let A be an ordered set and P be a family of multisets on A which contains all singleton subsets. An order on P is said to be a weakly consistent extension of the given order on A i?,
1. The order induced by on singleton subsets coincides with the linear order on A;
![]() 2. for any two multisets U, V of equal cardinality and any W belonging to P,
2. for any two multisets U, V of equal cardinality and any W belonging to P,
![]()
whenever U ? W and V ? W both belong to P.
Now, whether we de?ne an order on multisets on the basis of total good- ness or average goodness, both orders of multisets will satisfy weak consis- tency.
What can we expect from weakly consistent orders? Of course, we cannot expect them all to be additive, as the order (3) shows. But what we can still hope for is that the following property of weak additivity holds.
![]() De?nition 4. Let P? P(A). An order on P is said to be weakly additive i? there exist nonnegative real numbers w1,... , wn such that, for any two multisets M = (A, µ), N = (A, ?) of the same cardinality belonging to P, we have
De?nition 4. Let P? P(A). An order on P is said to be weakly additive i? there exist nonnegative real numbers w1,... , wn such that, for any two multisets M = (A, µ), N = (A, ?) of the same cardinality belonging to P, we have
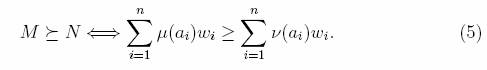
It is important to emphasize that the weights used to determine a weakly additive order do not provide us with any basis to compare multisets of di?erent cardinalities.
In this paper we undertake an investigation of orders of three critical sets of multisets. Given the set A equipped with a linear order , ?rst we will be interested in the extension of to weakly consistent orders of the set P(A) of all multisets, and to such orders of the set P?k(A) of all multisets of cardinality ? k. We will also be interested in extending to the set Pk(A) of all multisets of cardinality k. For example, if we want to compare two compositions of a parliament we need to compare multisets of a ?xed cardinality. Below we discuss what it means for an order on Pk(A) to be consistent with a given order on A.
De?nition 5. We say that an order on Pk(A) is consistent (with a given order on A) i?there exists a weakly consistent order on P?k(A) which coin- cides with on the multisets of cardinality k.
Alternatively we could de?ne a consistent order on P k (A) recursively by the following conditions:
1. The given order on A induces the only consistent order on P1 (A);
2. Let be an order on P k (A), k ? 2, and let 1 ? j< k. Then for any W ? P j(A) we may de?ne an order W on Pk?j(A) by setting, for any U, V ? P k?j(A),
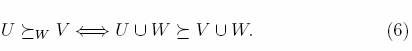
An order of Pk(A), k ? 2, is said to be consistent i? for every j = 1, 2,... ,k ? 1, the orders W for all W ’s of ?xed cardinality j coincide and this common order is a consistent order of P k?j(A).
In other words, any consistent order of Pk(A) stipulates, for i =
2,... ,k ?1, the existence of consistent orders on P i(A), satisfying (6). This
is, of course, equivalent to the existence of a weakly consistent order on
P?k(A) which coincides with on Pk(A).
This condition of consistency is stronger than the analogue of Bossert’s condition of responsiveness [16], which he studied for orders of subsets of ?xed
cardinality, but he also assumed a very strong neutrality condition which we do not assume here.
Let us now preview our results in this paper. Without loss of generality, we assume that the set A = [n] = {1,2,... , n} and that
We assume that the order on A (or on its singleton subsets) is linear since
the case when {i}?{j} for some i and j is not interesting and can be easily reduced to (7) for smaller n. To simplify notation we will identify {i} with i and abbreviate P ([n]), P?k([n]) and P k ([n]) to P[n], P?k[n] and Pk[n], respectively. We will also omit [n] when this invites no confusion.
We prove that, for a 3-element set A = [3], for all integers k ? 1, all weakly consistent orders on P?k[3] are weakly additive and hence all con- sistent orders on Pk[3] are additive for all k. We classify additive orders on Pk[3] by means of Farey fractions and ?nd their asymptotics. When A = [4], we show that there exist 12 consistent linear orders on P2[4], that two of them, namely A4 and E4 in Figure 1, are non-additive. Moreover, no weakly consistent linear order on P ?2[4] coinciding with A4 or E4 on multisets of cardinality 2 can be extended to a weakly consistent order on P?3 [4].
We prove that there exists a positive integer valued function k > f(k) such that, for n ? 4, a linear order on P?k[n] can be extended to a weakly consistent linear order of P ?f(k)[n] i? is weakly additive on P?k[n]. As a corollary, any weakly consistent linear order on P [n] is weakly additive,
providing us with the analogue of a result due to Martin [3].
Finally, for an arbitrary positive integer n, we give the lower bound for the number of additive linear orders on P 2[n] and the lower bound for the total number of consistent linear orders on P 2[n].
Čńňî÷íčę: http://www.nyu.edu/sed2002/pdfs/vdm1-1-txt.pdf
Ëčňĺđŕňóđŕ
- Sertel,M.R.: “Oral Communication,” 1990.
- Sertel,M.R. and Kalayc©Ąo˘¨glu,E.: Toward the Design of a New Electoral
Method for Turkey (in Turkish), Tˇ§USIAD, Istanbul, 1995. - Martin,U.: “A Geometric Approach to Multiset Ordering,” Theoretical
Computer Science, 67 (1989), 37–54. - Dershowitz,N.: “Termination of Rewriting.” In: Proc. First Internat.
Conf. on Rewriting Techniques and Applications, Lecture Notes in Computer
Science, Vol 202 (Springer, Berlin, 1985), 180–224. - Von Neumann, J. and Morgenstern, O. Theory of Games and Economic
Behavior. Princeton University Press, Princeton, 1944. - Allais,M. and Hagen,O. eds.: Expected Utility Hypotheses and Allais
paradox. Dordrecht, Holland: Reidel, 1979. - Machina,M.J.: “Generalized expected utility analysis and the nature
of observed violations of the independence axiom.” In: Stigum,B. and
Wenstop,F. (eds.), Foundations of Utility and Risk Theory with Applications,
Dordrecht, Holland: Reidel, 1983. - Barber.a,S., Bossert,W. and Pattanaik,P.K.: “Ordering Sets of Objects.”
In: Salvador Barber, Peter J. Hammond and Christian Seidl (eds.),
Handbook of Utility Theory. Volume 2, Chapter 17. Kluwer Academic
Publishers, Dordrecht-Boston, 2001. - Fishburn,P.C.: Utility Theory for Decision Making. New York: John
Wiley and Sons, 1970. - Fishburn,P.C.: “Finite Linear Qualitative Probability,” Journal of
Mathematical Psychology, 40 (1996), 64–77. - Knuth,D.E., and Bendix,P.B.: “Simple word problems in universal algebras.”
In: Leech,J. (ed.), Computational Problems in Abstract Algebra,
Oxford: Pergamon, 1970, 263–297. - Fishburn,P.C.: “Failure of Cancellation Conditions for Additive Linear
Orders,” Journal of Combinatorial Design, 5 (1997), 353–365. - de Finnetti,B.: “Sul significato soggetivo della probabilit`a,” Fundamenta
Mathematicae, 17 (1931), 298–329. - Savage,L.J.: The Foundations of Statistics. New York: John Wiley and
Sons, 1954. - Kraft,C.H., Pratt,J.W., and Seidenberg,A.: “Intuitive Probability on
Finite Sets,” Annals of Mathematical Statistics 30 (1959), 408–419. - Bossert,W.: “Preference Extension Rules for Ranking Sets of Alternatives
with a Fixed Cardinality,” Theory and Decision, 39 (1995), 301–
317. - Hardy, G.H., and Wright,E.M.: An Introduction to the Theory of Numbers.
Oxford, 1960. - Dickson,L.E.: History of the Theory of Numbers. Chelsea, New York,
1971. - Chandrasekharan,K. Introduction to Analytic Number Theory. Springer-
Verlag, New York, 1968. - Hadamard,J.: “R.esolution d’une question relative aux d.eterminants,”
Bull. Sci. Math., (2) 17 (1893), 240–248. - Zhevlakov,K.A., Shestakov,I.P., Shirshov,A.I., Slinko,A.M. Rings that
are nearly associative. Academic Press, New York - London, 1982. - Peng,I. Private communication.
- Gardner,M. “Catalan Numbers.” In: Time Travel and Other Mathematical
Bewilderments, New York: W.H.Freeman, 1988, pp. 253–266. - Vardi,I. Computational recreations in Mathematica. Redwood City, California:
Addison-Wesley, 1991.