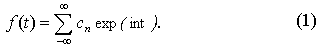
Источник: http://www.krsu.edu.kg/vestnik/2002/v2/a15.html
ВЕЙВЛЕТ-ПРЕОБРАЗОВАНИЕ И АНАЛИЗ ВРЕМЕННЫХ РЯДОВ
П.В. Козлов - канд. физ.-мат. наук Б.Б. Чен - докт. физ.-мат. наук
Wavelet-analysis - a new method for time lines analysis is examined. Review of major mathematical ideas and outputs of wavelet-transformations is given. Some specific applications to the apparatus are shown.
Традиционно для анализа временных рядов используется преобразование Фурье, дающее разложение исследуемого временного процесса f(t) в ряд по тригонометрическим функциям, или в более общей форме записи
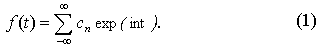
Коэффициенты сn являются амплитудами гармонических колебаний соответствующей частоты и определяются формулой
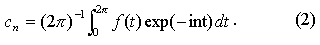
Множество функций exp(int) образует ортонормированный базис пространства L2(0,2p).
Аппарат Фурье-преобразований дает достаточно простые для расчетов формулы и прозрачную интерпретацию результатов, но не лишен и некоторых недостатков. Преобразование, например, не отличает сигнал, являющийся суммой двух синусоид, от ситуации последовательного включения синусоид, не дает информации о преимущественном распределении частот во времени, может дать неверные результаты для сигналов с участками резкого изменения. Исследуемые ряды также далеко не всегда удовлетворяют требованию периодичности и более того, как правило, заданы на ограниченном отрезке времени.
Основы вейвлет-анализа были разработаны в середине 80-х годов Гроссманом и Морле как альтернатива преобразованию Фурье для исследования временных (пространственных) рядов с выраженной неоднородностью. В отличие от преобразования Фурье, локализующего частоты, но не дающего временного разрешения процесса, и от аппарата d-функций, локализующего моменты времени, но не имеющего частотного разрешения, вейвлет-преобразование, обладающее самонастраивающимся подвижным частотно-временным окном, одинаково хорошо выявляет как низко-частотные, так и высокочастотные характеристики сигнала на разных временных масштабах. По этой причине вейвлет-анализ часто сравнивают с "математическим микроскопом", вскрывающим внутреннюю структуру существенно неоднородных объектов.
Указанная универсальность обеспечила вейвлет-анализу широкое использование в самых различных областях знаний. Семейства анализирующих функций, называемых вейвлетами, применяются при анализе изображений различной природы, для изучения структуры турбулентных полей, для сжатия больших объемов информации, в задачах распознавания образов, при обработке и синтезе сигналов, например, речевых, для определения характеристик фрактальных объектов.
Подобно тому, как в основе аппарата преобразований Фурье лежит единственная функция w(t)=exp(it), порождающая ортонормированный базис пространства L2(0,2p) путем масштабного преобразования, так и вейвлет-преобразование строится на основе единственной базисной функции y(t), имеющей солитоноподобный характер и принадлежащей пространству L2(R), т.е. всей числовой оси.
В западной литературе за этой функцией закрепилось название "вейвлет", что означает "маленькая волна", в отечественной иногда ее называют "всплеском", отражая в этом названии и локализацию, и осцилляционный характер поведения.
При конструировании базисной анализирующей функции y(t) должны выполняться следующие необходимые условия.
Локализация - вейвлет должен быть локализован вблизи нуля аргумента как во временном, так и в частотном пространстве.
Нулевое среднее:
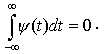
Как следствие, вейвлет должен быть знакопеременной функцией.
Ограниченность:
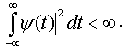
Вейвлет должен быть достаточно быстро убывающей функцией временной (пространственной) переменной.
Базис одномерного дискретного вейвлет-преобразования (ДВП) строится на основе вейвлета y(t) посредством операций сдвигов и растяжений вдоль оси t.
Вводя аналог синусоидальной частоты и принимая для простоты в качестве ее значений степени двойки, получаем для функций базиса Yjk(t)= 2^(j/2)y(2^(j)t-k)
Базис нормирован, если вейвлет имеет единичную норму.
Вейвлет называется ортогональным, если семейство {Yjk} представляет ортонормированный базис функционального пространства L^2(R), т.е.
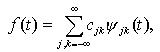
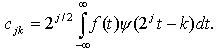
Непрерывное вейвлет-преобразование (НВП) строится аналогичным образом с помощью непрерывных масштабных преобразований и переносов вейвлета y(t) с произвольными значениями масштабного коэффициента a и параметра сдвига b:
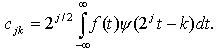
где символ * обозначает операцию комплексного сопряжения.
Вейвлет-преобразование обратимо для функций f из L2(R)
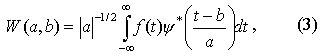
Таким образом, любая функция из L^2(R) может быть представлена суперпозицией масштабных преобразований и сдвигов базисного вейвлета с коэффициентами, зависящими от масштаба (частоты) и параметра сдвига (времени).
Двухпараметрическая функция W(a,b) дает информацию об изменении относительного вклада компонент разного масштаба во времени и называется спектром коэффициентов вейвлет-преобразования.
Располагая вейвлет-спектром, можно рассчитать полную энергию сигнала
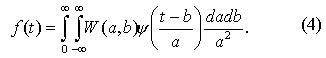
и глобальный спектр энергии - распределение полной энергии по масштабам (скейлограмму вейвлет-преобразования)
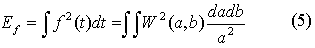
Скейлограмма соответствует спектру мощности Фурье-преобразования сигнала, сглаженному на каждом масштабе спектром Фурье анализирующего вейвлета:
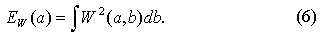
Примеры часто используемых вейвлетов
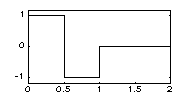
| HAAR - вейвлет: | |||
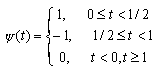 |
 |
||
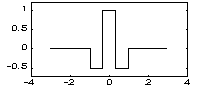
| FHAT - вейвлет ("Французская шляпа" - French hat): | |||
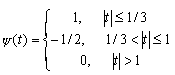 |
 |
||
| Wave - вейвлет: | |||
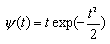 |
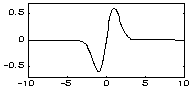 |
||
| MHAT - вейвлет ("Мексиканская шляпа" - Mexican hat): | |||
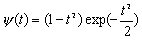 |
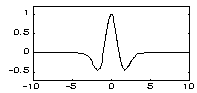 |
||
| Вейвлет Морле (образует комплексный базис): | |||
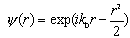 |
 |
||
На практике чаще приходится иметь дело с сигналами, заданными не аналитическими функциями, а с дискретным набором данных, определенном на конечном временном интервале. В этом случае принимается, что при Tk?t
Выше приведены примеры часто используемых вейвлетов (см. таблицу). Выбор того или иного класса анализирующих функций диктуется спецификой задачи, тем, какую информацию нужно извлечь из сигнала. В ряде случаев с помощью различных вейвлетов можно более полно выявить особенности анализируемого сигнала.
Спектр вейвлет-преобразования одномерного сигнала представляет поверхность в трехмерном пространстве. Обычно изображение спектра выполняется путем проектирования линий постоянного уровня поверхности на плоскость с переменными: параметрами сдвига (по оси абсцисс) и масштабом (по оси ординат), с градиентной заливкой оттенками серого цвета между линиями. В данной работе выбран вариант закраски, при котором область максимума имеет белый цвет, а минимума - черный. Используется также метод представления структуры спектральных данных с помощью "скелетона" - линий локальных экстремумов поверхности W(a,b) .
На приведенных ниже графиках представлены результаты расчета спектров вейвлетпреобразования временных рядов, построенных на основе функциональных зависимостей. Ряды рассчитывались на конечном интервале времени. В качестве анализирующего вейвлета использовался MHAT-вейвлет. Верхняя часть рисунка - исследуемый сигнал, средняя - изолинии поля W(a,b), нижняя - скелетон спектра. Изображены как линии локального максимума, так и минимума. В седловых точках поверхности происходит слияние линий.
Сигнал, представленный на рис. 1, является простым гармоническим колебанием. Картина линий уровня указывает на периодический характер сигнала и в мелкомасштабной области представляет регулярную систему ячеек с поочередно повторяющимися значениями максимума и минимума поля W(a,b), положение которых соответствует максимумам и минимумам сигнала. Граница раздела ячеек совпадает с положением нулей f(t).
Вертикальный размер ячеек определяет масштаб, отвечающий периоду колебаний. Постоянство расстояний между линиями скелетона также указывает на синусоидальный характер сигнала. Искажение формы ячеек вблизи границ обусловлено краевыми эффектами вследствие конечности исследуемого ряда. Крупномасштабная часть спектра содержит малые значения коэффициентов и в данном случае не информативна.
В данном случае имеется возможность проверки результатов численного расчета спектра вейвлет-преобразования и его качественной интерпретации. Выполняя интегрирование (3) для функции Y(t)= sin(wt), получаем
Таким образом, спектр для гармонического сигнала также является синусоидальным колебанием по переменной параметра сдвига, модулированной зависимостью
от масштаба (x=aw). Формула (8) объясняет все отмеченные выше особенности поведения спектра в центральной части рис. 1, свободной от влияния границы сигнала (разбиение на ячейки фиксированного размера, параллельность линий скелетона). Выбирая в качестве характерного масштаба значение, при котором
(рис.2), находим размеры ячеек:
С точки зрения Фурье-преобразования, эти два сигнала неразличимы. Вейвлет-анализ выявляет два характерных масштаба, периодичность следования ячеек смены знака указывает на периодический характер сигналов, их пространственное распределение показывает специфику каждого из сигналов. Постоянство расстояний между линиями экстремумов и их параллельность свидетельствуют, что составляющие сигнала - два гармонических колебания разных частот. Скелетон также дает дополнительную к картине изолиний информацию для уточнения размеров масштабов и периодов колебаний.
Сигнал, является суммой синусоиды и случайного сигнала той же амплитуды. Рисунок иллюстрирует фильтрационные свойства вейвлет-преобразования. Высокочастотные составляющие результирующего сигнала в спектре сосредоточены в основном в области малых значений масштаба, выше представлена несколько искаженная ячеистая структура, характерная для гармонических колебаний. Усредняя расстояния между линиями экстремумов, можно оценить период исходного синусоидального колебания.
Структура скелетона четко отслеживает синусоидальную составляющую сигнала даже в области очень малых значений коэффициентов и позволяет найти период колебаний. Картина линий уровня уточняет, что имеет место уменьшение амплитуды с ростом времени.
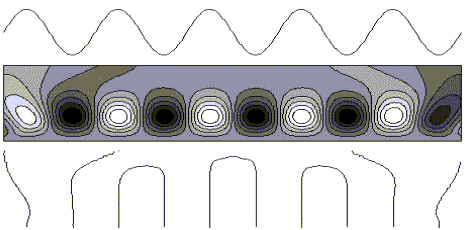
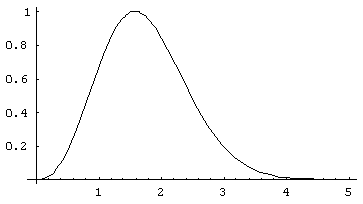
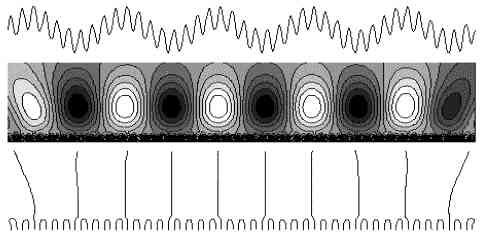
Рис.1. Сигнал - синусоида.
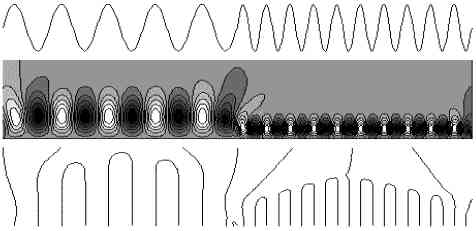
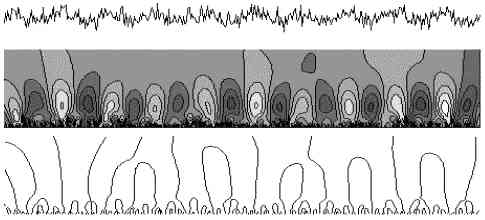
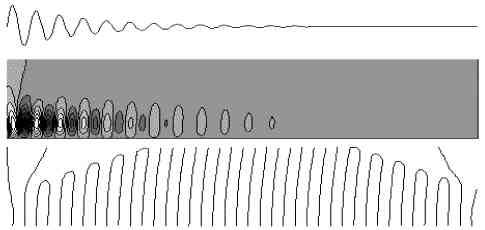
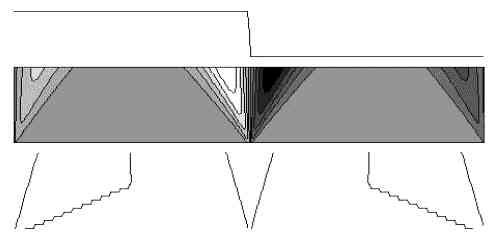
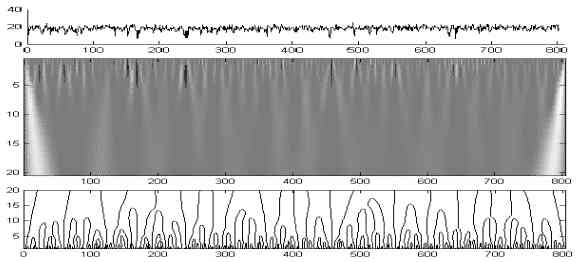
Рис. 2. График зависимости y(x)/ymax