
Источник: http://www.chipinfo.ru/literature/chipnews/200206/3.html
В. Стешенко, Р. Загидуллин, С. Карутин
Анализ сигналов и систем. Пакет SystemView компании Elanix. Занятие 2. Моделирование элементов радиоприемных устройств
В предыдущем занятии цикла мы рассмотрели первые шаги работы в пакете SystemView компании Elanix. Продолжим знакомство с пакетом на примере моделирования некоторых элементов радиоприёмных устройств.
В принципе, моделирование радиоприёмных устройств необходимо для определения таких их характеристик, как определение рабочего отношения сигнал/шум (ОСШ), пороговой чувствительности и т.п. Не менее важно всесторонне исследовать работу сердца любого приёмника–демодулятора. В этом занятии цикла мы рассмотрим некоторые приёмы моделирования демодуляторов сигналов.
Рассмотрим моделирование цифрового демодулятора сигналов с частотной манипуляцией. Рассматриваемый демодулятор относится к классу разомкнутых систем, что означает отсутствие петли обратной связи. В этой связи он обладает высоким быстродействием, при его работе отсутствуют пропуски сигнала из-за срыва слежения.
Демодулятор предназначен для преобразования исходного модулированного радиосигнала в последовательность прямоугольных импульсов, появляющихся с частотой следования символов и обладающих той же полярностью. Частота исходного радиосигнала равна f = f0 – f/2, если передаётся символ "0", и f = f0 – f/2, если передаётся символ "1"; при этом fTC, где TC - длительность символа (индекс модуляции - единица, сигнал без разрыва фазы). Таким образом, измерение разности f – f0 - это и есть та операция, которую должен осуществлять детектор. Можно показать, что при наличии отсчётов квадратур исходного радиосигнала: Sk и Ck, k = 0, 1, 2 и так далее, величина (f – f0)k может быть вычислена следующим образом:

Данное выражение по сути представляет собой не что иное, как оценку мгновенной частоты текущего сигнала как производной фазы сигнала. Такой подход обеспечивает некоторую инвариантность к входным параметрам схемы и позволяет избежать ряда проблем, возникающих при использовании замкнутых схем демодуляторов сложных сигналов.
Рассмотрим модель детектора ЧМ-сигнала в System View. Общий вид модели представлен на рис. 2.
Рисунок 1. Общий вид модели детектора ЧМ-сигнала
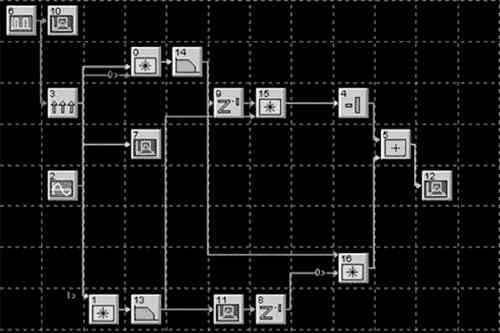
На рис. 1 следует выделить блоки, отвечающие за формирование ЧМн-сигнала и собственно демодулятор. По-следовательность модулирующих импульсов формирует генератор прямоугольных импульсов 6, с его выхода сигнал поступает на частотный модулятор 3, после чего формируются синфазная и квадратурная составляющие сигнала. Собственно демодулятор состоит из фильтров низких частот (13,14), элементов задержки (8,9), перемножителей (15,16) и вычитателя.
Настройка параметров модели показана на рис. 2.
Рисунок 2. Настройка параметров модели
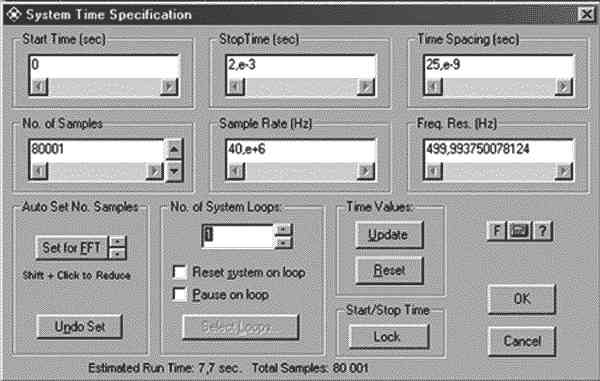
В окне Start Time вводим время начала моделирования, Stop Time — его завершение. Следует разумно подходить к выбору частоты дискретизации (sample rate), помня о возможных искажениях результатов моделирования за счёт её неправильного выбора. Следует отметить, что число отсчётов удобно выбирать кратным степени двойки, используя кнопки меню Set for FFT, что облегчает вычисление спектральных характеристик сигнала.
На модулятор поступают сигналы в форме меандра.
Таким образом, на выходе модулятора получаем сигнал, спектр которого показан на рис. 3. Хорошо заметно подавление несущей и две линии, соответствующие частотам нулей и единиц.
Рисунок 3. Спектр выходного сигнала модулятора

Модулированный радиосигнал, имеющий такой спектр, поступает на детектор ЧМн-сигнала, общая схема которого дана на рис. 2. Данный блок преобразует этот сигнал в последовательность прямоугольных импульсов, показанную на рис. 4.
Рисунок 4. Сигнал на выходе демодулятора
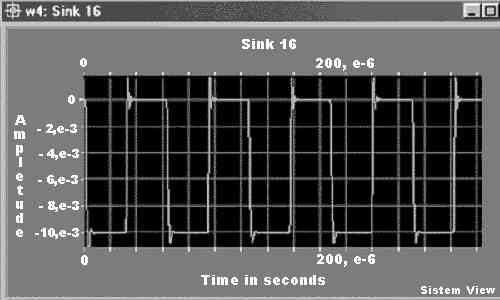
Следует заметить, что пока мы не рассматриваем вопрос о выделении тактовой частоты — это тема одного из следующих занятий. В принципе для решения этой задачи возможно использование схемы ФАПЧ.
Как видим, работа в системе достаточно логична и понятна.
Рассмотрим некоторые инструменты пакета SystemView, применяемые при анализе систем. На рис. 8 показана панель инструментов окна анализа (Analysis Window Toolbar).
Рисунок 5. Панель инструментов окна анализа

В таблице приведено описание её кнопок.
Рассмотрим ещё одну схему, часто применяемую для построения демодуляторов — широко известную схему Костаса. Схема Костаса второго порядка (Second-Order Costas Loop) показана на рис. 6.
Рисунок 6. Схема Костаса второго порядка

Схема Костаса входит в состав примеров, поставляемых в комплекте поставки SystemView. Она используется как демодулятор фазоманипулированных сигналов. Входной сигнал представляет собой фазоманипулированный сигнал, модулированный бинарным псевдослучайным сигналом. Формируемый сигнал ошибки представляет собой произведение синфазного и квадратурного сигналов I и Q. Отметим, что схема Костаса является одним из наиболее часто применяемых на практике демодуляторов фазоманипулированных сигналов, однако к её принципиальным недостаткам относится так называемая возможность работы в обратном режиме — то есть ошибочная (с точностью до наоборот) идентификация нулей и единиц цифрового потока. Для устранения этого эффекта приходится идти на усложнение протокола передачи данных.
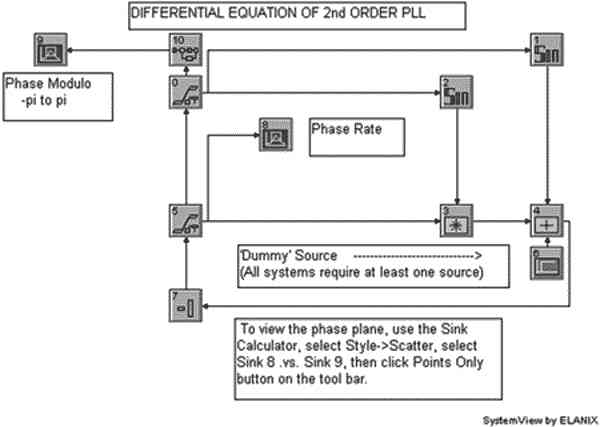
Рассмотрим моделирование системы фазовой автоподстройки частоты второго порядка. Система ФАПЧ описывается дифференциальным уравнением
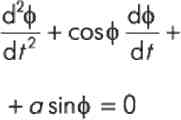
Схема ФАПЧ приведена на рис. 7. Она состоит из блока 10, приводящего фазу к диапазону от -p до p, а также остальных блоков, моделирующих уравнение 1. Отметим, что в данной схеме используется пустой источник (Dummy Source), поскольку попытка запустить схему без источника закончится неудачей — в схеме должен присутствовать хотя бы один источник сигнала. Данная схема "в лоб" моделирует уравнение 1 и в принципе не является наилучшей моделью ФАПЧ. В следующих занятиях мы рассмотрим особенности применения моделей ФАПЧ и ЧАП (частотной автоподстройки частоты) для моделирования элементов синтезаторов частот и демодуляторов сигналов.
Рисунок 7. Схема ФАПЧ
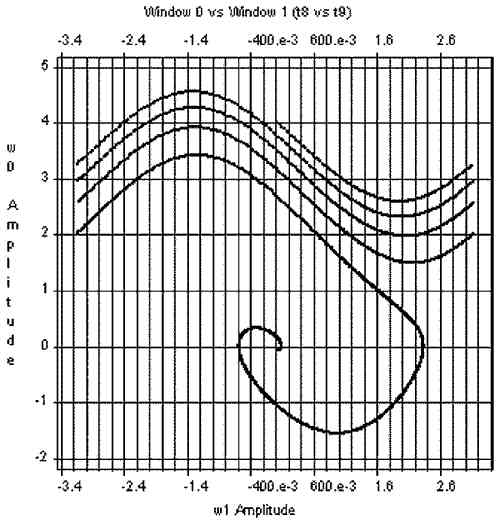
Наглядное представление о работе системы ФАПЧ даёт использование метода траекторий на фазовой плоскости, представляющих собой частотную ошибку относительно фазовой ошибки.
На рис. 8 приведена фазовая плоскость ФАПЧ. Вертикальная ось соответствует частоте, а горизонтальная — фазе, приведённой к диапазону [-p,p]. Перед синхронизацией контур пропускает несколько циклов. Для просмотра динамики можно использовать функции анимации в окне анализа.
Рисунок 8. Фазовая плоскость системы фазовой автоподстройки частоты второго порядка
Следует отметить, что помимо диаграмм на фазовой плоскости, одним из действенных методов оценки качества замкнутых систем является анализ их характеристик во временной области (динамика переходных процессов при слежении и срыве), а также анализ в спектральной области — оценки спектра фазового рассогласования и т.п.