

In the operation research we have to come across with the work analysis of the peculiar systems called the systems of mass service (SMS). For an example they are telephone systems, repairing workshops, ticket offices, information offices, shops, hairdressers and others. Each SMS consists of some servicing units which we will call servicing canals. In case of “canals” may figure connection lines, work places, devices, railways, lifts, cars and others. The systems of mass service may be one-canal and multi- canal ones. Each SMS is intended for the servicing of an application flow (or “demands”) received on SMS at any occasional time. The servicing of received application lasts some occasional time, and then the canal is free and ready to receive to get another one. The occasional character of application flow leads to the accumulation of the large application quantity on the SMS entry at some periods of time. These applications form a queue or they leave the SMS unserved. At other periods of time the SMS will work with under loading or idle at all. Each system of mass service, depended on the canal quantity and their productivity with the character of application flow, has a blotting capability which allows it to manage with application flow more or less successfully. The subject of mass service theory is the definition of dependence between the character of application flow, canal number, and their productivity, SMS work rules and service effectiveness. For the description of a food shop function the SMS with time limit expectation suits more. Let’s consider such SMS staying in markovskaja scheme. Let’s suppose that there is a canal SMS with expectation in which the quantity of places at the queue is not limited but the time in the application queue is limited by the occasional term T with the average meaning T . So each application is influenced by “leaving flow” with the intensity

Condition diagram is shown on Fig. 2.1
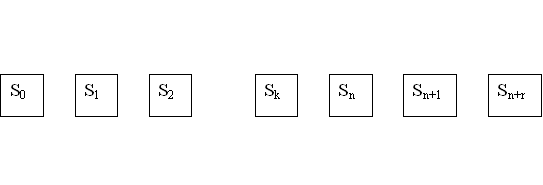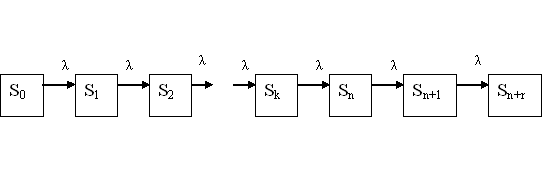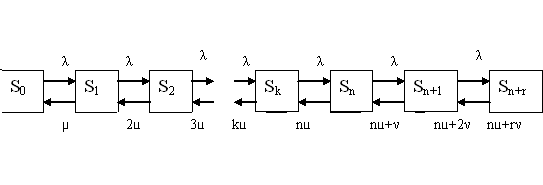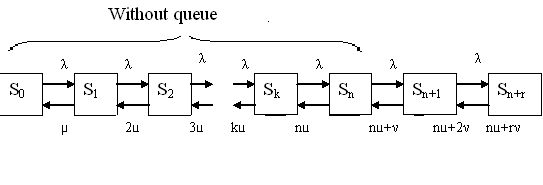


r = 1* pn+1 + 2*pn+2+…+r*pn+r+… .
Each application is influenced by “leaving flow” with intensity v. it means that from average application number r in the queue on average vr applications at a time unit will leave unserved: at a time unit on average will be served

applications. Relative blotting capability of SMS will be

The average number of busy canals z will be received dividing absolute blotting capability into m:


We can find the average number of busy canals included into this formula as mathematic expectation of occasional value Z which has the meaning 0, 1, 2, …., n with probabilities…
Z= 0*p0+ 1*p1+2*p2+…+ n*[1-(p0 +p1 +…+pn-1)]=p1+2*p2+…+ n*[1-(p0 +p1 +…+pn-1)] 2.7
Note that in formula (2.1) the sum of unlimited row is figured which is not progression. But this sum is counted approximately and easy enough as the row parts decrease quickly with their number increasing. As the approximate meaning for unlimited sum we will take the sum of the final figure г – 1parts but the rest is estimated as following:

In the conclusion we note that if in the formulas (2.1) we pass to the limit v - 0 (b- 0) in case ….p n the formulas (6.10) are received of the previous paragraph, so “impatient applications” will became “patient”.
We come across with the necessity of being in expectation condition in all person practical activities. Such situations occur in queues to ticket offices, big airports, on the telephone stations in case if the line is engaged, in repairing workshops in case expecting lathe and equipment repairing and in supply-sale organizations in unloading or loading of transport means expectation. In all these cases we deal with mass servicing. The mass servicing theory is involved in such situations studying.
The occasional character of application flow, but in general case and the servicing duration, leads to the occasional process in the system of mass servicing.
It is necessary to study the occasional process in the system, to describe it mathematically to give the recommendation in the rational organization of this process and to make sensible demands to SMS. The mass servicing theory deals with such problems.