УДК 53.01 : 004.94

Доклад на региональную студенческую конференцию "Физика и научно-технический прогресс" (ФиНаТ-2005)

Шевченко Л.В., старший преподаватель кафедры физики

Садыкбаев А.В.

 

Донецкий национальный технический университет

Моделирование физических процессов

 

Цель данной работы – практически проверить теоретические знания о математическом маятнике. Для этого воспользуемся построением компьютерной модели математического маятника. Фактически, мы проводим пассивный вычислительный эксперимент.

Представленная модель математического маятника создана в программном комплексе MatLab/Simulink. Модель описывает самый простой вариант математического маятника, в котором тело подвешено на нерастяжимой нити и колебания в системе незатухающие.

Прежде чем описывать математическими формулами модель маятника, нужно представить как выглядит исследуемое тело. На рисунке 1 показан исследуемый маятник .

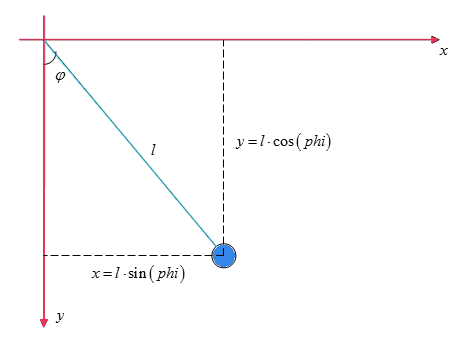
Рис. 1

 

В данный момент тело, подвешенное на нерастяжимой нити длинной , отклонено на некоторый угол  от положения вертикали. Легко найти составляющие угла отклонения :

     

В дальнейшем, при построении модели математического маятника будем использовать вместо греческого обозначения угла  сочетание . Это связано с тем, что при проектировании модели в системе моделирования нельзя пользоваться греческими буквами.

Для удобства, возьмём нить длиной 1 метр. Тогда:

            

Перед тем как приступить непосредственно к моделированию, нам нужно описать поведение математического маятника. В этом заключается основное отличие пассивного вычислительного эксперимента от активного. В данной работе мы работаем с моделью, все необходимые свойства которой уже известны заранее [4].

Опишем движение маятника. Как известно, уравнение движения математического маятника имеет вид:

,

где   – угол отклонения маятника от положения равновесия . Но в такой форме, уравнение не устраивает нас. Найдём из уравнения угол :

В данном уравнении мы видим зависимость изменения угла отклонения маятника с течением времени. Теперь, после того, как у нас есть уравнения, описывающие движения маятника, можно приступить к созданию программной модели. В системе моделирования Simulink, все модели строятся из блоков, которые соединяются между собой соединительными линиями [1, 2]. Готовая модель показана на рисунке 2.

 

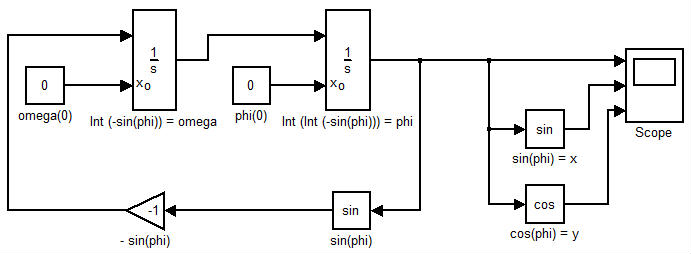
Рис. 2

 

Каждый блок модели подписан:

  – интегратор;

 – константа «1»;

 – изменение знака поступающего выражения на противоположный;

 – блок тригонометрических функций (, ,  и т.д.);

 – блок визуализации.

 

На схеме видно, что процесс вычисления нового значения угла отклонения итеративен. Сама схема условно разделена на 2 части (см. рис. 3): часть вычисления значения угла и часть вывода результатов моделирования в качестве графика.

 

Рис. 3

 

При получении нового значения угла , результаты поступают на блок визуализации , который по полученным значениям строит графики зависимости изменения угла от времени.

После сборки схемы модели, нужно запустить процесс моделирования нажатием на кнопку :

 

 

 

После завершения процесса симуляции, результаты работы можно увидеть в блоке визуализации  (см. рис. 4) [3].

 

 

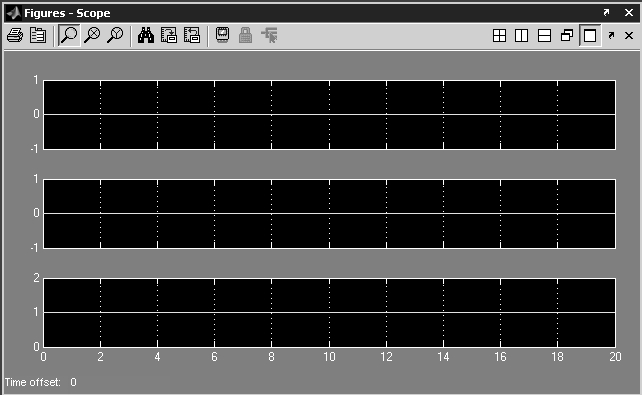
Рис. 4

 

 

Как видно из рисунка 4, графиком колебаний математического маятника в таком случае является прямая линия. Иными словами положение маятника на протяжении всего времени не изменяется. В чём же дело? Если взглянуть на схему модели, то видно, что на интеграторы подаются начальные условия  (угловая скорость) и . Значит, нужно сдвинуть маятник с места. Сделать это можно или задав начальную угловую скорость отличную от нуля, или начальный угол отклонения отличный от нуля. Выбирая между двумя способами изменения положения маятника, будем руководствоваться принципами наглядности. И действительно, процесс отклонения и отпускания нити с привязанным на конце грузом более нагляден, чем процесс придания скорости телу.

Изменим начальный угол отклонения маятника, как показано на рисунке 5.

 

 

Рис. 5

 В системе Simulink углы задаются в радианах. Изменения показаны на рисунке 6.

Рис. 6

 

Результатом симулирования будет графики, изображённые на рисунке 7.

Рис. 7

 

 

На трёх графиках показано изменение угла отклонения , горизонтальную составляющую движения  и вертикальную составляющую движения . Для отображения результатов выбран авто масштаб.

Однако использование специализированных сред моделирования не является единственно возможным путём моделирования поведения маятника. Для осуществления задачи, можно было воспользоваться любым языком программирования и тогда бы результаты выводились в той форме, в которой пожелал бы программист. Но такой подход сильно усложняет задачу и не позволяет сосредоточиться только на процессе моделирования.

На рисунке 8-9 изображена демонстрационная программа моделирования математического маятника в среде Macromedia Flash 6.0.

 

 

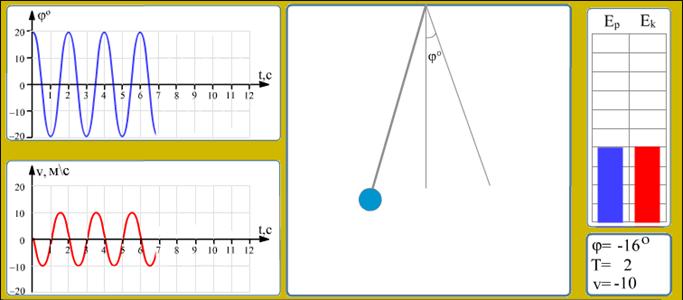
Рис. 8

Данная модель демонстрирует процесс гармонических колебаний математического маятника. Выводятся графики зависимости угла отклонения от вертикали и скорости движения от времени. В виде изменяющихся диаграмм показаны значения кинетической и потенциальной энергий. В каждый момент времени показаны значения угла отклонения и скорости. Для расчетов взяты следующие значения: длина нити-1 метр, угол первоначального отклонения - 20 градусов.

 

 

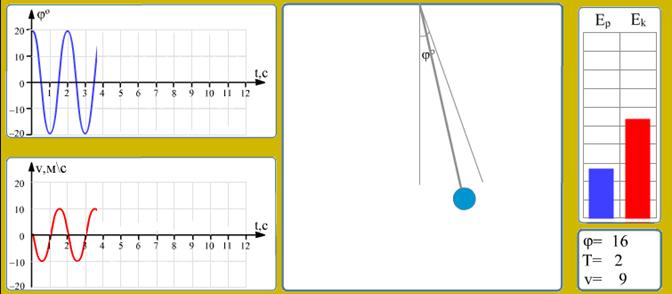
Рис. 9

 

Литература:

1. Дж. Дэбни, Т. Харман Simulink 4. Секреты мастерства - Бином. Лаборатория знаний, - М., 2003, 403 стр.
2. В. П. Дьяконов Simulink 5/6/7. Самоучитель, - ДМК пресс, - М., 2008, 784 стр.
3. Г. А. Бордовский, А. С. Кондратьев, А. Д. Р. Чоудери Физические основы математического моделирования - Академия, - М., 2005, 320 стр.
4. Д. В. Алексеев Компьютерное моделирование физических задач в Microsoft Visual Basic - Солон-Пресс, - М., 2004, 525 стр.

© Садыкбаев А.В., Шевченко Л.В., 2005