
Щеглов Максим Ігорович
Факультет: Обчислювальної техники та інформатики
Спеціальність: Програмне забезпечення автоматизованих систем
Тема магістерьскої дисертації: "Аналіз та оцінка ефективності паралельних багатокрокових блокових методів розв’язання ЗДР на кластері"
Науковий керівник: Фельдман Лев Петрович професор, д.т.н.
Реферат
- Введення
- Актуальність теми
- Мета й задачі розробки та дослідження
- Предмет розробки та дослідження
- Практичне значення отриманих результатів
- Паралельні багатокрокові блокові методи чисельного рішення задачі Коші для ОДУ
- Опис паралельних багатокрокових блокових методів чисельного рішення завдання Коші для ОДУ
- Погрішність апроксимації блокових методів
- Оцінка ефективності паралельних багатокрокових блокових методів чисельного рішення завдання Коші для ОДУ
- Висновки
- Список використаної літератури
Аналіз та оцінка ефективності паралельних багатокрокових блокових методів розв’язання ЗДР на кластері
Введення
Одним з найважливіших напрямків розвитку обчислювальних технологій є паралельні обчислення. В останні роки максимальна продуктивність існуючих паралельних обчислювальних систем істотно зросла. Радикально змінилася технологічна база й архітектура. Але головною перешкодою до впровадження практично всіх паралельних архітектур є відсутність паралельних алгоритмів. Доводиться шукати зовсім нові методи для рішення різних завдань, які орієнтовані на ефективне використання в багатопроцесорних системах, або модернізувати існуючі алгоритми. Вже в найближчому майбутньому перспективи розвитку суперкоппьютерів будуть визначатися успіхами не стільки електроніки, скільки обчислювальної математики.Мова, у першу чергу, іде про звичайні диференціальні рівняння та системи диференціальних рівнянь, які є основою сучасних наукових і інженерних завдань. Багато чисельних методів рішення доводиться переглядати, а від деяких повністю відмовлятися. У той же час, цілий ряд питань, які були несуттєві або взагалі не виникали при проведенні послідовних обчислень, придбали виняткову важливість для ефективного й правильного використання обчислювальних систем.
Досвід експлуатації сучасних високопродуктивних комп'ютерних систем показав, що ефективність їхнього застосування істотно залежить від узгодження структури паралельних обчислювальних систем із класом розв'язуваних завдань і використовуваних чисельних методів. Ці обставини послужили основою для адаптації відомих і пошуку нових методів рішення систем звичайних диференціальних рівнянь на паралельних системах з MІMD архітектурою.
Актуальність теми
За допомогою диференціальних рівнянь і систем диференціальних рівнянь можна описати велику кількість фізичних, механічних, біологічних, економічних і.т.п. явищ. Отримані моделі, як правило, являють собою диференціальні рівняння, рішення яких на однопроцесорних комп'ютерах за прийнятний час неможливо. Звідси треба, що розробка паралельних методів рішення задачі Коші є актуальною задачею.Мета й задачі розробки та дослідження
Ціль роботи: аналіз рішення задачі Коші багатокроковим паралельним блоковим методом на обчислювальному кластері, розробка й реалізація програмної системи, що дозволяє одержати рішення даної задачі.Задачі: вивчення багатокрокових паралельних блокових методів рішення задачі Коші, рішення задачі Коші багатокроковим паралельним блоковим методом на обчислювальному кластері з використанням Microsoft Visual Studio 2005 і технології Message Passing Interface (MPI).
Предмет розробки та дослідження
Предмет розробки й дослідження: Предметом досліджень є паралельні блокові методи рішення задачі Коші на обчислювальному кластері Microsoft Windows Compute Cluster Server 2003.Практичне значення отриманих результатів
Отримані результати дадуть можливість оцінити ефективність паралельних блокових методів рішення задачі Коші на обчислювальному кластері. Розроблена програмна система може бути використана для рішення задачі Коші багатокроковим паралельним блоковим методом.Паралельні багатокрокові блокові методи чисельного рішення завдання Коші для ОДУ
У даній главі розглядаються основи розпараллелювання багатокрокових алгоритмів рішення завдання Коші для ОДУ. Виведемо формули й знайдемо наближене рішення завдання Коші для диференціального рівняння першого порядку:y'=f(x,y)
(1.1)
y(x0)=y0
(1.2)
- i =0,1,…,k - номер точки для кожного блоку;
- tn,i - точка n –го блоку з номером i;
- крапка tn,0 - початок блоку n, а tn,k – кінець блоку;
- tn,k = tn+1,0 .;
- початкова точка в блок не включається.
Опис паралельних багатокрокових блокових методів чисельного рішення завдання Коші для ОДУ
У випадку багатокрокового блокового методу початковий блок буде містити крапки сітки, у яких початкові значення наближеного рішення необхідні для продовження розрахунків.Схема розбивки на блоки для m-крокового k-точкового методу представлена на рисунку 1.1.

Рисунок 1.1 - Схема розбивки на блоки для m-крокового k-точкового методу
(Анімація складається з 4 кадрів, 78 Кб із затримкою в 1с між кадрами; затримка до повторного відтворення становить 2с; кількість циклів відтворення - 7)
У загальному випадку рівняння багатокрокових різницевих методів для блоку з k точок при використанні обчислених значень наближеного рішення в m попередньому блоку вузлах, можна записати у вигляді:
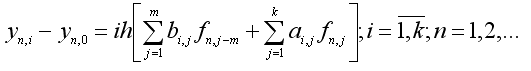
(1.3)
Визначити коефіцієнти ai,j и bi,j можна апроксимуючи подінтегральну функцію з одним змінним f(x,y(x)) алгебраїчним інтерполяційним багаточленом Лагранжа Lk(t), що у вузлах xn,j-m приймає значення f(xn,j-m,y(xn,j-m)), j=1,2,...,m+k. Далі необхідно проінтегрівати його в межах (tn, tn+iτ), i=1,k
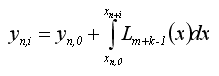
(1.4)
У підсумку будуть отримані необхідні формули.
Для обчислення наближених значень рішення завдання Коші коллокаціонним багатокроковим блоковим методом необхідно вирішити нелінійну систему рівнянь (1.3). Можна для цього використати наступний ітераційний процес:
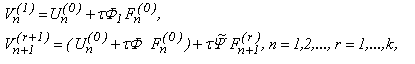
(1.5)
Закріпимо кожний процесорний елемент за точкою n-го блоку, що обчислюється. Тоді кожний з k процесорів спочатку буде обчислювати значення початкового вектора за методом Адамса-Башфорта.
Далі кожний процесор буде знаходити відповідного вектора зі значеннями правих частин fn,j=f(tn+jτ,un,j)) . Після чого буде здійснюватися обмін між процесорними елементами для виконання подальших обчислень. Потім по заданим формулам будуть визначатися значення вектора наближеного рішення. Якщо кількість процесорів буде менше, ніж розмірність блоку, то деякі процесорні елементи будуть послідовно обчислювати значення декількох крапок блоку, що в підсумку збільшить загальний час обчислень.
При рішенні системи диференціальних рівнянь можливі два варіанти розподілу процесорів:
- для кожного рівняння виділяється P1=P/k процесорів, де P- загальне число процесорів, а k- число рівнянь у системі. P1 процесорів беруть участь у паралельному обчисленні значень блоку: m/P1 значень крапок блоку обчислюються на кожному із процесорів
- для кожного блоку виділяється P1=P/m процесорів, де P- загальне число процесорів, а m- число крапок у блоці. k/P1 рівнянь системи обчислюються на кожному із процесорів
- вектор початкових наближень функції Ui,j;
- вектор значень ОДУ для сіткових функцій у вузлах попереднього блоку Fi,j;
- вектор значень елементів ψ i,j , що є і-им стовпцем матриці Ψ;
- вектор значень елементів φ i,j , що є і-им стовпцем матриці Φ;
- вектор значень елементів F i,j , що є і-ом рядком матриці F.
Погрішність апроксимації блокових методів
Коефіцієнти ai,j и bi,j вибираються таким чином, щоб різницеве рівняння (1.3) апроксимувало диференціальне рівняння з досить гладкою правою частиною з деяким порядком s. Це означає, що нев'язання ρ , що виходить після підстановки точного рішення y(x) диференціального рівняння в різницеве рівняння (1.3).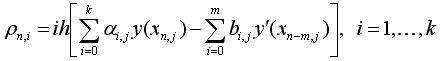
(1.6)
Величина
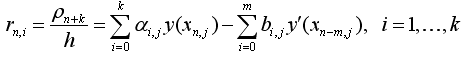
(1.7)
Називається погрішністю апроксимації диференціального рівняння різницевим рівнянням (1.3).
Якщо скористатися формулою Тейлора для y(xn+i) и y'(xn+i) , то погрішність апроксимації буде мати вигляд:
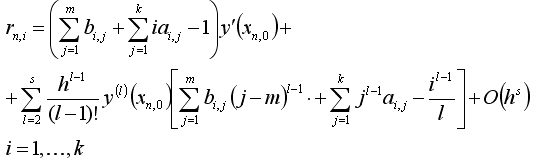
(1.8)
З (1.8) видно, що для того, щоб величина rn,i мала порядок O(h5) необхідне виконання умов
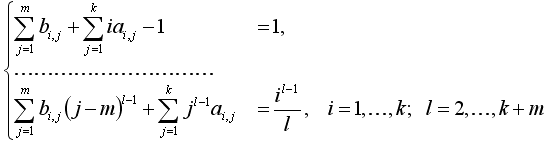
(1.9)
Оцінка ефективності паралельних багатокрокових блокових методів чисельного рішення завдання Коші для ОДУ
Критеріями оцінки паралельних алгоритмів, як правило, виступають дві величини:- прискорення Sp
- ефективність Ep
- T1- час виконання послідовного алгоритму;
- Tp – час виконання паралельного алгоритму на k процесорів;
- Tf – час обчислення значення функції f(t,x);
- Tсл – час виконання операції додавання;
- Tум – час виконання операції множення;
- Tоб – час передачі числа сусідньому процесору.
Sp(n)=T1(n)/Tp(n)
(1.10)
Ефективність (effіcіency) використання паралельним алгоритмом процесорів при рішенні завдання визначається співвідношенням
Ep(n)=T1(n)/(pTp(n))=Sp(n)/p
(1.11)
Для оцінки прискорення m-крокового k-точкового блокового методу зрівняємо час його виконання на мультипроцесорній системі з часом виконання алгоритму m-крокового методу Адамса-Башфорта на однопроцесорній ЕОМ. Метод Адамса-Башфорта можна розглядати як багатокроковий однокрапковий блоковий метод. Послідовне k-кратне застосування формул Адамса-Башфорта дозволяє обчислити наближене рішення в тих же k вузлах блоку, у яких паралельно за k ітерацій може бути обчислене рішення m-кроковим k-крапковим блоковим методом. У цьому випадку час обчисленнь буде приблизно однаковим. Точність наближеного рішення, отриманого m-кроковим k-крапковим блоковим методом, має порядок O(τm+k), а точність наближеного рішення, отриманого по m кроковій формулі Адамса-Башфорта, має порядок O(τm+1).
Для того, щоб одержати рішення з однаковою точністю для методу Адамса-Башфорта необхідно, щоб кроки сітки для методу Адамса-Башфорта й m-крокового k-крапкового блокового методу задовольняли умові
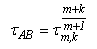
Наприклад: для рішення завдання 4-кроковим 4-крапковим блоковим методом обраний крок τm,k =0.01, тоді для забезпечення тієї ж точності рішення методом Адамса-Башфорта необхідно взяти крок τA,B =0.0063.
Час виконання послідовного алгоритму у всіх k вузлах:
T1=k2*tf+(k+1)*(tум.+tсл.)
(1.12)
Час паралельного обчислення наближених значень рішення на лінійці процесорів:
Tk=(k+1)*tf+(3k2+2k+1)*tсл.+(3k2+3k+1)*tум.+k(2k+1)об.
(1.13)
Слід зазначити, що на динамічні характеристики паралелізму впливають латентність і час передачі одного слова. Отримана залежність коефіцієнта ефективності від латентності є обратнопропорційною (при зменшенні величини латентності збільшується эффективнность алгоритму рішення завдання) і наведена на рисунку 1.2.
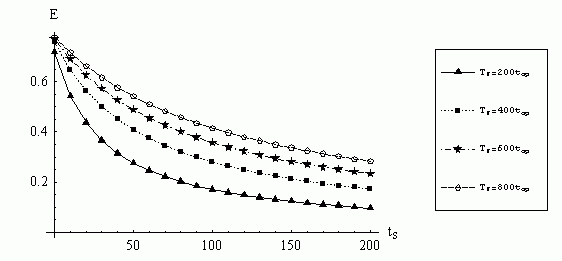
Рисунок 1.2 - Залежність коефіцієнтів ефективності паралельного багатокрокового блокового методу від величини латентності, ts
З ростом величини латентності час, затрачуваний на обмін даними між процесами збільшується, а ефективність паралельних обчислень зменшується. При розрахунку прискорення й ефективності багатокрокового блокового методу найбільший вплив на показники робить час обчислень правої частини рівнянь, тому що час виконання арифметичних операцій і обміну значно менше часу обчислення правої частини. Залежність коефіцієнтів прискорення й ефективності від часу обчислення правої частини рівняння Tf і числа точок блоку k наведені на рисунках 1.3, 1.4.
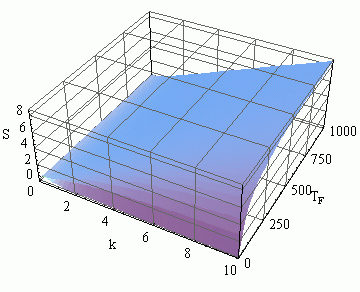
Рисунок 1.3 - Залежність коефіцієнта прискорення паралельного багатокрокового блокового методу від часу обчислення правої частини, Tf і числа точок блоку k
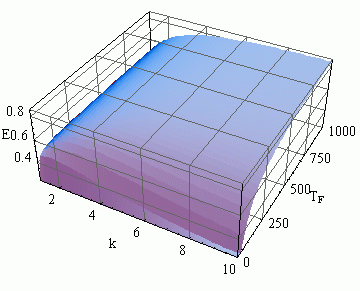
Рисунок 1.4 - Залежність коефіцієнта ефективності паралельного багатокрокового блокового методу від часу обчислення правої частини, Tf і числа точок блоку k
Прискорення k-точкового багатокрокового паралельного алгоритму можна вважати приблизно рівним
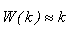
а ефективність буде дорівнювати
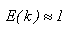
При цьому характеристики паралелізму в системах з кільцевою структурою виявляються гірше, ніж у системах з топологією гіперкуб і тор, що свідчить про сильний вплив час обміну даними між процесорами в паралельних обчислювальних системах. Між часом обчислення правої частини й ефективністю існує пряма залежність: при збільшенні трудомісткості обчислень правих частин, ефективність розглянутих методів збільшується. Також слід зазначити, що у зв'язку з тим, що число точок блоку пов'язане із числом використовуваних процесорів, при збільшенні числа крапок у блоці зростає коефіцієнт прискорення S і зменшується коефіцієнт ефективності E[4].
Висновки
У даному розділі були розглянуті багатокрокові блокові методи рішення задачі Коші для звичайних диференціальних рівнянь, показана погрішність апроксимації, наведені оцінки ефективності даних методів.Надалі при виконанні магістерської дисертації буде розроблена програмна система для рішення задачі Коші багатокроковим паралельним блоковим методом. Використання розроблювальної програмної системи дозволить оцінити показники ефективності й точність паралельного рішення задачі Коші досліджуваним методом.
Список використаної літератури
- Гергель В.П., Стронгин Р.Г. Основы параллельных вычислений для многопроцессорных вычислительных систем. - Н.Новгород, ННГУ, 2001
- Хайрер Э., Нёрсетт С., Ваннер Г. Решение обыкновенных дифференциальных уравнений. Нежесткие задачи: Пер. с англ. – М.: Мир, 1990. – 512с.
- Фельдман Л.П. Сходимость и оценка погрешности параллельных одношаговых блочных методов моделирования динамических систем с сосредоточенными параметрами // Научные труды ДонНТУ. Серия: Информатика, моделирование и вычислительные методы, (ИКВТ-2000), выпуск 15: Донецк: ДонНТУ, 2000, с. 34-39.
- Дмитриева О.А. Модели отображения многошаговых алгоритмов на параллельные вычислительные системы с топологией гиперкуб//Науковi працi Донецького державного технiчного унiверситету. Серiя: Проблеми моделювання та автоматизації проектування динамічних систем, випуск 46: – Донецк:, 2002. с. 154-161.
- Фельдман Л.П., Дмитриева О.А. Разработка и обоснование параллельных блочных методов решения обыкновенных дифференциальных уравнений на SIMD-структурах. //Научн. тр. Донецкого государственного технического университета. Серия: Проблемы моделирования и автоматизации проектирования динамических систем, выпуск 29. – Севастополь: «Вебер», 2001. – с. 70-79.
- Kazufumi OZAWA, Susumu YAMADA “Parallel block methods for solving nonstiff equations with stepsize control“,Graduate school of information science, Tohoku University, 2006
- Воеводин В.В.,"Вычислительная математика и структура алгоритмов.".-М.: Изд-во МГУ, 2006.-112 с.
- van der Houwen P.J.,“Parallel Step-by-Step Methods”, CWI Amsterdam, 1991
- Самарский А.А., Гулин А.В. Численные методы.- М.: Гл. ред. физ.-мат. лит., 1989.– 432 с.
- Воеводин В.В. Математические основы параллельных вычислений. - М.: Изд-во МГУ, 1991. - 345 с.
http://window.edu.ru/window_catalog/pdf2txt?p_id=6579
http://repository.kulib.kyoto-u.ac.jp/dspace/bitstream/2433/60205/1/0944-2.pdf
http://www.parallel.ru/info/parallel/voevodin/
http://ftp.cwi.nl/CWIreports/1991/NM-R9116.pdf