Щеглов Максим Игоревич

Библиотека

---

Автор: Л.П. Фельдман, д-р техн. наук

Донецкий национальный технический университет

Украина, 83001, Донецк, ул. Артема, 66.

---

Параллельные коллокационные методы решения задачи Коши для обыкновенных дифференциальных уравнений

Постановка задачи

Доклад содержит обобщение результатов исследований [1-6], посвященных параллельным методам численного решения задачи Коши для системы обыкновенных дифференциальных уравнений и является продолжением ранее опубликованных работ [7-13]. В нем рассматривается применение интегро-интерполяционного метода вывода коллокационных разностных формул, как для последовательных, так и блочных одношаговых и многошаговых многоточечных разностных схем решения задачи Коши для обыкновенных дифференциальных уравнений. Предлагаемый подход является универсальным для получения разностных уравнения различных видов. Получаемые на основе такого подхода расчетные формулы для последовательных одношаговых многоточечных разностных уравнений эквивалентны неявным методам Рунге-Кутты (НРК), обладают меньшей вычислительной сложностью и являются весьма эффективными при решении жестких уравнений. Блочные одношаговые и многошаговые многоточечные разностные схемы обладают высокой точностью и легко распараллеливаются. Рассмотрены также методы оценки локальной погрешности и устойчивости полученных разностных схем и даны практические рекомендации параллельного их использования.

1. Коллокационные одношаговые и многошаговые разностные методы

При численном решения задачи Коши для обыкновенных дифференциальных уравнений

                                                                         (1)

понятие коллокации состоит в нахождении многочлена степени s, у которого в s заданных точках производные совпадают с векторным полем дифференциального уравнения. Получаемые на основе такого подхода расчетные формулы эквивалентны неявным методам типа Рунге-Кутты и используются для  жестких уравнений [4]. Для определения коэффициентов таблицы Бутчера НРК, соответствующего коллокационного метода вводят s - положительное натуральное число и  - вещественные числа на отрезке [0,1]. Затем определяют коллокационный многочлен v(t)  следующим образом:

  -  начальное условие,                                                      (2)

.                (3)

Численное решение задачи Коши для обыкновенного дифференциального уравнения задается при этом формулой:

.                                                                                     (4)

Если все узлы  различны, то имеет место следующая теорема.

Коллокационный метод (2)-(4) эквивалентен s-стадийному неявному методу Рунге-Кутты, у которого

,                                     (5)

где    являются базисными многочленами Лагранжа:

.                                                                               (6)

Метод коллокации позволяет достаточно просто получать формулы для различных неявных методов Рунге-Кутты. Выберем, например, следующие узлы коллокации:

.

Построим базисные многочлены для этих узлов. Используя (6), запишем базисные многочлены Лагранжа, соответствующие рассматриваемому пятистадийному методу. Определим коэффициенты неявных  коллокационных двухстадийных методов Рунге- Кутты по формулам (5). Таблица Бутчера имеет вид:

                                                       (7)

Вычисление значения приближенного решения дифференциального уравнения  в узле  по значению в узле , сводится в рассматриваемом методе к решению системы нелинейных уравнений порядка  s  относительно :

                                     (8)

и вычисления значения приближенного решения на очередном шаге по формуле:

                                                                       (9)

Рассмотренный метод можно назвать одношаговым s -стадийным одноточечным методом, поскольку по значению приближенного решения в одной точке  предыдущего узла  после решения нелинейной системы уравнений s-го порядка вычисляется приближенное решение  в очередной точке . Коллокационные формулы можно представить в другой форме, позволяющей строить как одношаговые, так и многошаговые многоточечные разностные методы. Обозначим через , соответствующее ему приближенное значение решения через и . Получим интерполяционный многочлен  по таблице { , }. Проинтегрируем уравнение (1) по t  получим:

                                                (10)

Заменив  в (10) функцию f(t,x)  на полином получим

                                                     (11)

систему нелинейных разностных уравнений для определения значений ,  приближенного решения задачи Коши (1). Например, варианту метода с точками коллокации  соответствуют следующие уравнения.

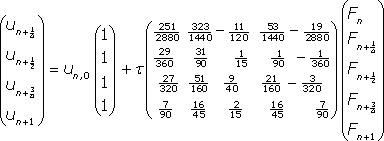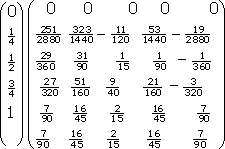,        (12)

Оценки погрешности аппроксимации уравнений (12) приведены ниже:

                             (13)

Матрица коэффициентов системы уравнений (12) совпадает с таблицей коэффициентов  таблицы Бутчера (7), поскольку они получены по одному и тому же интерполяционному многочлену. Для определения значения необходимо решить систему уравнений (12). При этом значения являются вспомогательным при решении. Поскольку коллокационный разностный метод (11) эквивалентен sстадийному неявному методу Рунге - Кутты, то условия устойчивости и области устойчивости для них совпадают. Отметим, что разностные уравнений, соответствующие неявным формулам Рунге-Кутта с равномерным шагом, совпадающие с приведенными выше коллокационными методами были получены с помощью N преобразования [14]. Используя интегро-интерполяционный метод можно получить многошаговые одноточечные s-стадийные коллокационные методы. Например, для метода с точками коллокации  разностные уравнения будут иметь вид:

Этот метод является двухшаговым одноточечным двухстадийным. Также можно получать разностные формулы с переменным шагом. Для метода с точками коллокации отношение шагов в соседних узлах равно . Приведем соответствующие уравнения:

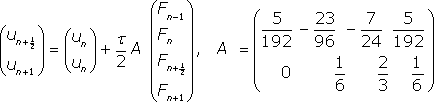                                    (14)

Рассмотренный выше подход построения коллокационных методов, может быть использован для построения блочных одношаговых по шаблону рис. 1 и многошаговых многоточечных методов по шаблону рис. 2.

Рис.1. Шаблон разностной схемы одношагового k-точечного блочного метода

Используя k  последовательных узлов основной сетки, т.е. положив,  построим по ним интерполяционный многочлен и найдем коэффициенты соответствующей им системы разностных уравнений. Приведем разностные уравнения одношагового четырехточечного метода, построенные по узлам

                                           (15)

Легко видеть, что матрица системы уравнений (15) получается из матрицы системы (12) умножением ее на 4, число равное отношению длин шагов соответствующих сеток. Приведенный метод представляет собой один из частных случаев одношаговых блочных методов. В общем случае разностные уравнения одношаговых блочных методов имеют вид:

, , .                                       (16)

В рассматриваемом случае, после решения системы уравнений (15) получим приближенные значения решения задачи в четырех последовательных узлах сетки. При этом вычислительные затраты будут теми же, что и в случае решения одношаговым одноточечным коллокационным методом (12) или соответствующему ему неявному методу Рунге-Кутты. Таким образом, одношаговый многоточечный коллокационный метод в k  раз эффективнее соответствующего одношагового одноточечного коллокационного метода при одинаковой их точности. Метод (15) относится к типу блочных методов, поскольку на каждом шаге решения разностных уравнений получается вектор значений приближенного решения в k  последовательных узлах сетки. Можно получить и более общие блочные коллокационные методы, выбрав в качестве точек коллокации , где m - целое неотрицательное число.

Рис.2. Шаблон m-шаговой k-точечной разностной схемы

Общий вид разностных уравнений многошаговых блочных методов:

.                                         (17)

Получим, например, коллокационный разностный метод со следующими узлами { }= {-2,-1,0,1,2,3}. Построим так же, как в предыдущем примере, по этим узлам интерполяционный многочлен и найдем коэффициенты соответствующей им системы разностных уравнений:

.

2. Устойчивость и сходимость блочных  методов

Одношаговые m = 1 и многошаговые m > 1 многоточечные блочные методы, определяемые формулами (16) и (17) всегда устойчивы по начальным данным. Это прямо следует из того, что решения однородной системы, соответствующей (16) и (17) имеют вид: и являются равномерно по n ограниченными. Для произвольной правой части получена оценка, устанавливающая устойчивость решения уравнения по правой части, из которой следует, чтоесли разностное уравнение (2) аппроксимирует исходное уравнение (1), то решение разностной задачи (2) сходится при τ → 0 к решению исходной задачи (1), причем порядок точности совпадает с порядком аппроксимации. Исследование устойчивости одношаговых и многошаговых блочных методов проводилось, как это принято, на модельном одномерном уравнении. Показано, что одношаговые блочные методы А-устойчивы и границей области устойчивости метода в комплексном пространстве является мнимая ось

Заключение

Блочные многошаговые многоточечные коллокационные методы, рассмотренные в статье, представляют обобщение известных многошаговых методов и существенно расширяют класс разностных методов решения задач Коши для обыкновенных дифференциальных уравнений. Проведенный анализ этих методов позволил получить оценки их устойчивости по Далквисту, сходимости по правой части и оценки погрешности. Полученные результаты представляют возможности построения новых более эффективных параллельных алгоритмов и их реализации на современных мультипроцессорных вычислительных системах. Проведенные численные решения одношаговыми блочными методами  тестовых жестких систем практически подтвердили их надежность и эффективность.

Литература

1. Дж. Холл, Дж. Уатт. Современные численные методы решения обыкновенных дифференциальных уравнений. - М.: Мир, 1979. – 312с.
2. Системы параллельной обработки. Под ред. Ивенса Д. М.: Мир,1985. – 416с.
3. Самарский А.А., Гулин А.В. Численные методы.- М.: Наука, 1989.- 432с.
4. Хайрер Э., Нёрсет С., Ваннер. Г. Решение обыкновенных дифференциальных уравнений. Нежесткие задачи. - М.: - Мир, 1990.-512с.
5. Хайрер Э., Ваннер. Г. Решение обыкновенных дифференциальных уравнений. Жесткие задачи. - М.: Мир, 1999.- 685с.
6. Молчанов И.Н. Введение в алгоритмы параллельных вычислений. АН УССР, Инст. Кибернетики им. В.М. Глушкова. Киев: Наукова думка. 1990. -128с.
7. Фельдман Л.П. Параллельные интерполяционные алгоритмы численного решения задачи Коши для обыкновенных дифференциальных уравнений на SIMD компьютере. Научн. Тр. ДонГТУ. Серия: Проблемы моделирования и автоматизации проектирования динамических систем, выпуск 10: - Донецк: ДонГТУ, 1999, с. 20-25.
8. Фельдман Л.П. Сходимость и оценка погрешности параллельных одношаговых блочных методов моделирования динамических систем с сосредоточенными параметрами. Научн. Тр. ДонГТУ. Серия: Iнформатика, Кiбернетика та обчислювальна технiка, выпуск 15: - Донецк: ДонГТУ,2000, с. 34-39.
9. Feldmann L.P. Implementierung und Effizienzanalyse von parallelen blockartigen Simulationsalgorithmen für dynamische Systeme mit konzentrierten Parametern. In: Möller, D.P.F. (Hrsg.): ASIM-Symposium Simulationstechnik in Hamburg, September 2000, SCS-Europe BVBA, Ghent/Belgium 2000, S. 241-246.
10. Фельдман Л.П., Дмитриева. О.А. Разработка и обоснование параллельных блочных методов решения обыкновенных дифференциальных уравнений на SIMD–структурах. Научн. Тр. ДонГТУ. Серия: Проблемы моделирования и автоматизации проектирования динамических систем, выпуск 29: - Донецк: ДонГТУ, 2001, с. 70-79.
11. Feldman L.P., Dmitrieva O.A., Gerber S.. Abbildung der blockartigen Algorithmen auf Parallelrechnerarchitekture. In: Tavangarian,D., Grützner, R. (Hrsg.): Tagungs-band 15. ASIM-Symposium Simulationstechnik in Rostock, September 2002, SCS-Europe BVBA, Ghent/Belgium 2002, S.359-364.
12. Фельдман Л.П. Параллельные алгоритмы моделирования динамических систем, описываемых обыкновенными дифференциальными уравнениями. //Электронное моделирование, том 26, № 1, 2004.- С. 19-30.
13. Фельдман Л.П., Назарова И.А. Параллельные алгоритмы численного решения задачи Коши для систем обыкновенных дифференциальных уравнений. //Математическое моделирование, том 18, №6, 2006. - С. 17-31.
14. Береговенко Г.Я., Пухов Г.Е., Саух С.Е. Численные операторные методы решения дифференциальных уравнений и анализа динамических систем. Киев, Наукова Думка, 1979. 162 с.