Щеглов Максим Игоревич

Факультет: Вычислительной техники и информатики
Специальность: Программное обеспечение автоматизированных систем
Тема магистерской диссертации: "Анализ и оценка эффективности параллельных многошаговых блочных методов решения ОДУ на кластере"
Научный руководитель: Фельдман Лев Петрович профессор, д.т.н.

Библиотека

Авторы: Щеглов М.І., Фельдман Л.П.

Донецкий национальный технический университет

Украина, 83001, Донецк, ул. Артема, 66.

АНАЛІЗ ТА ОЦІНКА ЕФЕКТИВНОСТІ ПАРАЛЕЛЬНИХ БЛОКОВИХ РІЗНИЦЕВИХ БАГАТОКРОКОВИХ МЕТОДІВ ЧИСЕЛЬНОГО РОЗВ’ЯЗАННЯ ЗАДАЧІ КОШІ

      Одним з найважливіших напрямків розвитку обчислювальних технологій є розпаралелювання обчислень. Але головною перешкодою на шляху розвитку паралелізму є відсутність паралельних алгоритмів. Доводиться шукати зовсім нові методи розв’язання різних задач. Досвід експлуатації сучасних високопродуктивних комп'ютерних систем показав, що ефективність їхнього застосування істотно залежить від узгодження структури паралельних обчислювальних систем з класом задач, що розв'язуються, і чисельних методів, які застосовуються. Ці обставини стали основою для адаптації відомих і пошуку нових методів розв’язання задачі Коші для звичайних диференційних рівнянь та систем звичайних диференційних рівнянь на паралельних системах. Тому тема даної роботи є актуальною задачею.
      Дослідження, викладені у докладі, присвячені розробці і аналізу ефективності паралельних блокових багатокрокових методів чисельного розв’язання задачі Коші. Багатокрокові методи розв’язування задачі Коші схильні для розпаралелювання, тому що в них відбувається обчислення одночасно кількох нових значень, тим самим підвищуючи швидкість обчислення. Також слід зазначити, що блокові методи досить актуальні, оскільки добре узгоджуються з архітектурою паралельних ОС і не вимагають обчислення значень у проміжних точках, що значно підвищує ефективність розрахунку.
      Рівняння багатокрокових блокових різницевих методів для блоку з k точок може бути записане у вигляді:

де f_n,0=f(t_n,0,u_n,0),i=1,k - номер точки

f_n,j=f(t_n+jτ,u_n,j),n=1,2,...

Для визначення коефіцієнтів a_i,j і b_i,j потрібно побудувати інтерполяційний багаточлен Лагранжа Lk(t) з вузлами інтерполяції tn,i ,i= 0,1,…,k і відповідними їм значеннями Fn,i=f(tn,i, un,i). Далі потрібно проінтегрувати його в межах (tn, tn+iτ), i=1,k

У підсумку одержимо формули, які шукаємо.
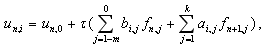
      Закріпимо кожений процесорний елемент за точкою n-го блоку, що розраховується. Тоді кожний з k процесорів спочатку буде обчислювати значення початкового вектора за методом Адамса-Башфорта.
      Далі кожен процесорний елемент буде знаходити відповідні вектори зі значеннями правих частин f_n,j=f(t_n+jτ,u_n,j) . Після чого буде здійснюватися обмін між процесорними елементами для виконання подальших обчислень і потім за заданими формулами, наприклад, триточечного блокового методу, будуть визначатися значення вектора наближеного розв’язку. Якщо ж кількість процесорів буде меншою за розмірность блоку, то деякі процесорні елементи будуть послідовно виконувати розрахунок декількох точок блоку, що в остаточному підсумку збільшить загальний час обчислень.
      Для оцінки показників прискорення та ефективності m–шагового k–крокового методу, порівняємо його з послідовним m-кроковим методом Адамса-Башфорта вирішення задачі Коші. Прискорення параллельних багатокрокових методів можна знайти за формулою:

W(k)=T₁/T_k

Коеффіцієнт еффективності метода можна знайти за формулою:

E(k)=W_k/N_проц

Якщо враховувати тільки час обчислення правоі частини рівнянь, то прискорення k-крапкового багатокрокового параллельного метода дорівнює k:

W(k)=k

а ефективність

E(k)=1

При цьому характеристики паралелізму в системах з кільцевою структурою виявляються гіршими, ніж у системах з топологією гиперкуб і тор, що свідчить про сильний вплив часу обмінів даними між процесорами в паралельних обчислювальних структурах. Між часом обчислення правої частини й ефективністю існує пряма залежність: при збільшенні трудомісткості обчислення правих частин ефективність розглянутих методів підвищується. Також слід зазначити, що в зв’язку з тим, що число точок блоку пов'язане з числом використовуваних процесорів, при збільшенні числа точок в блоці зростає коефіцієнт прискорення та к зменшується коефіцієнт ефективності . Підсумовуючи отримані результати, можна зазначити, що блоковий багатокроковий різницевий метод рішення задачі Коші для ОДУ є більш ефективним, ніж послідовний метод Адамса-Мултона для рішення тієї ж самоі задачі. Подальші дослідження направлені на порівняння різноманітних паралельних блокових багатокрокових алгоритмів рішення задачі Коші, аналіз їх масштабованості.

Література

Фельдман Л.П. Блочные методы решения задачи Коши для обыкновенных дифференциальных уравнений / Сборник трудов конференции Моделирование-2006. – К., 2006. – С. 423-427.
Хайрер Э., Ваннер Г. Решение обыкновенных дифференциальных уравнений. Жесткие и дифференциально-алгебраические задачи. – М.: Мир,1999. – 685с.