
Щеглов Максим Игоревич
Факультет: Вычислительной техники и информатики
Специальность: Программное обеспечение автоматизированных систем
Тема магистерской диссертации: "Анализ и оценка эффективности параллельных многошаговых блочных методов решения ОДУ на кластере"
Научный руководитель: Фельдман Лев Петрович профессор, д.т.н.
Библиотека
Авторы: Khairil Iskandar Othman, Zarina Bibi Ibrahim, and Mohamed Suleiman.
Перевод: М.И. Щеглов
Донецкий национальный технический университет
Украина, 83001, Донецк, ул. Артема, 66.
Параллельные блочные методы, использующие формулы обратного дифференцирования
Рассмотрим блочные методы, предложенные Zarina Bibi Bt Ibrahim, основанные на формулах обратного дифференцирования(Block Backward Differentiation Formulas - BBDF). Обычно BDF вычисляет приближение yn+1 для y(xn+1) на одном шаге, в то время как в 2-точечный BBDF, приближение решения yn+1 и yn+2 получаются одновременно на каждом шаге. Одновременная последовательность вычислений обозначается PECE. Аппроксимация первой точки:
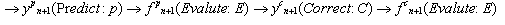 (2.1)
(2.1)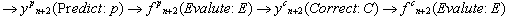 (2.2)
(2.2)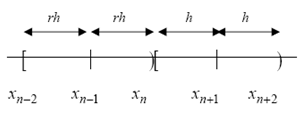
Рисунок 1.1 – Двухточечный метод BBDF
Пусть шаг h, для вычисляемого блока будет 2h и размер шага для предыдущего блока будет 2rh. Метод, в котором используются BBDF(Блочные формулы обратного дифференцирования) в общем виде записывается как
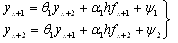 (2.3)
(2.3)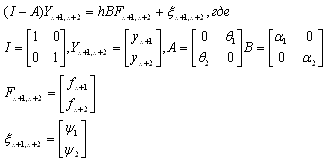

 и получим
и получим  , путем применения метода Ньютона для системы (2.3):
, путем применения метода Ньютона для системы (2.3):
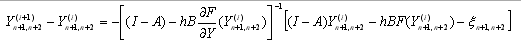 (2.4)
(2.4)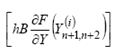


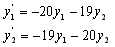
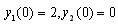

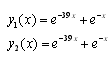

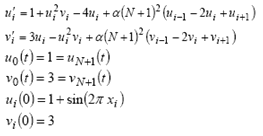

TOL : Tolerance used
TS : Всего шагов
FA : Общее количество отклоненных шагов
IST : Общее количество принятых шагов
MAXE : Максимальная погрешность полученного решения
BDF : Формулы обратного дифференцирования
BBDF : Блочные формулы обратного дифференцирования
S p : Ускорение
E p : Эффективность
EQN : Число вычислений
TIME : Время вычислений в сек.
В таблицах 2.1 и 2.2 приведены результаты, полученные при решении задач 1 и 2.
Таблица 2.1 Результаты решения задачи 1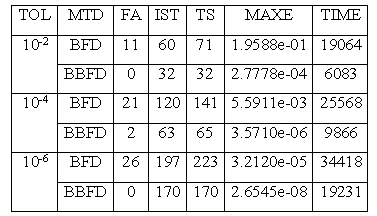

Таблица 3.2 Результаты решения задачи 2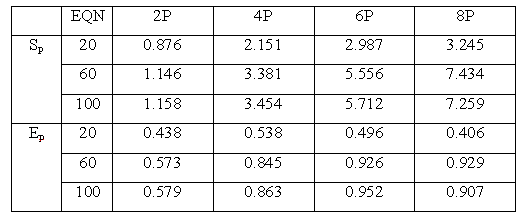
Численные результаты показывают, что ускорение возрастает с увеличением размерности решаемой задачи. В действительности, данная зависимость является линейной. Таким образом, использование параллельной реализация BBDF(Блочных формул обратного дифференцирования) является преимущественным по сравнению с использованием последовательных BDF.

Литература
- Khairil Iskandar Othman, Zarina Bibi Ibrahim, and Mohamed Suleiman - “Parallel Block Backward Differentiation Formulas for Solving Ordinary Differential Equations”, proceedings of world academy of science, engineering and technology volume 30 july 2008 issn 1307-6884