
Introduction
This document describes the Discrete Fourier Transform (DFT), that is, a Fourier Transform as applied to a discrete complex valued series. The mathematics will be given and source code (written in the C programming language) is provided in the appendices.
TheoryContinuous
For a continuous function of one variable f(t), the Fourier Transform F(f) will be defined as:

and the inverse transform as
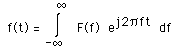
where j is the square root of -1 and e denotes the natural exponent

Discrete
Consider a complex series x(k) with N samples of the form
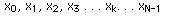
where x is a complex number

Further, assume that that the series outside the range 0, N-1 is extended N-periodic, that is, xk = xk+N for all k. The FT of this series will be denoted X(k), it will also have N samples. The forward transform will be defined as
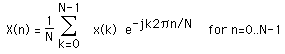
The inverse transform will be defined as
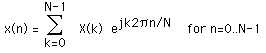
Of course although the functions here are described as complex series, real valued series can be represented by setting the imaginary part to 0. In general, the transform into the frequency domain will be a complex valued function, that is, with magnitude and phase.
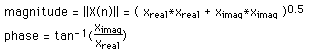
The following diagrams show the relationship between the series index and the frequency domain sample index. Note the functions here are only diagramatic, in general they are both complex valued series.

For example if the series represents a time sequence of length T then the following illustrates the values in the frequency domain.

Notes
The first sample X(0) of the transformed series is the DC component, more commonly known as the average of the input series.
The DFT of a real series, ie: imaginary part of x(k) = 0, results in a symmetric series about the Nyquist frequency. The negative frequency samples are also the inverse of the positive frequency samples.
The highest positive (or negative) frequency sample is called the Nyquist frequency. This is the highest frequency component that should exist in the input series for the DFT to yield "uncorrupted" results. More specifically if there are no frequencies above Nyquist the original signal can be exactly reconstructed from the samples.

Sample transform pairs and relationships
Applying the DFT twice results in a scaled, time reversed version of the original series.
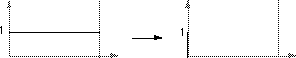



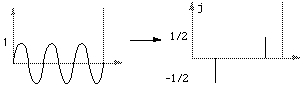

More precisely, if f(t) = 1 for |t| < 0.5, and f(t) = 0 otherwise then F(f) = sin(pi f) / (pi f)
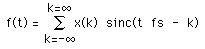
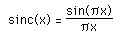
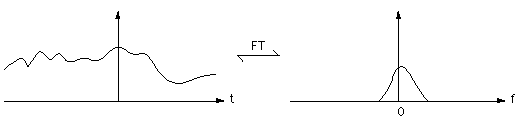
Consider a continuous signal in the time and frequency domain.

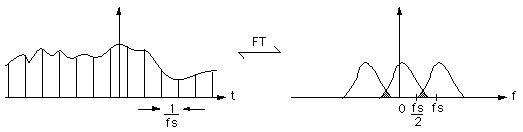
If the sampling frequency is too low the frequency spectrum overlaps, and become corrupted.
Appendix A. DFT (Discrete Fourier Transform)
/*
Direct fourier transform
*/
int DFT(int dir,int m,double *x1,double *y1)
{
long i,k;
double arg;
double cosarg,sinarg;
double *x2=NULL,*y2=NULL;
x2 = malloc(m*sizeof(double));
y2 = malloc(m*sizeof(double));
if (x2 == NULL || y2 == NULL)
return(FALSE);
for (i=0;i<m;i++) {
x2[i] = 0;
y2[i] = 0;
arg = - dir * 2.0 * 3.141592654 * (double)i / (double)m;
for (k=0;k<m;k++) {
cosarg = cos(k * arg);
sinarg = sin(k * arg);
x2[i] += (x1[k] * cosarg - y1[k] * sinarg);
y2[i] += (x1[k] * sinarg + y1[k] * cosarg);
}
}
/* Copy the data back */
if (dir == 1) {
for (i=0;i<m;i++) {
x1[i] = x2[i] / (double)m;
y1[i] = y2[i] / (double)m;
}
} else {
for (i=0;i<m;i++) {
x1[i] = x2[i];
y1[i] = y2[i];
}
}
free(x2);
free(y2);
return(TRUE);
}Appendix B. FFT (Fast Fourier Transform)
/*
This computes an in-place complex-to-complex FFT
x and y are the real and imaginary arrays of 2^m points.
dir = 1 gives forward transform
dir = -1 gives reverse transform
*/
short FFT(short int dir,long m,double *x,double *y)
{
long n,i,i1,j,k,i2,l,l1,l2;
double c1,c2,tx,ty,t1,t2,u1,u2,z;
/* Calculate the number of points */
n = 1;
for (i=0;i<m;i++)
n *= 2;
/* Do the bit reversal */
i2 = n >> 1;
j = 0;
for (i=0;i<n-1;i++) {
if (i < j) {
tx = x[i];
ty = y[i];
x[i] = x[j];
y[i] = y[j];
x[j] = tx;
y[j] = ty;
}
k = i2;
while (k <= j) {
j -= k;
k >>= 1;
}
j += k;
}
/* Compute the FFT */
c1 = -1.0;
c2 = 0.0;
l2 = 1;
for (l=0;l<m;l++) {
l1 = l2;
l2 <<= 1;
u1 = 1.0;
u2 = 0.0;
for (j=0;j<l1;j++) {
for (i=j;i<n;i+=l2) {
i1 = i + l1;
t1 = u1 * x[i1] - u2 * y[i1];
t2 = u1 * y[i1] + u2 * x[i1];
x[i1] = x[i] - t1;
y[i1] = y[i] - t2;
x[i] += t1;
y[i] += t2;
}
z = u1 * c1 - u2 * c2;
u2 = u1 * c2 + u2 * c1;
u1 = z;
}
c2 = sqrt((1.0 - c1) / 2.0);
if (dir == 1)
c2 = -c2;
c1 = sqrt((1.0 + c1) / 2.0);
}
/* Scaling for forward transform */
if (dir == 1) {
for (i=0;i<n;i++) {
x[i] /= n;
y[i] /= n;
}
}
return(TRUE);
}
Modification by Peter Cusack that uses the MS complex type fft_ms.c.
References
Fast Fourier Transforms
Walker, J.S.
CRC Press. 1996
Fast Fourier Transforms: Algorithms
Elliot, D.F. and Rao,
K.R.
Academic Press, New York, 1982
Fast Fourier Transforms and Convolution Algorithms
Nussbaumer,
H.J.
Springer, New York, 1982
Digital Signal Processing
Oppenheimer, A.V. and Shaffer,
R.W.
Prentice-Hall, Englewood Cliffs, NJ, 1975