Смоляная Д.В. - Перевод статьи Fast Fourier Transforming

Перевод статьи из свободной библиотеки Википедия.

Автор: Смоляная Дарья Владимировна.

Источних находится по адресу http://en.wikipedia.org/wiki/Fast_Fourier_transform

Быстрое преобразование Фурье

Материал из Википедии, свободной энциклопедии

Быстрое преобразование Фурье (FFT) представляет собой эффективный алгоритм для вычисления дискретного преобразования Фурье (ДПФ) и обратного ДПФ. Есть много различных алгоритмов БПФ, в которых применяется широкий спектр областей математики, от простой комплексно-численной арифметики до теории групп и теории чисел; в этой статье делается обзор имеющихся методов и некоторых их общих свойств, а уже конкретные алгоритмы описаны во вспомогательных статьях.

ДПФ раскладывает последовательности значений на компоненты различных частот.

Эта операция является полезной во многих областях (для ознакомления со свойствами и примерами применения см. дискретное преобразование Фурье), но расчет преобразования непосредственно по формулам, очень часто слишком медленый для практического применения.

БПФ это способ получить тот же результат, но значительно быстрее: расчет ДПФ из N точек непосредственно по формулам, занимает O (N ²⁾ арифметических операций, тогда как БПФ можно вычислить и получить тот же результат, но уже за O (N log N) операций.

Разница в скорости расчетов может быть существенной, особенно при больших объемах данных, где N, на практике, может достигать порядка тысячи или миллиона, и время вычисления может быть сокращено, в таких случаях, на несколько порядков. Уровень ускорения расчетов приблизительно пропорционален N / LOG (N).

Это огромное ускорение делает ДПФ приемлемым алгоритмом для применения его на практике; алгоритмы, которые реализуют БПФ имеют большое значение для широкого спектра приложений, от цифровой обработки сигналов и решения дифференциальных уравнений в частных производных до алгоритмов быстрого перемножения больших чисел.

Наиболее известны алгоритмы БПФ зависящие от факторизации N, однако (в отличие от популярных заблуждение) есть алгоритмы БПФ со сложностью вычисления равной O (N log N) для всех N, даже для натуральных N.

Многие алгоритмы БПФ зависят только от того, что $E ^ (- (2 \ Pi I \ над N))$ является примитивным корнем единицы. И, таким образом, могут применяться к аналогичным трансформациям для каких-либо конечных полей, таких, как теоретико-числовых преобразований.

С другой стороны обратное ДПФ это такая же трансформация, как и прямое ДПФ, но с обратным знаком в экспоненте, и дополнительный множитель равный 1 / N из любого алгоритма БПФ может легко сделать его обратную формулу.

Определение и скорость

БПФ вычисляет ДПФ и дает точно такой же результат, как и расчет ДПФ по его стандартным формулам напрямую; единственное различие заключается в том, что БПФ значительно быстрее.

Пусть х _0,… х_N_-1 будут комплексными числами. ДПФ определяется по формуле

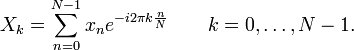
$X_k = \ sum_ (N = 0) ^ (N-1) x_n E ^ (- (I 2 \ Pi K \ Frac (N) (N))) \ qquad K = 0, \ точками, N-1.$

Непосредственная обработка этой формулы требует O (N ²⁾ операций: тут N выходящих значений X _K_, и каждое требует расчета суммы N выражении. В тоже врямя БПФ можно считать любой метод, который дает те же результаты , но за O (N log N) операций. Точнее, все известные алгоритмы БПФ требует Θ (N log N) операций (технически, O обозначает лишь верхнюю границу), хотя нет никаких доказательств того, что невозможно достичь меньшей сложности.

Для иллюстрации экономии на БПФ, рассмотрим вопрос о количестве умножений и сложений. Расчет ДПФ непосредственно связан с N ² комплексных операций умножения и N (N - 1) комплексных операций сложения [из которых O (N) операций может быть сохранена путем устранения тривиальных операций, таких как умножение на 1].

Известный БПФ алгоритм Кули-Тьюки, для всех N, которые являются степенью 2, можно получить тот же результат уже с (N / 2)log₂ N комплексными умножениями (опять же, игнорируя упрощенные умножения на 1, и т.п.) и N log₂ N комплексных сложений.

На практике же, фактическая производительность на современных компьютерах, как правило, зависит от других факторов, помимо арифметики, и это является непростой темой (см., например, Фриго и Джонсон, 2005), но общее улучшение от Θ (N ²) до Θ (N log N) все же остается необходимым.

Вычислительные вопросы

Границы от сложности и количество операций

Основополагающий вопрос и давний интерес для теоретиков заключается в том, чтобы доказать, нижние границы по сложности и найти точное количество операций для быстрого преобразования Фурье, и эти проблемы остаются открытыми. Не строго доказано даже то, а действительно ли ДПФ требуют $Ω$ $($ $N$ $log$ $N$ $)$ (то есть, порядка $N$ $logN$ или более) операции, даже для простого случая размеров равных степени двойки, хотя никаких алгоритмов с меньшими сложностями, как известно нет. В частности, количество арифметических операций, как правило, это центр внимания для вопросов подобного рода, хотя фактическая производительность на современных компьютерах, определяется также многими другими факторами, такими, как кэш-памяти и процессоры с поточной оптимизацией.

Следуя новаторской работе Винограда (1978), $Θ$ $(Н)$ нижняя граница известна для количества реальных умножений требующихся для БПФ. Может быть доказано, что только $4N-2 \ log_2 ^ 2) (N-2 \ log_2 N-4$ итеративных реальных умножений требуется выполнить для вычисления ДПФ для всех N, являющихся степенью двойки ( $N$ $= 2$ $m$ ).

Кроме того, явно известны алгоритмы для достижения этой цели (Heideman И Burrus, 1986; Duhamel, 1990). К сожалению, эти алгоритмы требуют слишком много сложений, что бы быть пригодными на практике, по крайней мере, на современных компьютерах с аппаратными умножителями. Жесткая нижняя граница не дает представления о количестве необходимых сложений, хотя нижние оценки были подтверждены в некоторых алгоритмах. В 1973 году Моргенштерн доказал $Ω$ $($ $N$ $log$ $N$ $),$ $как$ границу снизу, на основе алгоритмов, где множительные константы имеют ограниченные величины (что верно для большинства, но не для всех алгоритмов БПФ).Для случая «N – это степень двойки» $,$ Papadimitriou (1979) утверждал, что количество $N$ $log$ $2$ $N$ сложений комплексных чисел, которых достигли в алгоритме Кули-Тьюки , является оптимальным при определенных предположениях о графе этого алгоритма (его допущения предполагают, среди прочего, что ни одно сложение в корнях единицы не используется). (Этот аргумент предполагает, что требуется, по меньшей мере, $2$ $N$ $log$ $2$ $N$ реальных сложений, хотя это и не является жестким ограничением, поскольку дополнительные сложения требуется как часть умножений комплексных чисел.) До сих пор нет опубликованного алгоритма БПФ, который добивался бы меньше $N$ $log$ $2$ $N$ комплекснозначного числа сложений (или их эквивалент) для всех $N$ $,$ $которые являются степенью двойки .$

Третья проблема заключается в том, чтобы свести к минимуму общее число вещественных умножений и сложений, иногда называемых "арифметической сложностью" (хотя в данном контексте это выражение является точным и не подразумевает асимптотической сложности, которая в настоящее время и рассматривается). Повторюсь, не было доказано ни одной жесткой нижней границы. Начиная с 1968 года, однако, минимальное опубликованное количество действий для всех N равных степеням двойки, было давно достигнуто на БПФ алгоритмах с разделенными системами счислений, которые требуют $4$ $N$ $log$ $2$ $N$ $- 6$ $N$ $+ 8$ реальных умножений и сложений для $N$ $>$ $1.$ Но и это было недавно сокращено до $\ SIM \ Frac (34) (9) N \ log_2 N$ (Джонсон и Фрайго, 2007; Ланди и Ван Баскирк, 2007). Большинство попыток снизить или доказать сложность алгоритма БПФ были сосредоточены на очередной проблеме по работе с комплексными данными, поскольку она является наиболее простой. Тем не менее, БПФ с комплексными данными имеют проблемы, настолько тесно связанные с другими алгоритмами, такими, как БПФ с вещественными данными, дискретное косинус-преобразования, дискретные преобразования Хартли, и так далее, что любое улучшение в одном из них сразу же приведет к улучшению положения и в другом.

Точность и аппроксимация

Все эти алгоритмы FFT обсуждаемые ниже вычисляют ДПФ . А некоторые "БПФ" алгоритмы были предложены, однако, для того, что бы вычислить ДПФ примерно, с ошибкой, которая может быть сколь угодно малой за счет увеличения числа расчетов. Такие алгоритмы направляют ошибку приближения на увеличения скорости и другие свойства. Например, алгоритм приближений БПФ Эдельмана и др. (1999) достигает нижней коммуникационной потребности в параллельных вычислениях с помощью специального метода быстрого умножения. А вейвлет базированный алгоритм приближенных вычислений БПФ по Го и Баррусу (1996) принимает разреженные данные более эффективно, чем это возможно с точным БПФ. Другой алгоритм приближенного вычисления подмножества ДПФ выдает их (Шентов и др.). Только алгоритм Эдельмана работает одинаково хорошо, как с разреженными, так и не разреженными данными, поскольку он основан на сжимаемости (уровне дефицита) матрицы Фурье, а не на сжимаемости (разряженных) данных.

Даже в "точных" БПФ алгоритмах имеются ошибки при конечной точности с использованием арифметики с плавающей точкой, но эти ошибки, как правило, весьма невелики, большинство алгоритмов БПФ, например Кули-Тьюки, имеют отличные численные свойства. Верхняя граница по относительной погрешности на алгоритме Кули-Тьюки O (ε log N), по сравнению с O (ε N ^{3 / 2)} для родной ДПФ формулой (Джентльман и Санде, 1966).