Оригинал доступен по адресу http://alglib.sources.ru/fft/fourier.php
Преобразование Фурье и его свойстваО преобразовании Фурье, его смысле, свойствах и применении написано много книг, поэтому здесь будут описаны только самые важные его характеристики. Эта статья - своего рода теоретическая выжимка, и для её понимания следует уже обладать базовыми знаниями в этой области. Она не является учебником по преобразованию Фурье (уже существуют такие учебники, написанные профессионалами своего дела). Скорее, эта статья поможет освежить в памяти уже полученные знания в этой области, а также поможет вспомнить полезные формулы, которые у многих людей быстро улетучиваются из головы (к этой группе отношусь и я :) ). Перед началом изложения хочу выразить благодарность Олегу Красноярову за присланное письмо, в котором были кратко рассмотрены альтернативные алгоритмы БПФ, менее известные, чем широко использующийся вариант. Практически полностью это письмо легло в основу подраздела Быстрое преобразование Фурье. Преобразование ФурьеИтак, преобразование Фурье бывает двух видов: дискретное и непрерывное. Непрерывное используется математиками в аналитических исследованиях, дискретное применяется во всех остальных случаях.
Непрерывное преобразование Фурье - преобразование, которое применяется к функции h(t), заданной на интервале
также существует обратное преобразование, которое позволяет по образу H(f) восстановить исходную функцию h(t):
Очевидно, что образ H(f) является комплексной функцией вещественного аргумента, но также и h(t) может принимать не только вещественные, но и комплексные значения. Применение преобразования Фурье является столь обширной темой, что этот вопрос не будет подниматься в этой статье. Можно только перечислить несколько областей: анализ сигналов, фильтрация, ускоренное вычисление корелляции и свертки, использование в алгоритмах быстрого умножения чисел, и во многих других случаях оно также находит свое применение. Свойства непрерывного преобразования ФурьеВ таблице ниже описана связь свойств прообраза h и образа H.
Следующая таблица показывает, как меняется образ при изменении прообраза. Пусть запись
Следующий набор свойств относится к операциям свертки и корелляции. Свертка функций g и h определяется, как
Дискретное преобразование ФурьеС непрерывным преобразованием Фурье удобно работать в теории, но на практике мы обычно имеем дело с дискретными данными. Очень часто у нас дано не аналитическое выражение преобразуемой функции, а лишь набор её значений на некоторой сетке (обычно на равномерной). В таком случае приходится делать допущение, что за пределами этой сетки функция равна нулю, и аппроксимировать интеграл интегральной суммой:
В случае равномерной сетки эта формула упрощается. Также на равномерной сетке обычно избавляются от шага, чтобы получить безразмерную формулу:
Обратное преобразование в таком случае будет иметь вид
При внимательном рассмотрении можно заметить, что индекс при Hn принимает N+1 значение, в то время как при hk - только N значений. Таким образом, как будто бы получается, что функция H содержит в себе больше информации, чем h. На самом деле это не так, поскольку значения H-N/2 и HN/2 совпадают. Определенное таким образом, дискретное преобразование Фурье сохраняет практически все свойства непрерывного (разумеется, с учетом перехода к дискретному множеству). Быстрое преобразование ФурьеСколько операций требуется на проведение дискретного преобразования Фурье? Посчитав по определению (N раз суммировать N слагаемых), получаем величину порядка N 2. Тем не менее, можно обойтись существенно меньшим числом операций. Наиболее популярным из алгоритмов ускоренного вычисления ДПФ является т.н. метод Cooley-Tukey, позволяющий вычислить ДПФ для числа отсчетов N = 2 k за время порядка Nlog2 N (отсюда и название - быстрое преобразование Фурье, БПФ). Этот способ чем-то неуловимо напоминает быструю сортировку. В ходе работы алгоритма также проводится рекурсивное разбиение массива чисел на два подмассива и сведение вычисления ДПФ от целого массива к вычислению ДПФ от подмассивов в отдельности. Изобретение БПФ привело к потрясающему всплеску популярности преобразования Фурье. Целый ряд важных задач раньше решался за время порядка N 2, но после проведения преобразования Фурье над исходными данными (за время порядка Nlog2 N) решается практически мгновенно. Преобразование Фурье лежит в основе цифровых корелляторов и методов свертки, активно используется при спектральном анализе (практически в чистом виде), применяется при работе с длинными числами. Широко распространено ошибочное мнение о том, что метод Cooley-Tukey - единственный существующий метод выполнения БПФ, а само БПФ существует только для случая N = 2 k. На самом деле это не так - существуют алгоритмы БПФ для любого числа отсчетов. В одномерном случае, рассмотренном в этой статье, метод Винограда позволяет решить задачу для простого числа отсчетов N. Этот же алгоритм может быть легко обобщен на случай, когда N является степенью произвольного простого числа (а не только двойки), а также на случай, когда число N является произведением степеней простых чисел - т.е. N является произвольным числом, чье разложение на простые множители нам известно. В двумерном случае можно использовать метод Нуссбаумера. Существуют и другие алгоритмы, как для одномерного, так и для двумерного случаев, но рассмотрение этих вопросов выходит за рамки статьи (мне рекомендовали следующий источник - Блейхут, "Быстрые алгоритмы цифровой обработки сигналов"). Как уже говорилось выше, существуют алгоритмы БПФ для произвольного числа отсчетов, но наиболее широкое распространение получил только алгоритм для случая N = 2 k, что является существенным ограничением. Почему же это произошло? Причина этого в том, что алгоритм, построенный по методу Cooley-Tukey, обладает рядом очень хороших технологических свойств. Структура алгоритма и его базовые операции не зависят от числа отсчетов (меняется только число прогонов базовой операции "бабочка"). Алгоритм легко распараллеливается с использованием базовой операции и конвееризуется, а также легко каскадируется (коэфициенты БПФ для 2N отсчетов могут быть легко получены преобразованием коэфициентов двух БПФ по N отсчетов, полученных "прореживанием" через один исходных 2N отсчетов). Алгоритм прост и компактен, не требует дополнительной оперативной памяти и допускает обработку данных "на месте". Существует целый ряд оптимизированных именно для этого алгоритма DSP-процессоров (это одновременно и причина, и следствие). Всё это и обусловило популярность в инженерно/программистской среде именно этого алгоритма, и, соответственно, выбора именно 2 k отсчетов при использовании БПФ. Правда, попутно это привело к незаслуженному забвению широкими массами альтернативных алгоритмов, некоторые из которых (что следует отметить) требуют меньше вещественных операций на один отсчет, чем алгоритм Cooley-Tukey. Например, мне доводилось читать описание алгоритма, который по этому показателю на 20-40% (в зависимости от числа отсчетов) превосходил алгоритм Cooley-Tukey. © Сергей Бочканов, Олег Краснояров |
 . В результате получается функция H(f):
. В результате получается функция H(f):
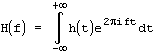
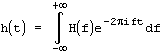
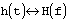 обозначает, что H(f) является образом h(t). Тогда имеют место следующие отношения:
обозначает, что H(f) является образом h(t). Тогда имеют место следующие отношения:



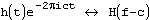
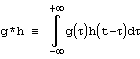 . Корелляция функций g и h определяется, как
. Корелляция функций g и h определяется, как 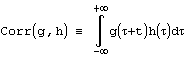 . В таком случае имеют место следующие отношения:
. В таком случае имеют место следующие отношения:
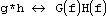
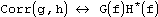
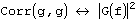
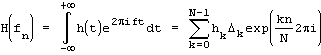
![H_n_ ≡ sum(h_k_exp(div(kn,N)2πi),k=0,N-1) n∈[-div(N,2),div(N,2)]](fourier_files/visualize_002.png)
![h_k_ ≡ div(1,N)sum(H_n_exp(-div(kn,N)2πi),n=0,N-1) k∈[0, N-1]](fourier_files/visualize_013.png)