Авторы: Станислав Огрызков, Иван Головинов и Павел Денисов, 26.12.2007

Исходный текст находится по адресу http://stanislaw.ru/rus/studies/imagine.asp?section=fourierdiscrete


Курсовая работа по обработке изображений

Настоящие методические указания предназначены, прежде всего, для студентов моей специальности 230101 «Вычислительные машины, комплексы, системы и сети», которые хотели бы успешно выполнить курсовую работу по дисциплине с громким названием «Обработка изображений, распознавание образов и мультимедиа». Также они могут быть полезны для студентов и других специальностей и вообще всех интересующихся обработкой изображений и распознаванием текста.

Дискретное преобразование Фурье 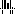Дискретное преобразование Фурье

Дискретным преобразованием Фурье (ДПФ) над исходной последовательностью чисел {x0, x1, …, xn-1} мощностью n є N, n>1, где xi є Z, i = (0, n-1), называется такое преобразование, в результате которого получается последовательность {x-0, x-1, …, x-n-1} комплексных чисел x-k той же мощности, каждый элемент которой рассчитывается по правилу:

Коэффициенты ДПФ

где k = (0, n-1), W = e-j*Пи/n, где j – мнимая единица.

Существуют такие Wik, у которых (ik) равны. Нетрудно заметить, что для выполнения n-точечного преобразования Фурье необходимо выполнить n (n-1) комплексных сложений и (n-1) (n-1) комплексных умножений (с учётом W0=1). При этом множитель Wik будет использован столько раз, сколько делителей из диапазона (0, n-1) у показателя степени (ik).

Имеем:

Тригонометрическое представление

Поскольку sin Альфа = – sin (Альфа + Пи), cos Альфа = – cos (Альфа + Пи), то

Связность по знакам (1)

откуда следует, что

Связность по индексам (2)

Таким образом, диапазон степеней (ik) с помощью формулы (1) мы сокращаем с (0, (n-1)(n-1)) до (0, n-1), а с помощью формулы (2) – до (0, n/2 - 1).

Пусть n – длина исходной последовательности чисел {x0, x1, …, xn-1} чётна, тогда преобразование Фурье для такой последовательности можно записать в виде:

Разложение на подсуммы (3)

С учётом формулы (1), а также выражения

Связность по индексам

формулу (3) часто записывают в виде:

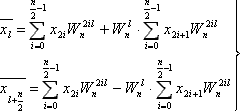Разложение на подсуммы (4)

Рассмотрим первую сумму формулы (3). Положив n / 2 = m, получим:

1) n = 2m;
2) Связность по индексам;
3) Связность подсумм.

Аналогичные рассуждения можно провести и в отношении второй суммы формулы (3). Таким образом, ДПФ исходной последовательности размерностью n=2m свелось к двум ДПФ последовательностей размерностью m чисел каждая, составленных из чётных и нечётных элементов исходной последовательности.

Быстрое преобразование Фурье (БПФ)

Формулы (3) и (4) являются основой для построения алгоритма быстрого преобразования Фурье (БПФ). Этот алгоритм за счёт рекурсивного применения формулы (3) сводит ДПФ исходной последовательности размерности n=2l, где l є N, к набору 2-точечных преобразований Фурье.

По определению имеем:

Коэффициенты ДПФ

Умножим x-k на Wn-jk и просуммируем по k = 0 .. (n-1):

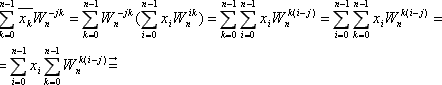
Вывод формулы обратного ДПФ

Можно доказать, что

Равенство суммы нулю

где a є Z, a>0, поэтому

Значение суммы

имеем:

Вывод формулы обратного ДПФ

– мы получили формулу для обратного ДПФ (ОДПФ):

Формула ОДПФ

откуда видно, что ОДПФ есть прямое ДПФ (ПДПФ) результата предыдущего ПДПФ, делённое на n.

Двумерное ДПФ – это ДПФ над матрицей:

Формула двумерного ДПФ

где k,i = (0, n-1), l,j = (0, m-1), то есть это есть последовательное одномерное ДПФ сначала над строками, а потом над строками.

Общий вид обратного двумерного ДПФ:

Формула обратного двумерного ДПФ

Практическая реализация

При практической реализации в качестве исходных данных для демонстрации работы алгоритмов ДПФ удобно использовать значения точек изображения, подвергающегося обработке другими алгоритмами. При этом под «значениями» точек понимается либо значения каждого из цветовых каналов, либо значение яркости (найденное по известной формуле), либо значение типа TColor элемента массива Pixels[], – это неважно. Важно то, что всё выполняется примерно по следующий схеме:

  1. Значения точек заносятся в область памяти, выделенную для действительных частей дискретов (речь ведь идёт о работе с комплексными числами).
  2. Область памяти, выделенная для мнимых частей дискретов, заполняется нулями (так как значения точек изображения – чисто действительные числа).
  3. Вызывается процедура необходимого преобразования Фурье (одномерное или двумерное БПФ), которой передаются указатели на выделенные области памяти и их размеры, а также направление преобразования (в данном случае прямое).
  4. В качестве наглядного представления коэффициентов, полученных после преобразования (в тех же областях памяти) используются модули комплексных чисел, которые делаются значениями соответствующих точек изображения.
  5. Сами области памяти сохраняются до выполнения обратного преобразования, так как они хранят комплексные значения коэффициентов (после прямого БПФ мнимые части отличны от нуля).
  6. При выполнении обратного преобразования той же универсальной процедуре передаются указатели на хранимые области памяти, их размеры и направление преобразования (обратное).
  7. Модули комплексных чисел, полученных после обратного БПФ, являются исходными значениями точек изображения, так как их мнимые части равны нулю.
  8. Освобождаются выделенные области памяти.

Пример процедуры для выполнения одномерного БПФ приведён ниже:

// (C) 1999 Иван Головинов
procedure LinearFDFT (Re, Im: PReal; Count: Word; Direct: ShortInt);
  var
    I: Word;
    K: Real;
    PIm, PRe: PReal;
  procedure LFDFT (SrcRe, SrcIm: PReal; Cnt: Word);
    var
      EvenRe, OddRe, PEvenRe, POddRe, PRe, PSrcRe: PReal; …;  // То же - для мнимых
      Factor: Real;
      HalfCnt, I, Size: Word;
      HEvenIm, HEvenRe, HOddIm, HOddRe: THandle;
      X, Y, WIm, WRe: Real;
    begin
      PSrcRe := SrcRe; …;
      if Cnt = 2 then
        begin // Тривиальная операция «бабочка»
          Inc (PSrcRe); …;
          X := SrcRe^; Y := PSrcRe^;
          SrcRe^ := X + Y; PSrcRe^ := X - Y;
          X := SrcIm^; Y := PSrcIm^;
          SrcIm^ := X + Y; PSrcIm^ := X - Y;
        end      
      else
        begin // Переупорядочение и рекурсивный вызов для полпоследовательностей
          Factor := K / Cnt;
          HalfCnt := Cnt div 2;
          Size := HalfCnt * SizeOfReal + 1;
          HEvenRe := GlobalAlloc (GMem_Fixed, Size); …;
          HOddRe := GlobalAlloc (GMem_Fixed, Size); …;
          EvenRe := GlobalLock (HEvenRe); …;
          OddRe := GlobalLock (HOddRe); …;
          PEvenRe := EvenRe; …;
          POddRe := OddRe; …;
          // Разбивка на (не)чётные подпоследовательности
          for I := 0 to Cnt - 1 do
            begin
              if Odd (I) then
                begin
                  POddRe^ := PSrcRe^; …;
                  Inc (POddRe); …;
                end
              else
                begin
                  PEvenRe^ := PSrcRe^; …;
                  Inc (PEvenRe); …;
                end;
              Inc (PSrcRe); …;
            end;
          // Рекурсивная обработка (не)чётных подпоследовательностей
          LFDFT (EvenRe, EvenIm, HalfCnt);
          LFDFT (OddRe, OddIm, HalfCnt);
          // Сборка обработанных подпоследовательностей
          PSrcRe := SrcRe; …;
          PRe := SrcRe; …;
          Inc (pRe, HalfCnt); …;
          PEvenRe := EvenRe; …;
          POddRe := OddRe; …;
          for I := 0 to HalfCnt - 1 do
            begin
              WRe := Cos (Factor * I); WIm := - Sin (Factor * I);
              PSrcRe^ := POddRe^ * WRe - POddIm^ * WIm;
              PSrcIm^ := POddRe^ * WIm + POddIm^ * WRe;
              PRe^ := pSrcRe^; …;
              PSrcRe^ := pEvenRe^ + PSrcRe^; …;
              PRe^ := PEvenRe^ - PRe^; …;
              Inc (PSrcRe); …;
              Inc (PRe); …;
              Inc (PEvenRe); …;
              Inc (POddRe); …;
            end;
          GlobalUnlock (HEvenRe); …;
          GlobalUnlock (HOddRe); …;
          GlobalFree (HEvenRe); …;
          GlobalFree (HOddRe); …;
        end;
    end;
  begin
    K := 2 * Pi * Direct;
    LFDFT (Re, Im, Count);
    if Direct < 0 then
      begin // Дополнительное деление на n для обратного преобразования
        PRe := Re; …;
        for I := 1 to Count do
          begin
            PRe^ := PRe^ / Count; …;
            Inc (PRe); …;
          end;
      end;
  end;

Оптимизация здесь может заключаться в использовании другого типа данных (константа SizeOfReal может быть заменена на выхов оператора SizeOf(Type) для конкретного типа Type), других способов выделения и освобождения памяти (например, с использованием функций GetMem и FreeMem) и т. п. В случае двумерного преобразования используется та же функция, но последовательно, сначала для строк, потом для столбцов (или наоборот).