Design of Finite State Machines

with Transformation of the Object’s Codes

 

Barkalov A.A., Institute of Informatics and Electronics. Zielenogorski University,  POLAND, Lavrik A.S., master degree student, DonNTU, Donetsk, Ukraine

 

 

Introduction

A control unit (CU) of any digital system can be represented as Mealy or Moore finite state machine (FSM). The minimization of hardware in the circuits of control units (CU) implemented on the Programmable Logic Devices (PLD) can be worked out thanks to the increasing of the number of levels in the circuit of FSM [1]. In this case optimization of the circuit that implements the microoperations of the digital  system is connected with formation of some additional variables [2, 3]. The method that permits to decrease the amount of additional variables and, therefore, an amount of PLDs in the circuit of FSM is proposed in this article.

 

 

The main definitions and an idea of the optimization's method

Let a control unit is represented as finite state machine S with set of  internal states , set of  logic conditions , set of microoperations  and terms  and let each term corresponds to one line of the direct structural table (DST ) [1]. Let DST has Z different sets of microoperations  and let states  are encoded using special set of  internal variables , where R = ]log₂M[. Let each set Y_z corresponds to the binary code K(Y_z) with Q = ]log₂Z[ bits and let these encoding variables form set . The states correspond to the binary codes K(a_m) with  R bits. Let’s name state  and set  as the objects of FSM S. The main idea of the proposed method is following.

One of the objects (state or set of microoperations) is a function on the terms of DST and second object is the function of the first one and - may be- some additional elements. Such approach is based on the insertion of special code transformer (CT) in the structure of FSM.  If code transformer CT  implements the matching, then we’ll name such FSM as PC_AY – FSM. If code transformer CT implements the matching, then we’ll name such FSM as PC_YY – FSM. The figures 1 and 2 show the structures of  PC_AY- FSM and PC_YY – FSM that are the Moore FSM. Here  W is the set of variables that are necessary for one-to-one identification of the objects [4].

 

Figure  1 – The structural circuit of  Moore PC_AY- FSM

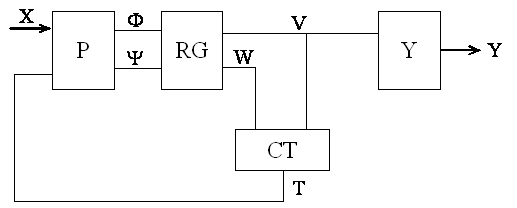
Figure  2 – The structural circuit of  Moore PC_YY-FSM

Because of the independence of the output functions of Moore FSM from the logic conditions, the subcircuit Y implementing the system of output functions Y can be connected with the outputs of register  RG whether  directly (PC_YY – FSM) or through the circuit CT (PC_AY – FSM). Here subcircuit  P  forms the excitation functions   and special functions  that are needed to form in the RG whether the functions T(PC_AY – FSM) or the functions  V and W (PC_YY – FSM). PC_AY – FSM does not form functions Y because of relation

 

             .                                                    (1)

 

Condition (1) is true only for particular case of Mealy FSM. It is the reason to form the functions W in  Mealy PC_AY- FSM (Fig.3) and PC_YY – FSM (Fig.4).

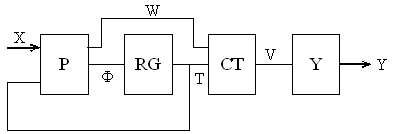
Figure  3 –  The structural circuit of Mealy  PC_AY-FSM

 

Figure  4 – The structural circuit of  Mealy  PC_YY-FSM

 

If codes of the objects are form by subcircuit P such objects are named as primary objects. If codes of the objects are the functions from other objects they are named as the secondary objects.

 

 

Common method of design of automata with transformation of objects

The method of design for any automaton includes the same steps:

1. Formation of the direct structural table of FSM. In this case an initial information about a control algorithm is represented as a flow-chart marked by the states of the corresponding FSM.

2. Determination of the set of variables I to the one-by-one identification of the secondary objects by primary ones [4].

The amount of the variables in the set I should be minimal one to decrease the total amount of the required outputs of the  subcircuit P.           

3. Encoding of the sets of microoperationsusing the elements of the set V. Formation of  table of microoperations. This step is executed for further design of the transformed DST. The amount of variables in the set V should be minimal to minimize the amount of outputs in the subcircuit  P.

4. Encoding of the variables  using the elements of the set, where  P = ]log₂K[. Such approach permits to minimize the total amount of outputs in the subcircuit P and the amount of the inputs in the code transformer.

5. One-to-one identification of the secondary objects by the codes of prime objects and codes  K(I_K) of variables .

6. Formation of the transformed DST by excluding of the column of secondary objects and insertion of the column of variables for identification.

7. Formation of the system of functions implemented by subcircuit P using the transformed DSP.

8. Formation of the table of code converter and the system of its functions.

9. Design of the logical circuit of FSM in the given base.

 

The examples of application of this procedure with details for design of particular structure of FSM can be found in literature [4,5].

 

 

Table 1- Initial DST of Moore FSM

 

Let us discuss an example of Moore FSM design using Table 1. This table contains  Т=4 sets of microoperations: Y₁=Æ, Y₂={y₁,y₂}, Y₃={y₃}, Y₄={y₃,y₄}, and  Q=2 variables is sufficient to encode them so  Z={z₁, z₂}.Let К(Y₁)=00, K(Y₂)=01, …, K(Y₄)=11. Then tables of microoperations and code transformer are given in the tables 2 and 3 respectively.

Functional circuit of FSM is shown on the figure 5. The application of this method is profitable if

         R > Q.                                                      (2)

 

Table  2 - Table of microoperations of Moore FSM

 

 

Table  3 - Table of the code transformer of Moore FSM

 

 

 

References

1.       Baranov S. Logic Synthesis of Control Automata– Kluwer Academic Publishers, 1994. – 312 pp.

2.       Скляров В.А. Синтез автоматов на матричных БИС – Минск: Наука и техника, 1984. – 287 с.

3.       Соловьёв В.В Проектирование цифровых систем на основе программируемых логических интегральных схем. – М.: Горячая линия – Телеком, 2001. – 636 с.

4.       Баркалов А.А., Баркалов А.А. Оптимизация схем автоматов Мура с кодированием наборов микроопераций / В кн. “Автоматизация проектирования дискретных систем”. Материалы 4-й Международной конференции (14-16.11.2001, Минск). Том 2. – Минск: ИТК НАН Беларуси, 2001. – C.14-19.

5.       Баркалов А.А., Палагин А.В. Синтез микропрограммных устройств управления.– Киев: ИК НАН Украины, 1997. – 135 с.

    6. Баркалов А.А. Принцип оптимизации логической схемы микро-программного автомата Мура // Кибернетика и системный анализ. – 1998. - №1. – C. 65-72.

    7. Баркалов А.А., Зеленева И.Я. Оптимизация логической схемы устройства управления с заменой переменных // Управляющие системы и машины. – 2001. - №1.– C.75-78.