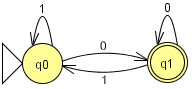
Рисунок 1. Простой детерминированный конечный автомат.
Источник: http://www.rsdn.ru/article/alg/nka.xml
| Просто конечные автоматы Добавляем недетерминированность … и эпсилон-переходы И почему это круто Реализация методом «в лоб» Реализация преобразованием в ДКА Заключение |
Подвёл ты меня, Боролгин. А ведь я все деньги на тебя поставил. .. <тут Боролгин сокрушается> .. Не горюй, Боролгин. Я ещё и на орков поставил. Арагорн в переводе Гоблина
Недетерминированные конечные автоматы – одна из моделей, используемых в теории вычислений. Вряд ли всё это когда-нибудь пригодится вам «по жизни»… но, чёрт возьми, математика – это интересно! Во всяком случае, для меня. А если уж она хоть как-то с программированием связана, то интересна вдвойне.
Я не претендую на математическую строгость, получилось что-то типа «популярной математики для чайников»… Но надо же с чего-то начинать. А причём здесь орки – поймёте по ходу дела :)
Скорее всего, все более-менее знают, что такое конечные автоматы. Проблема в том, что я, например, знаю три варианта: конечные автоматы Мура, конечные автоматы Мили и «просто» конечные автоматы. Поскольку дальше нам потребуется вполне конкретное определение, имеет смысл ввести его здесь.
Итак, детерминированным конечным автоматом (ДКА) называется устройство, описываемое следующими параметрами:
И функционирующие следующим образом:
| ПРИМЕЧАНИЕ Возможно, более простым вам покажется следующее определение: детерминированным конечным автоматом называется такой автомат, в котором при любой данной последовательности входных символов существует лишь одно состояние, в которое автомат может перейти из текущего. – прим.ред. |
Работа ДКА заключается в распознавании цепочек символов, принадлежащих множеству Σ. Если, обработав цепочку, автомат оказался в допускающем состоянии, то цепочка считается допустимой, если нет, то нет. Таким образом, ДКА задаёт некоторый язык – множество допускаемых им цепочек, алфавит этого языка – множество Σ.
| ПРИМЕЧАНИЕ Это определение конечного автомата используется в теории вычислений. Автоматы Мура и Мили используются, в основном, при проектировании цифровой аппаратуры. |
Конечные автоматы удобно изображать графически. На рисунке 1 приведён несложный ДКА, допускающий цепочки из 0 и 1, заканчивающиеся символом 0. Начальное состояние помечено входящей в него стрелочкой (да, этот здоровенный треугольник в душе – стрелочка), допускающее (в данном случае оно одно) – двойным кружком.

Рисунок 1. Простой детерминированный конечный автомат.
Второй вариант изображения автоматов – таблица переходов.
| 0 | 1 | ||
|---|---|---|---|
| -> | q0 | q1 | q0 |
| * | q1 | q1 | q0 |
По горизонтали отложены символы входного алфавита, по вертикали – состояния, начальное состояние отмечено стрелочкой, а допускающие – звёздочками. Этот способ изображения менее нагляден, и приведён только в качестве примера, использовать его «для дела» я не буду.
Определение недетерминированного конечного автомата (НКА) практически полностью повторяет приведённое выше определение ДКА. Отличий всего два:
НКА тоже распознаёт цепочки символов, цепочка считается допустимой, если после её обработки множество состояний, в котором оказался автомат, содержит хотя бы одно допускающее. Таким образом, НКА также задаёт некоторый язык.
На рисунке 2 изображён простой НКА, допускающий цепочки из 0 и 1, заканчивающиеся на 00.
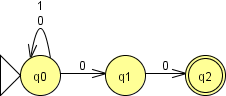
Рисунок 2. Простой недетерминированный конечный автомат.
Этот же автомат в виде таблицы:
| 0 | 1 | ||
|---|---|---|---|
| -> | q0 | {q0, q1} | {q0} |
| q1 | {q2} | Ø | |
| * | q2 | Ø | Ø |
Разберёмся, как он работает.
Допустим, на вход автомату поступила цепочка «100100».
| До | Вход | Описание | После |
|---|---|---|---|
| Автомат начинает работу в множестве состояний {q0} | {q0} | ||
| {q0} | 1 | Из состояния q0 по символу 1 существует только один переход, в q0 же. | {q0} |
| {q0} | 0 | Из состояния q0 по символу 0 существует два перехода, в q0 и в q1. | {q0, q1} |
| {q0, q1} | 0 | Из состояния q0 по символу 0 существует два перехода, в q0 и в q1, из состояния q1 – один переход, в q2. Поскольку автомат находится в двух состояниях, множества объединяются. | {q0, q1, q2} |
| {q0, q1, q2} | 1 | Автомат находится в трёх состояниях, но из q1 и из q2 не существует переходов по символу 1 (т.е. значение функции перехода из этих состояний по входному символу 1 – пустое множество). В итоге остаётся только q0. | {q0} |
| {q0} | 0 | И т.д. | {q0, q1} |
| {q0, q1} | 0 | И т.п. Так как в получившемся множестве состояний есть q2 – допускающее состояние, автомат признаёт цепочку корректной. | {q0, q1, q2} |