Источник: http://www.chipinfo.ru/literature/chipnews/200209/1.html

В. Соловьев

Структурные модели конечных автоматов при их реализации на ПЛИС

Конечный автомат представляет собой наиболее общую математическую модель цифрового устройства или цифровой системы. Поэтому очень важно при разработке различных цифровых устройств и систем применять эффективные методы синтеза конечных автоматов. В то же время, реализованные в известных пакетах автоматизированного проектирования (фирм Altera, Xilinx и других) методы синтеза основаны на традиционных подходах, которые не позволяют эффективно использовать архитектурные возможности новой элементной базы.Данная статья является первой из серии статей, посвящённых новому подходу к синтезу конечных автоматов на ПЛИС. В рамках данной серии предполагается опубликовать следующие статьи: "Проектирование конечных автоматов на ПЛИС со структурой двух программируемых матриц"; "Использование выходных макроячеек ПЛИС в качестве элементов памяти конечных автоматов"; "Использование входных буферов ПЛИС в качестве элементов памяти конечных автоматов"; "Синтез на ПЛИС совмещённых моделей конечных автоматов"; "Верификация результатов синтеза конечных автоматов на ПЛИС"; "Пакет ZUBR автоматизированного проектирования конечных автоматов на ПЛИС".В статьях данной серии будут рассмотрены формальные методы синтеза конечных автоматов на ПЛИС, которые позволяют наиболее полно и эффективно использовать архитектурные возможности ПЛИС. Отличительной чертой всех методов синтеза является простота, что делает возможным их применение даже при ручном проектировании.Экспериментальные исследования показали, что предлагаемый подход позволяет сократить стоимость реализации и повысить быстродействие конечных автоматов, в среднем, в 2–3 раза, по сравнению с известными пакетами.

В настоящее время хорошо исследованы две модели автоматов: автомат Мили [1] и автомат Мура [2]. Известна также модель автомата [3,4], в которой наборы выходных сигналов совпадают с кодами внутренних состояний автомата. В отдельных работах предлагается использовать регистры на входах и выходах автомата для буферизации входных сигналов и согласования выходных сигналов с сигналами синхронизации [5].

Однако до сих пор не исследованы все возможные модели конечных автоматов, допускающих реализацию на современных программируемых логиче-ских интегральных схемах (ПЛИС), влияние установки регистров на входах и выходах на поведение автомата, во-просы временного согласования сигналов автоматов при передаче значений между различными уровнями в многоуровневых цифровых системах с различными способами обработки данных, не определена сложность реализации на ПЛИС различных моделей конечных автоматов и др. Указанные проблемы становятся особенно острыми, когда необходимо достичь максимального быстродействия устройства, приближающегося к предельной частоте функционирования ПЛИС.

В данной работе рассматриваются различные структурные модели конечных автоматов, допускающие реализацию на ПЛИС. Для этого вводятся различные классы конечных автоматов, на основании которых определяются структурные модели конечных автоматов, реализуемых на ПЛИС. Основной целью исследования является выявление свойств каждой модели с точки зрения быстродействия и стоимости реализации.

Классы конечных автоматов

На практике наибольшее распространение получили два типа конечных автоматов: автомат Мили и автомат Мура. Поведение автомата Мили описывается с помощью следующих уравнений:

a_t+1 = (z_t,a_t); (1)
w_t = (z_t,a_t);

здесь функция переходов определяет следующее внутреннее состояние автомата (состояние перехода) a_t+1, а функция выходов - формируемый выходной набор w_t. Характерным для автомата Мили является то, что выходной набор wt зависит как от входного набора zt, так и от внутреннего состояния a_t

В автомате Мура функция выходов зависит только от состояния a_t и не зависит от входного набора, поэтому поведение автомата Мура описывается следующими уравнениями:

a_t+1 = (z_t,a_t); (2)
w_t = (a_t).

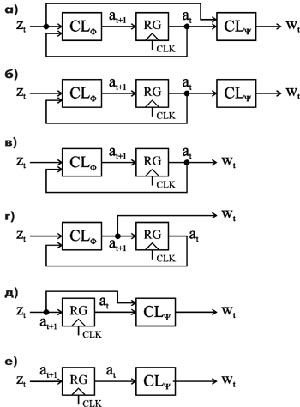
При построении конечных автоматов функции переходов и выходов реализуются с помощью комбинационных схем CL и CL, соответственно, а память автомата реализуется в виде регистра RG, где в каждый момент автоматного времени t~ хранится код внутреннего состояния a_t. Структурные схемы автоматов Мили и Мура показаны на рис. 1а и 1б, соответственно. Особенностью структуры автомата Мура является то, что комбинационная схема CLy, реализующая выходные функции, не имеет непосредственной связи со входами схемы.

Рисунок 1. Основные структуры конечных автоматов: а - Мили класса A; б - Мура класса B; в - Мура класса С; г - Мили класса D; д - Мили класса E; е - Мура класса F;

Если каждый выходной набор w_t автомата Мура совпадает с кодом его внутреннего состояния a_t, то поведение автомата можно описать следующим образом:

~a_t+1 = (z_t,a_t); (3)
w_t = a_t.

Данный тип автомата называют автоматом класса C [6], аналогично, автоматы Мили (рис. 1а) и Мура (рис. 1б) называют автоматами классов A и B, соответственно. Структура автомата Мура класса C показана на рис. 1в. Её особенностью является отсутствие комбинационной схемы CL, а также то, что все выходы автомата являются регистровыми, поскольку формируются на выходах регистра RG. Отметим, что данная структура легко реализуется на ПЛИС, поскольку все регистровые выходы имеют цепи обратной связи с комбинационной частью ПЛИС.

Если каждый выходной набор w_t автомата Мили совпадает с кодом его состояния перехода a_t+1, то имеем автомат класса D [7], поведение которого описывается следующими уравнениями:

~ a_t+1 = (z_t,a_t); (4)
w_t = a_t+1.

Структура автомата Мили класса D показана на рис. 1г. Её особенностью также является отсутствие комбинационной схемы CL, однако выходы автомата являются комбинационными, поскольку формируются на выходах комбинационной схемы CL . Отметим, что необходимым условием реализации автоматов класса D на ПЛИС является возможность такого конфигурирования выходных макроячеек, при котором триггеры выходных макроячеек включены в цепи обратных связей.

Различие между автоматами классов C и D заключается в том, что в автомате класса C выходной набор w_t совпадает с кодом настоящего внутреннего состояния a_t, а в автомате класса D выходной набор w_t определяет код следующего состояния a_t+1 (состояния перехода). Преимущество автоматов классов C и D, по сравнению с автоматами классов A и B, заключается в следующем:

• упрощается комбинационная часть автомата, поскольку отпадает необходимость в реализации комбинационной схемы CL, и
• уменьшается число используемых выходных макроячеек, так как память автомата и выходные функции реализуются на одних и тех же макроячейках ПЛИС.

Коды внутренних состояний конечного автомата могут определяться не только наборами значений выходных переменных, но также и наборами значений входных переменных [8]. Если каждый входной набор z_t автомата Мили совпадает с кодом следующего состояния a_t+1, то имеем автомат класса E, уравнения функционирования которого имеют вид:

a_t+1 = z_t; (5)
w_t = (z_t,a_t).

Аналогично, если каждый входной набор z_t автомата Мура совпадает с кодом следующего состояния a_t+1, то имеем автомат класса F, поведение которого можно описать следующим образом:

a_t+1 = z_t; (6)
w_t = (a_t).

Особенностью структур автоматов классов E (рис. 1д) и F (рис. 1е) является отсутствие комбинационной схемы CL. В автомате класса E комбинационная схема CL имеет два типа входов: прямые (комбинационные) и буферизированные (регистровые), а в автомате класса F - только один тип входов: буферизированные.

Необходимым условием реализации на ПЛИС автоматов классов E и F является возможность буферизации в регистрах входных сигналов. Кроме того, для построения автомата класса E входы ПЛИС должны иметь два типа связи с комбинационной частью ПЛИС: прямую и буферизированную. Буферизация входных сигналов для различных ПЛИС может осуществляться с помощью: ячеек ввода/вывода, скрытых макроячеек, выходных макроячеек и др. Для определённости любые макроячейки ПЛИС, используемые для буферизации входных сигналов, будем называть входными макроячейками ПЛИС.

Преимущество автоматов классов E и F, по сравнению с автоматами классов A и B, заключается в следующем:

• упрощается комбинационная часть автомата, поскольку отпадает необходимость в реализации комбинационной схемы CL, и
• сокращается число используемых скрытых (либо выходных, если скрытые отсутствуют) макроячеек, так как память автомата реализуется с помощью входных буферов ПЛИС.

Существенным различием между автоматами Мура классов C и F является то, что в автомате класса C выходы всегда регистровые, а в автомате класса F - комбинационные. На практике редко удаётся непосредственно реализовать автоматы классов C-F. Дело в том, что не всегда входные или выходные наборы определяют все коды внутренних состояний конечного автомата. Поэтому для построения автоматов классов C-F часто вводятся дополнительные элементы памяти путём задействования скрытых макроячеек ПЛИС.