Источник: Научная сессия МИФИ-99. Всероссийская научно-техническая конференция "Нейроинформатика-99". Сборник научных трудов. В 3 частях. Ч.1.- М.: МИФИ, 1999.- С.17-24.

Представление нейросетей

Данная работа посвящена разработке алгоритмов в концепции построения нейронных сетей с самостоятельной адаптацией (самоадаптирующихся нейросетей), предложенных в работах [[1],[2]], позволяющей значительно расширить возможности нейросетевых методов управления и обработки информации.

Пусть функционирование нейрона нейросети описывается уравнением

                        ,         ( 1 )

где A_i - внешние входные сигналы; a_j - входные сигналы от других нейронов; x_ij - веса межнейронных связей.

В работе [[3]] показано, что можно получить сколь угодно точное приближение любой непрерывной функции многих переменных, используя операции сложения и умножения на число, суперпозицию функций, линейные функции, а также одну произвольную непрерывную нелинейную функцию одного переменного. Для нейросетей это означает, что для получения указанного результата от функции активации нейрона требуется только нелинейность. Адаптивные возможности предлагаемых алгоритмов с ускоренным стохастическим поиском позволяют в полной мере реализовать потенциальные возможности нейросетей.

Целевая функция с помощью которой оценивается успешность обучения (адаптации) может быть задана, например, следующим образом:

                               ,                ( 2 )

где a_i^* - требуемые значения a_i. Однако существуют и другие возможности [1,2].

В работе [1] приведен метод случайного поиска с целью адаптации нейросети, построенный на флюктуациях весов межнейронных связей. Обладая всеми необходимыми качествами для создания самоадаптирующихся нейросетей, этот метод требует изменения N² параметров на каждом пробном шаге, где N - число формальных нейронов полносвязной нейросети. Метод адаптации, предложенный в работе [2] дает возможность сократить число изменяемых параметров поиска с N² до N за счет варьирования величинами r_i вместо x_ij, что обеспечивает ускорение обучающих алгоритмов. Дальнейшее ускорение осуществляется прогнозированием последующего направления поиска с использованием предыдущего опыта адаптации. Комбинация этих методов позволяет существенно ускорить процедуру случайного поиска, приближая ее быстродействие к детерминированным алгоритмам и сохраняя ее преимущества перед другими методами при построении самоадаптирующихся нейросетей.

 

Алгоритм самоадаптации нейросетей

В процессе адаптации (обучения) нейросети происходит подстройка весовых коэффициентов x_i до тех пор, пока не будет получен набор x_ij, удовлетворяющих условию H£m, где m максимально допустимая величина ошибки.

В работе предложенного в публикации [2] алгоритма можно выделить три повторяющихся этапа:

1. Сохранение текущих значений r_i⁰ для каждого нейрона и H⁰ для сети в целом.

2. Подбор методом случайного поиска величин r_i таким образом, чтобы выполнялось условие H<H⁰. При этом ошибка в уровне активности каждого нейрона сети может быть получена как

.

3. Подстройка весовых коэффициентов осуществляется с помощью преобразования

,

аналогичного обобщенному правилу [[4],[5]] Уидроу-Хоффа [[6]] (дельта-правилу), а коэффициент y пропорционален скорости изменения x_ij.

Изменение x_ij ведет к уменьшению Dr_i, приближающему величины r_i и, следовательно, a_i = f(r_i) к желаемым. При этом H стремится к минимально возможным значениям. То, что наилучшее приближение для r_i существует следует, из теоремы, приведенной в работе [[7]]. Для упрощения доказательства теоремы заменим r_i -A_i на U.

Для U Î R добиться наилучшего приближения можно линейной комбинацией   линейно независимых элементов . То есть можно найти такой элемент , что

.

Теорема: Элемент наилучшего приближения существует.

Доказательство: Исследуем соотношение (неравенство треугольника)

.

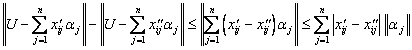Из него следует, что функция

является непрерывной функцией аргументов   при " UÎR. Пусть -евклидова норма вектора . Функция  непрерывна на единичной сфере  и, следовательно, в некоторой точке  достигает своей нижней грани  по сфере, причем , так как равенство   противоречит линейной независимости элементов . Для любого  справедлива оценка

.

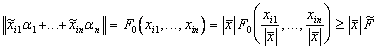Пусть . Функция  непрерывна в шаре ; следовательно в некоторой точке шара  она достигает своей нижней грани  по шару. Имеем . Вне этого шара выполняется соотношение

.

Таким образом

при всех возможных , что и требовалось доказать.

Отметим, что элементов наилучшего приближения может быть множество.

 

Адаптивная процедура

Для выполнения процедуры случайного поиска может быть использовано множество алгоритмов.

Одним из простейших является алгоритм с возвратом на неудачном шаге [[8]]. Он сводится к построению последовательности {r_i^k} по правилу:

,

где g ^k - некоторая положительная величина;  - какая-либо реализация n - мерной случайной величины  с известным законом распределения. Например, координаты x_h случайного вектора  могут представлять независимые случайные величины, равномерно распределенные на отрезке [-1,1].

Пусть k-е приближение уже известно. Функция H(a(r_i)) в уравнении (2) достигает минимума на некотором множестве QΠEⁿ,  r_i^kΠQ (k³ 0).

Алгоритм действует следующим образом. С помощью датчика случайных чисел получают некоторую реализацию случайного вектора  и в пространстве Eⁿ определяют точку r_i^k=r_i^k+gx, g =const>0. Если r_i^kΠQ и H(a(r_i^k))< H(a(r_i^k)), тогда r_i^k+1=r_i^k. Если r_i^kΠQ но H(a(r_i^k))³ H(a(r_i^k)), или r_i^kÏ Q, то сделанный шаг считается неудачным и полагается r_i^k+1=r_i^k.

В ситуации, когда требуемая точность достигнута - H£m, или r_i^k=r_i^k+1=r_i^k+2...=r_i^k+N, если N достаточно велико, точка r_i^k принимается в качестве искомой точки минимума.

 

Ускорение адаптивной процедуры

На этапе функционирования описываемые нейросети совпадают по быстродействию с нейросетями, обученными по детерминированным алгоритмам, но при обучении даже с учетом предложенных усовершенствований[1],  случайный поиск остается процессом достаточно медленным. Для его ускорения в работе [2] предложено использовать прогнозирование последующего направления поиска с использованием предыдущего опыта адаптации. Набор численных методов, пригодных для прогноза наилучшего изменения величин r_i (а для алгоритма, описанного в [1], величин x_ij), достаточно широк.

Приведем один из подходов, позволяющих осуществить подобную процедуру. Он представляет собой простую самонастраиваемую модель, основанную на вычислении так называемой экспоненциальной средней [[9]].

Поиск с вычислением экспоненциальной средней. В процессе случайного поиска возникает последовательность значений {r_i}, которые удовлетворяют условию улучшения функции оценки. Это временной ряд r_t, поведение которого прогнозируется (r_t - значение r_i в некоторый момент времени). Пусть временной ряд, генерируемый некоторой моделью, можно представить в виде можно представить в виде двух компонент

,

где величина e_t  генерируется случайным неавтокореллированным процессом с нулевым математическим ожиданием и конечной дисперсией, а величина d_t может быть сгенерирована либо детерминированной функцией, либо случайным процессом, либо какой-нибудь их комбинацией.

Вычисление и анализ тенденции динамического ряда можно осуществить с помощью его экспоненциального сглаживания. В его основе лежит расчет экспоненциальных средних. Экспоненциальное сглаживание описывается рекуррентной формулой

,

где S_t - значение экспоненциальной средней в момент t; n -параметр сглаживания, n =const, 0<n <1;  b=1-n.  Или через значения временного ряда r_t

,

где N - количество членов ряда; S₀ - некоторая величина, характеризующая начальные условия для первого применения формулы при t=1.

Так как b<1, то при N®¥  b^N®0, а

.

Тогда

 .

Таким образом, величина S_t является взвешенной суммой всех членов ряда.

Пусть ряд генерируется моделью

,

где a₁=const;  e_t - случайное неавтокоррелированное отклонение, или шум, со средним значением 0 и дисперсией s².

Применим к нему процедуру экспоненциального сглаживания. Тогда

.

Найдем математическое ожидание

 

и дисперсию

.

Так как 0<n  <1,  D(S_t)< D(r_t)=s². 

Таким образом, экспоненциальная средняя S_t имеет то же математическое ожидание, что и ряд r, но меньшую дисперсию. При высоком значении n  дисперсия экспоненциальной средней незначительно отличается от дисперсии ряда r.

Чтобы использовать экспоненциальную среднюю для краткосрочного прогнозирования используем ряд, который генерируется моделью

,

где a_1,t - варьируемый во времени средний уровень ряда;  e_t - случайное неавтокоррелированное отклонение с нулевым математическим ожиданием и дисперсией s ².

Прогнозная модель имеет вид

,

где  - прогноз, сделанный в момент t на t единиц времени (шагов) вперед;  - оценка a_1,t. Экспоненциальная средняя S_t служит оценкой для единственного параметра модели a_1,t

.

Все свойства экспоненциальной средней являются одновременно свойствами прогнозной модели.

Если S_t-1 - прогноз на 1 шаг вперед, то величина (r_t - S_t-1) является погрешностью этого прогноза, а новый прогноз S_t получается в репогрешностью этого прогноза, а новый прогноз S_t получается в результате корректировки предыдущего прогноза с учетом ошибки.

---