http://www.neuroproject.ru/gene.htm Эволюционная теория
Как известно, эволюционная теория утверждает, что жизнь на нашей планете возникла вначале лишь в простейших ее формах — в виде одноклеточных организмов. Эти формы постепенно усложнялись, приспосабливаясь к окружающей среде и порождая новые виды, и только через многие миллионы лет появились первые животные и люди. Можно сказать, что каждый биологический вид с течением времени улучшает свои качества так, чтобы наиболее эффективно справляться с важнейшими задачами выживания, самозащиты, размножения и т. д. Таким путем возникла защитная окраска у многих рыб и насекомых, панцирь у черепахи, яд у скорпиона и многие другие полезные приспособления.
С помощью эволюции природа постоянно оптимизирует все живое, находя подчас самые неординарные решения. С первого взгляда неясно, за счет чего происходит этот прогресс, однако ему есть научное объяснение. Дать это объяснение можно, основываясь всего на двух биологических механизмах — естественного отбора и генетического наследования.
Естественный отбор и генетическое наследование
Ключевую роль в эволюционной теории играет естественный отбор. Его суть состоит в том, что наиболее приспособленные особи лучше выживают и приносят больше потомства, чем менее приспособленные. Заметим, что сам по себе естественный отбор еще не обеспечивает развития биологического вида. Действительно, если предположить, что все потомки рождаются примерно одинаковыми, то различные поколения будут отличаться только по численности, но не по приспособленности. Поэтому очень важно изучить, каким образом происходит наследование, т. е. как свойства потомка зависят от свойств родителей.
Основной закон наследования интуитивно понятен каждому — он состоит в том, что потомки похожи на родителей. В частности, потомки более приспособленных родителей будут, скорее всего, одними из наиболее приспособленных в своем поколении. Чтобы понять, на чем основана эта похожесть, нам потребуется немного углубиться в строение животной клетки — в мир генов и хромосом.
Почти в каждой клетке любого животного имеется набор хромосом, несущих информацию об этом животном. Основная часть хромосомы — нить ДНК (молекула дезоксирибонуклеиновой кислоты), которая состоит из четырех видов специальных соединений — нуклеотидов, идущих в определенной последовательности. Нуклеотиды обозначаются буквами A, T, C и G, и именно порядок их следования кодирует все генетические свойства данного организма. Говоря более точно, ДНК определяет, какие химические реакции будут происходить в данной клетке, как она будет развиваться и какие функции выполнять.
Ген — это отрезок цепи ДНК, отвечающий за определенное свойство особи, например за цвет глаз, тип волос, цвет кожи и т. д. Вся совокупность генетических признаков человека кодируется посредством примерно 60 тыс. генов, суммарная длина которых составляет более 90 млн. нуклеотидов.
Различают два вида клеток: половые (такие, как сперматозоид и яйцеклетка) и соматические. В каждой соматической клетке человека содержится 46 хромосом. Эти 46 хромосом — на самом деле 23 пары, причем в каждой паре одна из хромосом получена от отца, а вторая — от матери. Парные хромосомы отвечают за одни и те же признаки — например, отцовская хромосома может содержать ген черного цвета глаз, а парная ей материнская — ген голубоглазости. Существуют определенные законы, управляющие участием тех или иных генов в развитии особи. В частности, в нашем примере потомок будет черноглазым, так как ген голубых глаз является “слабым” (рецессивным) и подавляется геном любого другого цвета.
В половых клетках хромосом только 23, и они непарные. При оплодотворении происходит слияние мужской и женской половых клеток и образуется клетка зародыша, содержащая как раз 46 хромосом. Какие свойства потомок получит от отца, а какие — от матери? Это зависит от того, какие именно половые клетки участвовали в оплодотворении. Дело в том, что процесс выработки половых клеток (так называемый мейоз) в организме подвержен случайностям, благодаря которым потомки все же во многом отличаются от своих родителей. При мейозе, в частности, происходит следующее: парные хромосомы соматической клетки сближаются вплотную, затем их нити ДНК разрываются в нескольких случайных местах и хромосомы обмениваются своими частями (рис. 1).
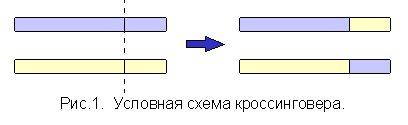 Этот процесс обеспечивает появление новых вариантов хромосом и носит название “кроссинговер”. Каждая из вновь появившихся хромосом окажется затем внутри одной из половых клеток, и ее генетическая информация может реализоваться в потомках данной особи.
Этот процесс обеспечивает появление новых вариантов хромосом и носит название “кроссинговер”. Каждая из вновь появившихся хромосом окажется затем внутри одной из половых клеток, и ее генетическая информация может реализоваться в потомках данной особи.
Второй важный фактор, влияющий на наследственность, — это мутации, которые выражаются в изменении некоторых участков ДНК. Мутации также случайны и могут быть вызваны различными внешними факторами, такими, как радиоактивное облучение. Если мутация произошла в половой клетке, то измененный ген может передаться потомку и проявиться в виде наследственной болезни либо в других новых свойствах потомка. Считается, что именно мутации являются причиной появления новых биологических видов, а кроссинговер определяет уже изменчивость внутри вида (например, генетические различия между людьми).
Задачи оптимизации
Как уже было отмечено выше, эволюция — это процесс постоянной оптимизации биологических видов. Теперь мы в состоянии понять, как происходит этот процесс. Естественный отбор гарантирует, что наиболее приспособленные особи дадут достаточно большое потомство, а благодаря генетическому наследованию мы можем быть уверены, что часть этого потомства не только сохранит высокую приспособленность родителей, но будет обладать и некоторыми новыми свойствами. Если эти новые свойства окажутся полезными, то с большой вероятностью они перейдут и в следующее поколение. Таким образом, происходит накопление полезных качеств и постепенное повышение приспособляемости биологического вида в целом. Зная, как решается задача оптимизации видов в природе, мы теперь применим похожий метод для решения различных реальных задач.
Задачи оптимизации — наиболее распространенный и важный для практики класс задач. Их приходится решать каждому из нас либо в быту, распределяя свое время между различными делами, либо на работе, добиваясь максимальной скорости работы программы или максимальной доходности компании — в зависимости от должности. Среди этих задач есть решаемые простым путем, но есть и такие, точное решение которых найти практически невозможно.
Введем обозначения и приведем несколько классических примеров. Как правило, в задаче оптимизации мы можем управлять несколькими параметрами (обозначим их значения через x1, x2, ..., xn, а нашей целью является максимизация (или минимизация) некоторой функции, f(x1, x2, ..., xn), зависящей от этих параметров. Функция f называется целевой функцией. Например, если требуется максимизировать целевую функцию “доход компании”, то управляемыми параметрами будут число сотрудников компании, объем производства, затраты на рекламу, цены на конечные продукты и т. д. Важно отметить, что эти параметры связаны между собой — в частности, при уменьшении числа сотрудников скорее всего упадет и объем производства.
Конечно, математики издавна занимались подобными задачами и разработали несколько методов их решения. В случае, если целевая функция достаточно гладкая и имеет только один локальный максимум (унимодальна), то оптимальное решение можно получить методом градиентного спуска. Идея этого метода состоит в том, что оптимальное решение получается итерациями. Берется случайная начальная точка, а затем в цикле происходит сдвиг этой точки на малый шаг, причем шаг делается в том направлении, в котором целевая функция растет быстрее всего. Недостатком градиентного алгоритма являются слишком высокие требования к функции — на практике унимодальность встречается крайне редко, а для неправильной функции градиентный метод часто приводит к неоптимальному ответу. Аналогичные проблемы возникают и с применением других математических методов. Во многих важных задачах параметры могут принимать лишь определенные значения, причем во всех остальных точках целевая функция не определена. Конечно, в этом случае не может быть и речи о ее гладкости и требуются принципиально другие подходы.
Классический пример такой задачи, известный как “задача коммивояжера” (Traveling Salesman Problem, TSP), формулируется так: коммивояжеру требуется объехать несколько городов, побывав в каждом один раз, и вернуться в исходную точку. Нужно найти кратчайший маршрут.
Самый простой способ найти оптимальное решение — перебрать все возможные значения параметров. При этом не нужно делать никаких предположений о свойствах целевой функции, а задать ее можно просто с помощью таблицы. Однако, чтобы решить таким способом задачу коммивояжера хотя бы для 20 городов, потребуется перебрать около 1019 маршрутов, что совершенно нереально ни для какого вычислительного центра. Таким образом, возникает необходимость в каком-либо новом методе оптимизации, пригодном для практики. В следующем разделе мы покажем, каким образом можно применить механизмы эволюционного процесса к нашим задачам. Фактически мы организуем искусственную эволюцию в специально построенном мире.
Работа генетического алгоритма
Представим себе искусственный мир, населенный множеством существ (особей), причем каждое существо — это некоторое решение нашей задачи. Будем считать особь тем более приспособленной, чем лучше соответствующее решение (чем большее значение целевой функции оно дает). Тогда задача максимизации целевой функции сводится к поиску наиболее приспособленного существа. Конечно, мы не можем поселить в наш виртуальный мир все существа сразу, так как их очень много. Вместо этого мы будем рассматривать много поколений, сменяющих друг друга. Теперь, если мы сумеем ввести в действие естественный отбор и генетическое наследование, то полученный мир будет подчиняться законам эволюции. Заметим, что, в соответствии с нашим определением приспособленности, целью этой искусственной эволюции будет как раз создание наилучших решений. Очевидно, эволюция — бесконечный процесс, в ходе которого приспособленность особей постепенно повышается. Принудительно остановив этот процесс через достаточно долгое время после его начала и выбрав наиболее приспособленную особь в текущем поколении, мы получим не абсолютно точный, но близкий к оптимальному ответ. Такова, вкратце, идея генетического алгоритма. Перейдем теперь к точным определениям и опишем работу генетического алгоритма более детально.
Для того чтобы говорить о генетическом наследовании, нужно снабдить наши существа хромосомами. В генетическом алгоритме хромосома — это некоторый числовой вектор, соответствующий подбираемому параметру, а набор хромосом данной особи определяет решение задачи. Какие именно векторы следует рассматривать в конкретной задаче, решает сам пользователь. Каждая из позиций вектора хромосомы называется ген.
Определим теперь понятия, соответствующие мутации и кроссинговеру в генетическом алгоритме.
Мутация — это преобразование хромосомы, случайно изменяющее одну или несколько ее позиций (генов). Наиболее распространенный вид мутаций — случайное изменение только одного из генов хромосомы.
Кроссинговер (в литературе по генетическим алгоритмам также употребляется название кроссовер или скрещивание) — это операция, при которой из двух хромосом порождается одна или несколько новых хромосом. В простейшем случае кроссинговер в генетическом алгоритме реализуется так же, как и в биологии (см. рис. 1). При этом хромосомы разрезаются в случайной точке и обмениваются частями между собой. Например, если хромосомы (1, 2, 3, 4, 5) и (0, 0, 0, 0, 0) разрезать между третьим и четвертым генами и обменять их части, то получатся потомки (1, 2, 3, 0, 0) и (0, 0, 0, 4, 5).
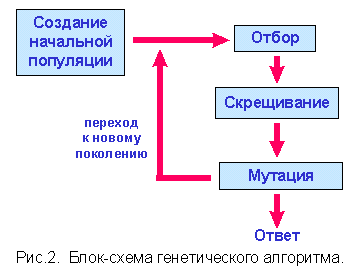
Блок-схема генетического алгоритма изображена на рис. 2. Вначале генерируется начальная популяция особей (индивидуумов), т.е. некоторый набор решений задачи. Как правило, это делается случайным образом. Затем мы должны смоделировать размножение внутри этой популяции. Для этого случайно отбираются несколько пар индивидуумов, производится скрещивание между хромосомами в каждой паре, а полученные новые хромосомы помещаются в популяцию нового поколения. В генетическом алгоритме сохраняется основной принцип естественного отбора — чем приспособленнее индивидуум (чем больше соответствующее ему значение целевой функции), тем с большей вероятностью он будет участвовать в скрещивании. Теперь моделируются мутации — в нескольких случайно выбранных особях нового поколения изменяются некоторые гены. Затем старая популяция частично или полностью уничтожается и мы переходим к рассмотрению следующего поколения. Популяция следующего поколения в большинстве реализаций генетических алгоритмов содержит столько же особей, сколько начальная, но в силу отбора приспособленность в ней в среднем выше. Теперь описанные процессы отбора, скрещивания и мутации повторяются уже для этой популяции и т. д.
В каждом следующем поколении мы будем наблюдать возникновение совершенно новых решений нашей задачи. Среди них будут как плохие, так и хорошие, но благодаря отбору число хороших решений будет возрастать. Заметим, что в природе не бывает абсолютных гарантий, и даже самый приспособленный тигр может погибнуть от ружейного выстрела, не оставив потомства. Имитируя эволюцию на компьютере, мы можем избегать подобных нежелательных событий и всегда сохранять жизнь лучшему из индивидуумов текущего поколения — такая методика называется “стратегией элитизма”.
Применение генетических алгоритмов
Чтобы использовать генетический алгоритм для решения практических задач, необходимо рассматривать более сложные варианты введенных выше понятий. Поясним это на примере задачи коммивояжера для 20 городов.
В качестве индивидуумов будем рассматривать маршруты обхода. Информацию о маршруте можно записать в виде одной хромосомы — вектора длины 20, где в первой позиции стоит номер первого города на пути следования, затем — номер второго города и т. д. Первое затруднение возникает, когда мы пытаемся определить мутации для таких хромосом — стандартная операция, изменяющая только одну позицию вектора, недопустима, так как приводит к некорректному маршруту. Но можно определить мутацию как перестановку значений двух случайно выбранных генов. При таком преобразовании путь следования меняется только в двух городах.
По условию задачи в рассматриваемых хромосомах каждый ген (номер города) должен встречаться только один раз. Такая разновидность хромосом называется “перечислимые хромосомы с уникальными генами” и часто используется в комбинаторных задачах. Стандартная операция скрещивания для этого типа хромосом опять же некорректна, поэтому здесь используется более сложная схема двухточечного скрещивания. За недостатком места мы не излагаем эту схему и рекомендуем заинтересованному читателю обратиться к специальной литературе.
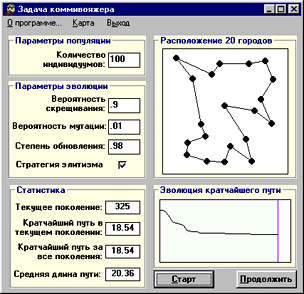
На рис. 3 изображен результат работы генетического алгоритма в задаче коммивояжера (мы использовали демонстрационную программу к пакету GeneHunter).
Указанные на рисунке значения параметров достаточно типичны — как и в природе, мутации происходят гораздо реже, чем скрещивания. В правом нижнем окне можно наблюдать, как изменялась длина кратчайшего в популяции маршрута в процессе эволюции. Эта длина монотонно убывает до некоторого момента, а затем стабилизируется. Найденный маршрут, вероятно, не является самым оптимальным, но близок к нему по длине — как правило, генетические алгоритмы “ошибаются” не более чем на 5—10%. Этот недостаток компенсируется для комбинаторных задач относительно высокой скоростью работы — в нашем примере ответ был получен за 25 секунд. На практике генетические алгоритмы нередко используют совместно с другими методами, которые позволяют повысить их точность.
Генетические алгоритмы используются не только в задачах комбинаторного типа (как TSP), но и в тех случаях, когда подбираемые параметры могут быть любыми действительными числами. Такова, например, задача оптимального распределения инвестиций; один из вариантов ее мы кратко опишем.
Пусть имеется некоторый капитал R, который нужно распределить между несколькими проектами с целью получения максимального дохода через определенный срок. Для каждого проекта задана функция дохода, приносимого проектом за этот срок, в зависимости от вложенной суммы. Используется также диверсификация, т. е. запрещено вкладывать в любой проект слишком большую сумму. В данной задаче целевой функцией является суммарная прибыль от инвестиций, а управляемыми параметрами — объемы вложений в каждый из проектов.
Подобные модели являются стандартными для экономистов, но в них рассматриваются только линейные функции доходности. В этом случае точное решение можно получить с помощью линейного программирования (симплекс-метод). Однако в реальных задачах нет оснований считать все функции линейными — более того, они могут быть даже разрывными. При этом целевая функция имеет сложный вид и не является унимодальной. В такой нелинейной ситуации стандартные методики работают плохо — в частности, симплекс-метод неприменим принципиально, а градиентный метод чаще всего приводит к неоптимальному решению.
Рассмотрим, каким образом решается эта задача для 10 проектов с помощью генетического алгоритма. Пусть каждый индивидуум имеет 10 хромосом, где k-я хромосома — это вектор из нулей и единиц, содержащий двоичную запись объема вложений в k-й проект. Если длина хромосомы равна 8 двоичным разрядам, то понадобится предварительная нормировка всех чисел в диапазон от 0 до 255. Такие хромосомы называются непрерывными и позволяют представлять значения произвольных числовых параметров. Мутации непрерывных хромосом случайным образом изменяют один бит (ген) в них, влияя таким образом на значение параметра. Кроссинговер также можно осуществлять стандартным образом, объединяя части соответствующих хромосом (с одинаковыми номерами) различных индивидуумов. Особенностью этой задачи является то, что суммарный инвестируемый капитал фиксирован и равен некоторому числу R. Очевидно, при мутациях и скрещивании могут получаться решения, для реализации которых требуется капитал больше или меньше R. В генетическом алгоритме используется специальный механизм работы с такими решениями, позволяющий учитывать ограничения типа “суммарный капитал = R” при подсчете приспособленности индивидуума. В процессе эволюции особи с сильным нарушением указанных ограничений вымирают. В результате работы алгоритма получается решение с суммарным капиталом, быть может, не равным в точности, но близким к заданному R. Как и в случае с задачей коммивояжера, эту погрешность следует считать платой за скорость поиска решения. Отметим, что полный перебор всех вариантов инвестирования в 10 проектов (для функций доходности, заданных на 256 точках) включает в себя более 1020 решений и нереализуем на практике.
Заключение — об эвристике в целом
В данной статье мы не приводим ни одного математического утверждения о сходимости или о качестве работы генетических алгоритмов — эта область слишком специальна и относится в основном к теоретическим модельным постановкам задач. Изложенный подход является эвристическим, т. е. показывает хорошие результаты на практике, но плохо поддается теоретическому исследованию и обоснованию. Естественно задать вопрос — следует ли пользоваться такими алгоритмами, не имеющими строгого математического обоснования? Как и в вопросе о нейронных сетях, здесь нельзя ответить однозначно. С одной стороны, в математике существует достаточно большой класс абсолютно надежных (в смысле гарантии получения точного решения) методов решения различных задач. С другой стороны, речь идет о действительно сложных практических задачах, в которых эти надежные методы часто неприменимы. Нередко эти задачи выглядят настолько необозримыми, что не предпринимается даже попыток их осмысленного решения. Например, фирма, занимающаяся транспортными перевозками, в современных условиях российского бизнеса скорее предпочтет нанять лишних водителей и повысить цены на свои услуги, чем оптимизировать маршруты и расписания поездок. На западном рынке, где уже давно действуют законы более или менее честной конкуренции, оптимальность деятельности компании значительно влияет на ее доходы и даже может стать решающим фактором для ее выживания. Поэтому любые идеи, позволяющие компании стать “умнее” своих конкурентов, находят там широкое применение. Генетические алгоритмы — реализация одной из наиболее популярных идей такого рода. Эта популярность вызвана, по-видимому, исключительной красотой подхода и его близостью к природному механизму. Подобным образом популярность нейросетевой технологии подогревается во многом ее сходством с работой мозга. По-настоящему активное развитие эвристических подходов, как мы видим, непосредственно связано с развитием свободного рынка и экономики в целом.