Лисицын Е. Radial based functions

Евгений Лисицын

Radial Based Functions

Источник: http://cgm.computergraphics.ru/content/view/43

Вступление

В данной статье приводится краткий обзор Функций Радиального Вида (RBF), математического аппарата, свойства которого делают его привлекательным для решения некоторых задач компьютерной графики и ряда других областей. В число задач, решаемых с помощью RBF, входят функциональная аппроксимация при моделировании временных серий и при распознавании образов; существуют RBF-реализации Байесовского критерия; RBF используются для моделирования непрерывных отображений.

Интерполяция функций

Использование RBF для интерполяции проиллюстрируем на задаче интерполирования в самом простом варианте: интерполяция функции f: R¹ > R¹. Исходные данные представляют из себя набор (сетку) значений аргумента функции и значения функции в узлах сетки:

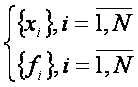
Необходимо получить интерполирующую функцию, которая в узлах сетки принимает указанные значения и обладает рядом свойств, зависящих от постановки задачи.

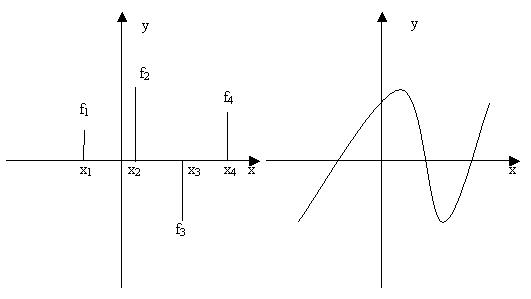
Задача интерполирования широко известна в математике, существует ряд глубоко изученных методов для ее решения, обладающих различными свойствами: интерполирование полиномом, интерполирование кубическими сплайнами, спектральная интерполяция и др. Известны проблемы, присущие указанным методам, которые в той или иной мере решает метод RBF.
Существенный недостаток интерполяции полиномом – рост степени полинома с ростом числа точек в сетке. Даже для сравнительно небольшого числа точек мы получаем полином степени, поведение которого очень нестабильно, т.е. имеются значительные скачки приближающей функции, которые могут сильно расходиться с поведением моделируемой функции:

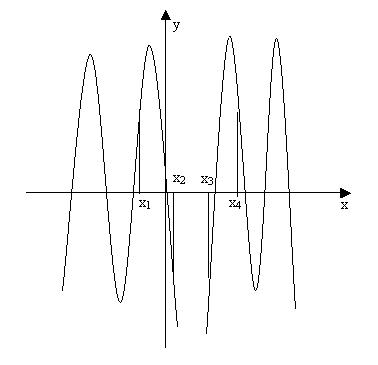
Интерполирование сплайнами – метод, дающий более стабильный результат, однако имеющий свои недостатки. Во-первых это достаточно громоздкий вид результирующей функции. Во-вторых, метод испытывает известные трудности (в случае интерполяции функции R?R этот недостаток не проявляется) в случае иррегулярных входных данных. Уже при интерполяции R²?R необходимо разбиение исходных данных на куски регулярной формы (tri- или quad-patches). В случае, когда исходная сетка обладает известной степенью нерегулярности, усложняется, подчас значительно, задача выбора отдельных кусков. В-третьих, объем сплайн-коэффициентов подчас превышает объем исходных данных, и это приводит к значительных вычислительным нагрузкам.

Рассмотрим решение задачи интерполирования (в обобщенном случае) при помощи RBF.
Постановка задачи в этом случае такова: восстановить векторное поле, заданное на конечном множестве. Формально:

Предлагается следующий вид интерполирующей функции (в общем виде):

или
,

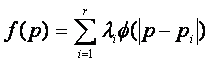где
- константы, которые полностью задают функцию для заданной ,
- функция радиального базиса, ее выбор определяет свойства результирующей функции (см. ниже)

Ограничения:

- условие интерполяции

- граничные условия

Имеет r+2 свободных переменных и r+2 ограничения, что дает полностью определенную СЛАУ. Принимаем обозначения:

- матрица системы

-правая часть

- вектор-решение

В принятых обозначениях решение задачи интерполирования сводится к решению системы:

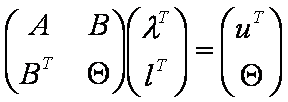(1)

Отметим, что многие применяемые в практике формы RBF обеспечивают различные свойства матрицы А (положительную определенность, диагональное преобладание и др.), которые позволяют применять специализированные численные методы, сокращающие объем вычислений для решения системы.

В отношении рассмотренных выше проблем полиномиального и сплайнового методов заметим, что:
- метод RBF инвариантен относительно структуры входных данных;
- стабильность результирующей RBF, т.е. отсутствие резких скачков, сводится в данном случае к устойчивости СЛАУ (1), которая, в свою очередь, определяется выбором RBF.

Виды RBF

Назовем несколько видов RBF, применяющихся на практике в различных задачах:

1) - степенная RBF. Аналог интерполяции полиномом.
2) - thin-plate spline. Используется для интерполяции гладких функций двух переменных, так как обеспечивает наиболее гладкое приближение.
3)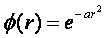 - гауссиан. Локализована вокруг центра. Примеры использования – [10].
4) - мультиквадратичная функция. Локализована вокруг центра.

Функции, локализованные вокруг центра, дают матрицу А специального вида, который позволяет уменьшить объем вычислений, однако отрицательно сказывается на экстраполирующих свойствах приближения. Для еще большего сокращения объема вычислений применяются функции с явно ограниченной областью, где функция отличная от нуля:

В этом случае число ненулевых значений в матрице A резко сокращается, вместе с ним уменьшается объем необходимых для решения задачи вычислений. Недостатком использования таких функций

Radial Based Networks

Описанный выше метод является частным случаем механизма, получившего название сети функций радиального базиса (Radial Based Network – RBN или Radial Based Function Neural Network - RBFNN). Термин RBFNN появился в конце 80-х годов, однако его корни уходят в значительно более старые техники распознавания образов (функции потенциала, кластеризация, функциональная аппроксимация [1]). Термин обозначает нейронные сети специального вида:

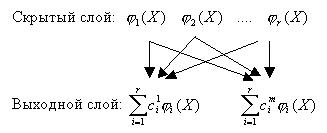
Здесь- активационная функция радиального базиса. В RBFNN используются локализованные функции, активизирующиеся только в некоторой окрестности центра X_i. Это дает возможность строить топологию сети таким образом, что отдельные части входного сигнала активизируют только определенную часть нейронов скрытого слоя.
Построение RBFNN включает в себя: указание вида активационной функции, числа нейронов скрытого слоя, критерий для моделирования конкретной задачи и алгоритм обучения сети. Под обучением RBFNN понимается нахождение весов

Заключение. Применение RBF.
В данной статье был представлен краткий обзор методов, основанный на применении функций радиального базиса (RBF). Сети RBF предоставляют мощный и эффективный метод функциональной аппроксимации и интерполяции [2,3,7,8]. В силу своей нелинейной природы RBFNN могут моделировать сложные отображения, реализация которых с помощью персептронных сетей требует нескольких промежуточных слоев. Они успешно применяются при решении целого ряда задач:
- моделирование случайных процессов [5,9]
- моделирование параметров электронных приборов, выравнивание сигнала [4,11,12]
- распознавание речи [11,13]
- восстановление изображения [14]
- shape-from-shading [15]
- моделирование трехмерных объектов [8,16,17] и др.