Математические основы деформируемых моделей
Авторы: Tim McInerney, Demetri Terzopoulos
Перевел: Алексей Винокуров
Источник: Medical Image Analysis, 1(2):91–108, 1996
Математические основы деформируемых моделей представляют собой совокупность геометрии, физики и теории приближения. Геометрия служит для отображения формы объекта, физика ограничивает рамки, в которых форма может изменяться во времени и пространстве, а теория оптимальной аппроксимации формально обосновывает требования к устройствам, которые служат для приведения моделей в соответствие с данными измерений.
Геометрия деформируемых моделей, как правило, позволяет охватить широкий спектр разнообразных форм путем использования геометрических представлений, имеющих много степеней свободы, такие как сплайны. Тем не менее, эта модель остается легко управляемой, потому что степени свободы обычно не разрешено устанавливать независимо, они обусловлены законами физики, которые возводят интуитивно обозначаемое поведение на геометрическом основании. Термин «деформируемые модели (точнее – модели, способные к деформации)», изначально происходит от применения теории упругости на физическом уровне, как правило, в границах установок Лагранжевой динамики. Физическая интерпретация рассматривает деформируемые модели в качестве упругих тел, реагирующих естественным образом на приложенные силы и давление. Как правило, функции энергии деформации, определенные рамками геометрических степеней свободы, связаны с деформируемой моделью. Энергия монотонно возрастает по мере деформации модели относительно конкретного «естественного состояния» или «состояния покоя» и часто включает в себя величины, ограничивающие гладкость симметрии модели. (В привязке к Лагранжевым переменным), энергия деформации вызывает внутренние упругие силы в модели. С точки зрения физического подхода к классической оптимальной аппроксимации, функции внешней потенциальной энергии определены в пределах, интересующих нас данных, к которым должна быть (приспособлена, подогнана) модель.
Деформируемые кривые, поверхности и объемные тела (1, 2, 3мерные модели) завоевали популярность после того, как они были предложены к использованию в «машинном зрении» (техническое зрение направление искусственного интеллекта и обработки изображений, занимающееся обработкой изображений реальной действительности), (Terzopoulos и другие 1988), и компьютерной графике (Terzopoulos и Fleischer 1988) в середине 1980х. Terzopoulos представил теорию непрерывных (многомерных) деформируемых моделей в установках Лагранжевой динамики (Terzopoulos 1986a), основанных на энергиях деформации в форме обобщенных сплайнов (Terzopoulos 1986b). Среди предшественников деформируемых моделей, которые сейчас широко используются — «подпружиненные» образцы Fischler’а и Elshlager’а (1973) и технология «резиновых масок» Widrow’а (1973).
Деформируемая модель, привлекшая наибольшее внимание на данный момент широко известна как «snakes» (змеи) (Kass и другие 1988). Snakes , или «деформируемые контурные модели», представляют собой частный случай общей теории многомерной деформируемой модели (Terzopoulos 1986a).

Мы рассмотрим их простую формулировку в конце этого раздела, чтобы проиллюстрировать на конкретном примере основы математического аппарата, присутствующего во многих деформируемых моделях.
Snakes — плоские деформируемые контуры, полезные для некоторых задач анализа изображений. Они часто используются для аппроксимации локаций и форм границ объектов в изображениях, основанных на разумном предположении, что границы кусочно–непрерывные или гладкие (рис. 1). В изначальной форме, математическая формулировка Snakes исходит из теории оптимальной аппроксимации с вовлечением функционалов.
2.1 Минимизирующие энергию деформируемые модели
С точки зрения геометрии, snake это параметрический контур, вложенный в плоскость изображения (x,y) R. Контур представлен как v(s) = (x(s),y(s)), где х и у — функции координат, а s [0,1] — параметрическая область определения. Форма контура, подчинена изображению I (x,y) и обусловлена функционалом E(v) = S(v) + P(v) (1)
Функционал может быть рассмотрен как отображение энергии контура, а окончательная форма контура соответствует минимуму этой энергии. Первый член функционала,
это внутренняя энергия деформации. Он характеризует деформацию растяжимого, гибкого контура. Две физических параметрических функции определяют симулируемые физические характеристики контура: w1(s) контролирует натяжение контура, в то время как w2(s) контролирует его неэластичность. Второй член в (1) связывает snake к изображению. Традиционно,
где P(x,y) обозначает функцию скалярного потенциала, определенную на плоскости изображения. Чтобы применить snakes к изображениям, разработаны внешние потенциалы, локальные минимумы которых совпадают с экстремумами интенсивности, границами области и другими примечательными точками изображения. К примеру, контур будет привлекаться к краям интенсивности в изображении I(x,y), путем выбора потенциала
Значения неотрицательных функций w1(s) и w2(s) определяют степень, до которой snake может растягиваться или сгибаться в любой точке s на snake. К примеру, увеличение магнитуды w1(s) увеличивает “натяжение” и стремится устранить внешние петли и волны путем уменьшения длины snake. С увеличением w2(s), возрастает “жесткость” snake и появляется тенденция к «сглаживанию» и уменьшению гибкости snake.Установка значения одной или обеих этих функций на 0 в точке s разрешает сосредоточенные неоднородности в точке s на контуре.
где с контролирует магнитуду потенциала а G * I обозначает изображение, свернутое (Гауссовским) сглаживающим фильтром, чья характеристическая ширина sigma контролирует пространственную меру локального минимума Р
В соответствии с вариационным исчислением, контур v(s), минимизирующий энергию E(v), дожжен удовлетворять уравнению Эйлера-Лагранжа:

Это векторное дифференциальное уравнение в частных производных выражает баланс внешних и внутренних сил, когда контур находится в равновесии. Первые два члена отражают внутренние силы растяжения и изгиба соответственно, в то время как третий член соответствует внешним силам, привязывающим snake к данным изображения. Обычный подход к решению (4) — путем применения численных алгоритмов. (см. 2.3).
2.2 Динамические деформируемые модели
Поскольку естественно рассматривать минимизацию энергии как статическую проблему, действенным подходом к вычислению локальных минимумов таких функционалов, как (1), является создание динамической системы, управляемой функционалом и позволение системе достигать равновесия. Система может быть создана применением принципов Лагранжевой механики, что ведет к динамически деформируемым моделям, объединяющим описание формы и движения, что позволяет измерить не только статическую форму, но и изменение формы во времени.
Динамические модели ценны для анализа изображений в медицине, так как большинство анатомических структур поддаются деформации и постоянно подвержены нежестким движениям в живом организме. Более того, динамические модели выявляют интуитивно значимое физическое поведение, что делает их изменения подверженным воздействию пользователей (рис. 2).
Простой пример — динамический snake, который может быть представлен с помощью изменяемого во времени контура v(s,t) = (x(s,t),y(s,t))^T с плотностью масс m(x) и плотностью демпфирования (затухания) y(s). Уравнения движения Лагранжа для snake с внутренней энергией, заданной (2) и внешней энергией, заданной (3), это
Первые два члена в левой части этого дифференциального уравнения в частных производных представляют силы инерции и демпфирования. По отношению к (4), остающиеся члены представляют внешние силы растягивания и сгибания, в то время как правая часть отражает внешние силы. Равновесие достигается, когда внутренние и внешние силы уравновешиваются и контур приходит в состояние покоя (то есть,
![]() ), что удовлетворяет условию равновесия
), что удовлетворяет условию равновесия
2.3 Дискретизация и численное симулирование.
Чтобы численно вычислить решение минимума энергии, необходимо дискретизировать энергию E(v). Обычный подход — представит непрерывную геометрическую модель v в понятиях линейной комбинации основных функций локальной поддержки или глобальной поддержки. Конечные элементы (Zienkiewicz и Taylor 1989), конечные разности (Press и другие 1992), и геометрические сплайны (Farin 1993) являются методами локального представления, тогда как основанием метода Fourier (Ballard и Brown 1982) являются методы глобального представления. Непрерывная модель v(s) представляется в дискретной форме вектором параметров формы, объединенным с базисной функцией. Дискретная форма энергий, такая как E(v) для snake может быть записана как

Где K называется матрицей жесткости, а P(u) — дискретная версия внешних потенциалов. Решение минимума энергии получается из приравнивания градиента (6) к 0, что эквивалентно решению системы алгебраических уравнений
Где f — обобщенный вектор внешних сил.
Дискретизированная версия уравнений динамики Лагранжа (5) может быть записана как система обыкновенных дифференциальных уравнений второго порядка для u(t):
Mu’’ + Cu’ + Ku = f
Где M — матрица масс, а C — матрица демпфирования. Производные времени в (5) аппроксимированы конечными разностями и выражают или явные или неявные методы численного интегрирования по времени применяются для симулирования результирующей системы обыкновенных дифференциальных уравнений для параметров формы u
2.4 Вероятностные деформируемые модели
Альтернативный взгляд на деформируемые модели проистекает из вычисления процесса подгонки модели в вероятностных рамках. Это позволяет объединять характеристики предыдущей и сенсорной моделей при условиях распределения вероятностей. Вероятностные рамки также предоставляют некоторую меру неопределенности предполагаемых параметров формы после того, как модель подогнана к данным изображения. (Szeliski 1990).
Пусть u представляет параметры формы деформируемой модели с априорной вероятностью p(u).
Пусть p(I|u) - модель представления изображений(сенсорная модель) – возможность созданья изображения I при заданной модели u.
Теорема Байеса
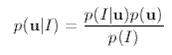
Выражает апостериорная вероятность p(I|u) модели заданного изображения, на основе модели представления изображений и априорной вероятности модели и изображения. Измерение внутренней энергии деформируемой модели легко преобразовать в априорное распределение в ожидаемые формы, где формы с низкими показателями энергии являться более вероятными. Это достигается, используя распределение контура Больцмана (или Гиббса),
где S(u) - это дискретизированная версия S(v) в (2) и Zs - это нормирующая постоянная называемая функция разбиения. Эта априорная модель комбинируется с простой сенсорной моделью, основанной на линейных измерениях с гауссовым шумом,
Где P(u) - дискретная версия потенциала P(v), который является функцией изображения I(x,y). Модели могут быть подобраны путем поиска u, которая локально максимизирует p(u|I) в (9).
Это известно как максимальное апостериорное значение. Вместе с вышеупомянутой конструкцией оно способствует достижению такого же результата, как и минимизация (1), конфигурации энергии деформируемой модели заданного изображения. Вероятностные рамки могут быть расширены путем использования априорной модели с переменными параметрами или системной модели, в сочетании с сенсорной моделью, в результате чего получается фильтр Кальмана. Системная модель описывает ожидаемое изменение параметров формы u во времени. Если уравнения механики, применяемые при описании физической модели snake (8) используются как системная модель, то результатом является алгоритм последовательного оценивания, известный как “Kalman snakes” (Terzopoulos and Szeliski 1992).