Surface reconstruction and segmentation based on deformable models
Автор: Johan Montagnat
Источник: http://www-sop.inria.fr/epidaure/personnel/Johan.Montagnat/ORASIS97/hybrid.html
About work
I am studying deformable models for reconstruction, geometric representation and segmentation of 2D or 3D data. Here is an attempt to build a robust framework for deformable models: the hybrid deformation scheme.
Introduction
Two main approaches have been proposed to deform models. The deformable models framework or snakes apply localy forces computed from the data. This leads to models with a very large shape expressiveness. Models are made resistant to noisy data or outliers by the introduction of regularizing forces in the deformation framework. However, those constraints are only local and this framework does not allow a global shape control.
The registration framework is based on an Iterative Closest Point (ICP) algorithm to iteratively apply global transformations (rigid, affine...) on a model. At each step of the ICP, a transformation g in a space G is computed by minimizing a least square error criterion. The registration allows to control deformations by limiting the search space G thus reducing the number of degrees of freedom of the model. Though, it may happen that the number of degrees of freedom let to the model does not allow it to deform enough to match the shape it is supposed to represent.
We propose a hybrid deformation framework which tries to take advantage of both previous approaches. By considering the global transformations computed in the registration framework as a deformation field similar to the local deformation field of the deformable models scheme, we apply to each vertex of the model a combined force:
f(i) = (1-l) * GlobalForce(i) + l * LocalForce(i)
where l is a locality parameter. It is possible to apply to the model in this single framework completely local (l = 1), completely global (l = 0) as well as any intermediate (0 < l < 1) force between those two ends.
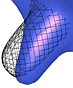
The hybrid framework introduce a global constraint in the deformation process which may be scale through the l parameter. It make models more robust: they are less noise and outliers sensitive, Moreover, the geometric quality of meshes produced by the deformation scheme are better.
Another advantage is that the hybrid framework allows to introduce problem specific constraints. By replacing the global transformation by a given transformation, it is possible to control the model's behavior. We introduced an axial constraint that make an axial model bend with its axis.
Implementation
We implemented 2D and 3D deformable model software. For 3D we are using simplex meshes developped by Herve Delingette. They are an intuitive extension of snakes in the 3D case that allow to define the curvature (the simplex angle) on each model vertex and the local shape in an elegant way.
Two evaluate global transformations required by the hybrid framework, we used the work of Xavier Pennec and Jerome Declerck on rigid transformations, similarities, affine and cubic B-spline transformation evaluation.
Results
Here are various result obtained by deforming models using the hybrid framework.
- Face reconstruction with an adapted geometry model.
- Lips tracking in a video sequence
- Segmentation of human anatomical structures
- Segmentation of vessels using an axial constraint
Applications
This work was motivated by the developpement of a laparoscopic surgery simulator whose first step is the segmentation of the liver tissue from abdominal CT-scan images. The surgery simulator project involves Luc Soler for the segmentation of vascular trees and the antomical segmentation, Stephane Cotin for the real time and realitic liver model deformations and Herve Delingette , supervisor.
As can be seen in the results, the hybrid framework finds many other applications than segmentation. It produces model with high geometric qualities. This is a fundamental hypothesis to perform a shape statistical analysis of the model obtained. In the future we plane to increase the segmentation accuracy by introducing in the deformation framework an a priori knowledge of the possible model shapes.