Производственное планирование и производственный контроль направлены на решения задач приобретения, использования и распределение ресурсов производства, с целью удовлетворения требований покупателя эффективным образом. Типичные решения используют такие показатели как уровень рабочей силы, размеры партии производства, назначение сверхурочных и налаживание хода производства. для принятия решений данного контекста широко применяются модели оптимизации.
В этой статье мы сосредоточимся на моделях оптимизации для планирования производства дискретных частей, условий производства партии.
Цель статьи - обеспечить краткий обзор применимых моделей оптимизации; представить их формулировки и кратко описать решение таких моделей.
Существует огромный диапазон и типичных формулировок таких моделей, так же как и описаний методов их решений. Автор статьи не ставит целью охватить все аспекты, скорее пытается выборать, основываясь на своих субъективных суждениях, какая информация является наиболее важной.
Планирование Производства: Модели линейного программирования
В этой части представлена основная модель оптимизации производства в разрезе следующих условий:
- имеется множество товаров с независимым спросом,
- множество разделенных ресурсов,
- временные периоды - большие
- издержки линейны
Определяем неизвестные и параметры модели:
Неизвестные:
- pit производство товара i во временном периоде t
- qit количество имеющегося запаса товара i на конец периода t
Параметры:
- T, I, K количество периодов времени, товаров, ресурсов соответственно
- aik количество ресурса k требуемого для производства единицы товара i
- bik количество ресурса k доступного в период времани t
- dit спрос на товар i в период t
- cpit стоимость переменных издержек для производства товара i в период времени t
- cqit стоимость хранения на складе единицы товара i в период времени t
Мы теперь формулируем линейную модель P1:

Целевая функция (1) минимизирует переменные издержки производства и издержки на хранение для всех товаров по всем T периодам.
Уравнение (2) является ограничением на запас продукции на складе, которое уравнивает поставку товара в период T со спросом на него. В любой период времени наличие товара есть запас предшествующего периода qi, t-1 плюс производство в настоящем периоде времени pit.
Этот запас может использоваться для удовлетворения спроса в данном промежутке времени dit, или хранения на складе qit. Поскольку требутся чтоб запас быть неотрицательным, то ограничения устанавливают, что требование удовлетворено для каждого товара в каждом периоде. Так же заданы начальные запасы для каждого товара, а именно, qi0.
Уравнение (3) является ограничением по ресурсу.
Производство в каждый период ограничено доступностью ресурсов, т.е. производство одной единицы товара i требует единицы ресурса aik для k = 1, 2... K, где К - количество ресурса. Как правило, ресурсами могут выступать различные типы рабочей силы,
материальное оборудование, транспорт и т.д.
Число неизвестных - 2IT, и число ограничений - IT + KT. В реальности, мы можем решить P1 любым алгоритмом решения задач линейного программирования, например, симплекс методом.
Далее кратко описаны модификации к основной модели, которая была представлена выше. Они описаны как независимые модели, однако, большинство задач, встречающихся в реальных условиях требуют комбинаций таких модификаций.
Планирование Спроса: Потерянные Продажи
Иногда мы можем не удовлетворять спрос в полном объёме в каком - либо периоде времени.
В действительности, может и не быть достаточного количества ресурсов для удовлетворения всего спроса. Проблема оптимизации состоит в том, чтобы решить какой спрос удовлетворить и как. предположим, что спрос, который не может быть неудовлетворён в данном периоде, является недопулученным доходом.
Кроме того, фирма может быть подвержена потере своей репутации, что может проявиться в уменьшении будущих продаж. Эту потерянную стоимость продаж очень трудно посчитать, поскольку она представляет собой будущее неизвестное воздействие от плохого обслуживания в настоящем.
Появляется новая проблема планирования - нужно максимизировать поступление доходов производства, запасов и минимизировать потерянные коммерческие затраты. Мы вводим дополнительное обозначения и затем заявляем модель:
Неизвестные:
- uit неудовлетворённый спрос на продукт i в периоде времени t
Параметры:
- rit доход единицы товара i в период t
- cuit стоимость единицы неудовлетворенного спроса на товар i в период времени t

Функция цели, в сравнении с классической моделью, была изменена, с целью включения дохода производства и стоимости потерянных продаж. Потенциальный доход, 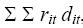 является константой и может входить в функцию цели. В этом случае, задаче вновь сводится к задаче минимизации стоимости, а стоимость, так называемых, потерянных продаж включает в себя недополученный доход. является константой и может входить в функцию цели. В этом случае, задаче вновь сводится к задаче минимизации стоимости, а стоимость, так называемых, потерянных продаж включает в себя недополученный доход.
Кроме того, в P2 ограничение на запас продукта было изменилось, с целью разрешения выбора удовлетворения требованию; таким образом равенство спроса в данный период может соблюдаться по отношению к производству или запасу,
или не удовлетворяться вообще. Ограничение ресурса (3) остается неизменным.
…
Планирование Ресурсов
До сих пор мы считали, что уровни ресурса установлены и заданы. Однако,иногда важным элементом задачи планирования есть решение о том как распределить ресурсы по всему плановому горизонту. Например, можно изменять количество рабочей силы посредством найма и увольнения. Hansmann и Hess (1960) разработали самый ранний пример модели такого типа.
Пусть имеется только один тип ресурса, например, рабочая сила.
Мы вводим дополнительное условия и описываем модель:
Неизвестные:
- wt уровень рабочей силы в период времени t
- ht изменения уровня рабочей силы, за счёт найма в период времени t
- ft изменение уровня рабочей силы, за счёт увольнений в период времени t
Параметры:
- ai количество рабочей силы, которая требуется на единицу производства товара i
- cwt переменная стоимость единицы рабочей силы в период времени t
- cht переменная стоимость найма в период времени t
- cft переменная стоимость увольнения в период времени t

Мы добавляем переменную стоимость для рабочей силы к функции цели, наряду с затратами найма и увольнения рабочих. Стоимость найма включает затраты на поиск и вербовку претендентов, а также на обучение персонала. Стоимость увольнения включает затраты на трудоустройство уволенных и
переквалификацию перемещенных рабочих, неустойки; также может быть стоимость, потерянная за счёт низкой производительности из-за снижения желания и мотивов работников в связи с постоянными и временными увольнениями.
Ограничение баланса запаса (2) остается тем же самым что и в P1, отражаем рабочую силу как основную переменную. Мы тогда добавляем новый набор ограничений баланса для того, чтобы планировать рабочую силу:
рабочая сила в период t есть то, что осталось с предшествующего периода плюс издержки на новую высокау разрешающую способность минус запущенное число.
Мы заявили P5 для единственного ресурса - рабочей силы.
Модель расширяется немедленно, чтобы включить другие ресурсы, с помощью которых можно управлять горизонтом планирования.
Кроме того, можно предложить и другие предположения для того, чтобы смоделировать временные задержки регулируя уровень ресурса. Можно предположить, что существуют пределы на скорость формирования новых рабочих мест в связи с обучением. Если есть ограничение на обучение
ресурсов, то это налагает ограничение на h t. Альтернативно, новая высокая разрешающая способность может быть менее производительной, пока они не приобрели опыт. В этом случае, мы изменяем
формулировку к различным категориям рабочих, в зависимости от их срока пребывания и уровень опыта.
Другое общее изменение этой модели состоит в наличии два трудовых классов, скажем, постоянные служащие и временные служащие. В этих классах отличаются коэффициенты стоимости, и возможно факторы эффективности.
Постоянные служащие имеют более высоки стоимости наема и увольнения, поскольку они получают более подробное обучение и имеют больше прав, лучше защищены от временных увольнений. Но их переменные издержки производства, нормализованные их производительностью, должны быть ниже чем для временных рабочих. Проблема планирования в таком случае влечет за собой
управление и планирование обоих классов работы по горизонту планирования.
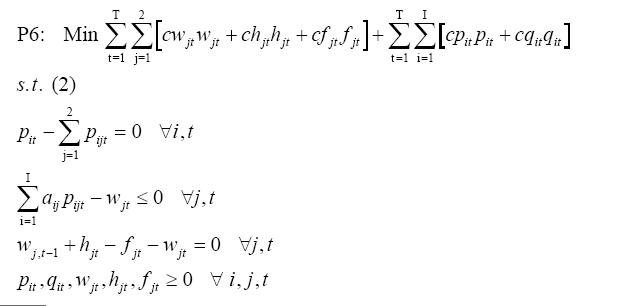
Для законченности, мы пересматриваем P5 для двух классов рабочей силы:
По сравнению с P5 у нас есть переменные решения для обоих трудовых классов, так же как для решений по их найму и увольнению, которые необходимы для моделирования различий стоимости и т.д.
|





