MODELS FOR PHOTOGRAMMETRIC BUILDING RECONSTRUCTION

Braun C., Lang F., Schickler W., Forstner W.
Institut fur Photogrammetrie,
Kolbe T. H., Steinhage V., Cremers A. B., Plumer L.
Institut fur Informatik
Universitat Bonn

ABSTRACT

The paper discusses the modeling necessary for recovering man made objects - in this case buildings - in complex scenes from digital imagery. The approach addresses all levels of image analysis for deriving semantically meaningful descriptions of the scene from the image, via the geometrical/physical model of the objects and their counterparts in the image. The central link between raster image and scene are network-like organized aspects of parts of the objects. This is achieved by generically modelling the objects using parametrized volume primitives together with the application specific constraints, which seems to be adequate for many types of buildings. The paper sketches the various interrelationships between the different models and their use for feature extraction, hypothesis generation and verification.

1 Introduction

Three-dimensional building extraction from digital images is needed for an increasing number of tasks related to measurement, planning, construction, environment, transportation, energy and property management. Photogrammetric methods are well established but show inefficiencies due to the extensive amount of data compared with 2.5-D applications. The integration of automatic or at least semiautomatic image understanding tools into photogrammetry seems to be an appropi-ate way to achieve efficiency in three-dimensional data acquisition.

The digital images generally contain a great deal of information which is irrelevant with respect to the given task of building extraction, e.g. vegetation, cars, building details like windows, stairs etc. On the other hand there is a loss of relevant information due to the projection of three-dimensional shapes into two-dimensional images. Furthermore occlusions, low contrast or unfavorable perspectives will cause a loss of information. Therefore a promising concept for automatical or semi-automatical building reconstruction should incorporate a sufficiantly complete model of the objects of interest and of their relationships.

In various projects we investigate on the extraction of buildings from digital images. The paper gives an overview of different approaches to model three-dimensional shapes and two-dimensional images, and discusses a new concept for three-dimensional building reconstruction based on geometric modeling.

2 APPROACHES TO OBJECT AND IMAGE MODELING

On the one hand we find - mostly theoretically oriented - approaches which employ generic polyhedral modeling schemes for object descriptions with variable topology. On the other hand we find - especially pragmatic motivated - systems which utilize parametrized object models (i.e. fixed topology and variable geometry) or CAD models (i.e. fixed topology and fixed geometry). The applicability of these approaches depends on the a priori knowledge of the concrete application.

2.1 Polyhedral Models

Polyhedra in many applications have shown to be adequate approximative models for real - especially man made - object shapes. Basic research about qualitative interpretation of line drawings polyhedra was done by Clowes 1971, Huffman 1971 and Waltz 1975. Sugihara 1986 established an algebraic method for the verification of such line drawings. The approach has been extended by Kanatani 1990 and Heyden 1994 for solving inconsistencies of the line drawings in a least-squares manner. Herman and Kanade 1987 used a polyhedral model expanded by heuristics in their MOSAIC-System for the reconstruction of buildings. Braun 1994 also employs a generic polyhedral model within the task of building reconstruction via monocular image analysis where heuristics encode knowledge about line geometry, vanishing points, and orthogonal trihedral corners and uses this in a joint maximum-likelihood estimation procedure. Steinhage 1993 utilized generic polyhedral modeling within a multi-view stereo-vision and dealed with the problems due to occlusions and non generic views.

The degree of automation of all these approaches depends on the results of the feature extraction which deals in most cases with the extraction of the contour lines of the projected objects. Of course polyhedral object modeling doesn't restrict the reconstruction to those shapes which correspond to buildings. On the other hand polyhedral models only describe the geometric shape of their surfaces and are restricted to planar surfaces.

2.2 Parametrized Models for Object Reconstruction

Most buildings can be described in terms of simple primitive shapes. Therefore parametrized models describing the most common building types suggest to be a promising tool for a pragmatic solution. Motivated by the research results of QUAng a Strat 1991 this approach is used within the semi-automatic system of LAN nd Schickler 1993: the three-dimensional building extraction consists in the selection of a basic building type model, its projection into the digital image, followed by a coarse interactive adjustment of the form and position parameters of the model and an automatic fitting based on extracted intensity edges from all images of the observed building.

The advantage of this approach is that it provides the complete modeling of a building by a parametrized volumetric primitive. Indeed the practical use of such a system depends on the capacity of the assembled building types: beside simple building types, urban scenes show irregular houses and very complex combinations of buildings and building parts. These buildings and building formations cannot be modeled with this approach. Several researchers therefore assumed buildings to consist of a set of parametrized building blocks, mostly boxes (cf. Lin et al. 1994b, Lin et al. 1994a, McKeown 1990). However, relations between the primitives usually have not been used for constraining the interpretation. But a modeling scheme for building reconstruction has to provide geometrical variations and also capabilities to describe topological variants of shapes and their potential relationships.

2.3 CAD Models for Object Identificaton

CAD systems offer elaborated techniques for the representation of complex spatial objects which are mainly adressed to and suited for construction tasks. These representation schemes include boundary representation (B-Rep) and constructive solid modeling (CSG). CAD models are employed in computer vision tasks within monocular image analysis as well as in multi-view approaches (e.g. Hansen and Henderson 1989; Liu and Tsai 1990; Chiou et al. 1991) and are especially suited for controlling industrial processes where only certain well known objects like product- or workpieces must be identified. Therefore the use of CAD models within the building extraction task is promosing for the search of a priori known buildings (F RStner and Sester 1989, Schickler 1992, Schickler 1993); the lack of variability makes it much more difficult to use CAD models for the extraction of unknown and complex buildings.

2.4 Generic Models for Object Recognition

A recommendable survey about methods for three-dimensional object recognition and reconstruction is given in Suetens et al. 1992. The only system using generic models for building extraction from aerial images has been described by Fua and Hanson 1987. They use simple box-type primitives linked by an object related network of relations. Among all the systems the approaches of Dickinson et al. 1992b und Bergevin and Levine 1993 are of outstanding importance: both approaches are based on three-dimensional generic object models composed of volumetric modeling primitives and on explicit modeling of the two-dimensional projective object appearances in terms of an image model. Furthermore in contrast to Fua and Hanson 1987 who only used a comparably simple image model for the primitives, both approaches utilize aspect representations of object components as the significant link between object and image modeling. They motivated our approach for building extraction and reconstruction presented in this paper.

3 GENERAL STRATEGY

In the following section we will develop a general strategy for 3D reconstruction and recognition of buildings in digital imagery based on generic CSG modeling.

Geometric modeling by combining volumetric primitives gives a representation of spatial prototypes with arbitrary structures and parameters for shape and location. On the one hand it inherits the advantages from a parametric representation of objects (as shown in 2.2) concerning the handling of object-types or -classes. On the other hand we have a generic description of objects and the whole scene consisting of its components and their relationships. This allows the recognition of objects by an active search of its parts.

Our overall concept has to consider more than the pure recognition of geometrically describable objects for two reasons. First, we want the analysis to be application specific by modeling the knowledge about the domain (see also Mayer 1993), and second, the recognition task has to be performed on natural scenes rather than sketches, that are already an abstraction containing only domain specific information.

3.1 The Role of Scene and Image Models

The overall strategy used for automated image interpretation has to meet the following requirements:

1. The deduction of the scene description from images, especially the description of scene modification, demands the explicit modeling of the scene (resp. its changes) and the expected structures in the image data either. Therefore 2D image and 3D scene structures should be as tightly-coupled as possible with respect to their formal definition and handling.
2. Scene modifications imply the need of data driven generation of hypotheses, while hypothesis verification demands model driven action. An integration of both strategies constitutes a feedback between the different processing levels.
3. Both the internal feedback between processes and the data oriented adaption of schemes make it necessary to have explicit information about the quality of results of all single processes (in the sense of a self-diagnosis) and about the model structures itselves as well. This needs adequate structures that are able to represent the model and its meta information.

Figure 1 shows the overall structure of our concept with all its internal and mutual connections between the levels of processing. The basic structure on all

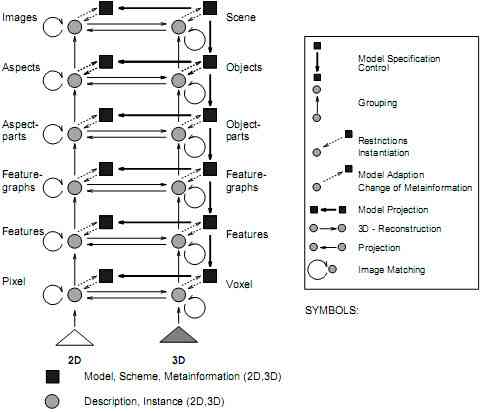
Figure 1: The overall structure

different levels is identical:

1. The 2D image model results from a formalized projection of the 3D scene model depending on projective geometry and scene illumination. The level of detail of the image model is determined on one side by the given interpretation task and on the other side by the form and quality of the extractable image structures and features.
2. Models, schemes and meta information restrict the instantiation of descriptions of 2D or 3D objects.
3. For the 3D scene reconstruction or in the case of change detection the 2D image data can be used i.e. by employing matching algorithms.
4. Knowledge about the scene can support the deduction of a scene description.
5. The deduction of image or scene descriptions or a sufficiently large number of such descriptions can be taken for further validation of the image or scene models. This serves generally for conducting the whole analysis process, in special cases it is also used for adaption or learning.

All levels correspond on the one hand to the hierarchically structured scene in the sense of a part-of hierachy, and on the other hand to the time sequential aggregation of iconic image information (pixels) step by step to more complex, thus semantically richer structures. This architecture tightly interlaces data driven and model driven processes. The starting point of the recognition is the 2D image represented by an array of pixels from which the reasoning process finally must infer a 3D scene description. The delimitation between the different levels (esp. the higher ones) is not a final one and is at this time still topic of our research.

The strategy for developing a general model, on which the interpretation operates, will consist for both the image and the object model mainly of two fundamental directions:

1. Forward modeling (top down): Starting with a scene conception in mind a 3D object model is developed, from which a 2D image model can be derived under the assumption of a projection model (see fig. 1: bold arrows).
2. Backward modeling (bottom up): Starting from existing or extracted image or object structures the process of top down modeling has to be reversed with the aim to provide the methods needed for interpretation (i.e. feature extraction, grouping and 3D reconstruction techniques).

3.2 Interpretation Model

The interpretation model defines the control strategy of the whole image analysis. It contains processing regulations for the feature extraction and for the reasoning on each single level of the image and scene model. Further it defines the communication between the modules on different levels. There are rules for this purpose defining when and in which way image resp. scene descriptions are instantiated. Another part of the interpretation model consists of rules for the extension and adaption of the model or parts of it. Since buildings may be arbitrary complex in reality, there is no chance of explicitly modeling all building variants in full detail. The reconstruction faces two fundamental problems:

1. The inverse projection of 3D objects and object parts in the 2D image space is not trivial, because the projection is not bijective. Reducing the dimension causes a loss of information, and one 2D image may originate from different 3D scenes, hence the 2D image may contain ambiguous information. This raises a classification problem, but can be overcome with the help of a priori knowledge in form of constraints and context assumptions.
2. Unavoidable Errors from the feature extraction and from occlusions or shadows on the image take effect in all reasoning steps. The uncertainty of conclusions must therefore be considered in all steps.

The coupling of the processes is established on the image side by the data driven generation of hypotheses using grouping processes. Present 3D structures are taken into account, regardless if they result from earlier observation (i.e. supplied by a GIS) or from instantaneously derived 3D hypotheses. The available image information is integrated on the actual processing level to eliminate inconsistencies and to achieve maximum accuracy of present information.

This information integration is also done on the scene side, to obtain a complete, and for each level well suited scene description.

The system has to autonomously select, with the help of stereo vision the appropriate aggregation level for the transition from image to scene description. The basis for this is built by a projection model that results from theoretical and empirical research regarding the perceptibility of objects by the artificial system. The model considers special object properties (like the geometric complexity), the projection process (esp. the illumination), the sensor properties (like the geometric resolution) and the efficiency of the available analysing methods.

The final result of the interpretation is the best-fitted scene model instance of the projected scene on the image as an approximation for the scene in reality.

3.3 Previous Approaches

Hierarchical structures for modeling images and scenes at different resolution and the close interaction of bottom-up and top-down procedures are classical concepts. Hartmann 1983 developed a hierarchical structure code based on both iconic and symbolic aggregations in a hexagonal pyramid, which is used together with the interpretation system ERNEST (Niemann et al. 1990) for interpreting industrial 2D-scenes. Andress and Kak 1987 and Lawton et al. 1987 proposed a layered representation of symbolically aggregated structures used for analysing 2D images of truely 3D scenes with explicitely providing appearance-/image models for interpretation. Strategies for interpretation still are topic of current research. Semantic networks of frames are probably the mostly used representation (cf. Niemann et al. 1990, Lawton et al. 1987) including special networks for invoking hypotheses based on previous instantiations (cf. Bruce et al. 1989). A completely different approach has been proposed by Strat and Fischler 1991 who in a cooperative way exploit multiple hypotheses using mutual ranking.

Though the results provided by the systems are quite promising an explicit modeling of the joint hierarchical structures of images (2D) and objects (3D) seemed to be missing, which is a prerequisite for a success in deriving complex 3D-structures for images.

4 THE SCENE MODEL

The scene model describes the scene that has to be recognized. It therefore must be able to project reality in a way appropriate for the application.

We distinguish between three modeling levels, which are hierarchical dependent on each other:

1. The domain model contains the semantically most meaningful part of the scene model according to the aim of the image interpretation. It describes the possible structures of the interesting objects and their possible arrangements. It is important that all objects on this level are composed of only domain specific object primitives.
2. The modeling of domain specific object primitives uses a volumetric representation. The underlying primitives for this model level are CSG primitives parametrized by additional domain specific values resp. variables. At this point the transition from modeling domain specific knowledge to pure geometric-physical modeling takes place.
3. The boundary representation of the objects (that consist of volumetric primitives) is used to derive the image model considering the geometric and physical surface properties.

Each level provides a number of parametrized primitives as a basis. These primitives can be combined to more complex structures by applying relational operators on them (i.e. the standard relations of the CSG model). Constraints are used for this task, which may be expressed i.e. in terms of predicate logic. In this case the constraints may be specified in the way defined by constraint logic programming (CLP).

4.1 Objects of the Domain Model

We are particularly interested in the domain of building reconstruction. Therefore we need semantical and structural models of the buildings of interest. But the digital images not only show buildings; instead we find multiple interactions eg. occlusions and shadows with other objects, especially with streets, vegetation etc. From this point of view a modeling of all objects possibly occuring within an observed scene might seem necessary. First of all we will concentrate on the modeling of buildings. Problems due to occlusions by other objects than buildings we will handle with special structured image modeling (see chapter 5).

In our approach buildings are defined by combinations of simple building types in the sense of object primitives as the following example shows:

The italicized components in the building definitions above (e.g. single garage, single house, two-storey family house) describe primitives of the domain modeling scheme.

4.2 Volumetric Representation of Object Primitives

The domain specific object primitives are composed of object components whose geometry and whose physical properties are represented in terms of CSG models. Indeed some object components show intrinsic functional semantics. Therefore it is possible to embed these descriptions in the next higher modeling level, but due to their predominant geometric and physical attributes it seems advantegous to postpone their semantics. Thus a sharp distinction between volumetric and domain primitives seems impossible.

For example interpreting the objects single garage and multistorey family house now as classes we derive the following decompositions in volumetric primitives:

The italicized components in the decompositions above (e. g. cuboid, vertical prism, horizontal prism) describe volumetric primitives showing pure physical and geometical properties.

4.3 Surface Representation of Object Primitives

In general we see in images only the surfaces of the observed objects. Therefore we need a transformation of combined volumetric primitives into surface-based object descriptions which includes the physical object attributes especially the spectral reflection properties guaranteeing observability. This surface representation of object primitives is the basis for the derivation of the image model.

4.4 Constraint Representation and Processing

All levels of modeling define constraints on the instances formulated on the primitive parameters and the attributes of their relations. We employ two kinds of constraints:

1. Constraints on primitives (p-constraints) define restrictions on the primitive parameter sets. Each p-constraint refers to only one single primitive.
2. Constraints on relations (r-constraints) define restrictions on the attributes of the relations between the primitives.

For example the restriction on the attribute height of the primitive storey is encoded in the following way, using the notation of the logic programming language PROLOG:

storey(floor,height).
new_house_storey(F) :- storey(F,H), H in [2.5,2.9].

The restriction on the relation angle between two faces e.g. is similarily encoded:

These constraints could be used to enforce the orthogonality between the walls and the roof of a garage:

Furthermore these constraints must generally include probabilities, probability densities or other suited ways to specify uncertainties in measurements.

5 IMAGE MODEL

5.1 Image Model Requirements

The image model provides structures for the description of images on different aggregation levels (cf. figure 1). The following requirements should be fulfilled:

1. At each aggregation level the image model should be predictable by formal derivation from the object model i.e. by deduction (1). This refers to the image structure in the form of primitives and their corresponding attributes as well as to the constraints, and to the quality measures. Using the reflectance or thereby other physical properties of the object the intensity function can be derived and in the case of CAD-objects, aspects can be deduced.
   Thus projectability (2) of a 3D object description onto a corresponding 2D image description is guaranteed. In the sense of inverting the deduction it should be possible to conclude the 3D object from its appearance in the image by abduction (3). The choice of the adequate aggregation level highly influences the performance of the reasoning process. Since an exhaustive search is not feasible in practice, hypotheses which constrain the search space best will be evaluated first.
2. The image model should be observable (4), that is, each aggregation level ought to be reachable starting at the raster level. For this purpose suitable data structures (5) should be provided.
3. The image model should be adaptive (6). Using recursive estimation new probabilities of primitives and their combinations are established by learning. In the same way this process is capable of acquiring new combinations of primitives as learned.

Example (cf. figure 2): Assuming that within the level of "parts of the objects" a normalized trihedral corner has 3 right angles ai = 90 for the corresponding aspect node the constraint Пi * cos ai < 0 can be derived (deduction). Conversely, regarding a node with condition Пi * cos ai < 0 leads to the hypothesis of being a trihedral corner in 3D (abduction). 5 of 6 unknown parameters of the mutual orientation between camera and trihedral corner can be determined (cf. Braun 1994).

The existing uncertainty of extracted features caused by occlusions and self-occlusion, bad quality of the images, etc. requires a flexible image model on different aggregation levels.

5.2 Image Model Generation

The degree of automation within image analysis mainly depends on the quality of feature extraction which transforms the iconic raster image in the form of greyvalues into a symbolic image description consisting of points, lines and regions. For the purpose of image interpretation, in addition to geometric primitives specific feature attributes and mutual relations between primitives are required to get a sufficiently informative description.

5.2.1 Aspect Graphs

Assuming all objects within the scene to be delimited by piecewise smooth boundaries, a symbolic image description can be derived using existing techniques (cf.5.3) for automatic feature extraction. Adapting to the local image structure, the only steering parameter influences the desired resolution. As feature extraction is based on a very general object model no direct support for the purpose of building reconstruction is given. For this reason the utilization of domain specific knowledge is necessary during the extraction of higher level image features.

Figure 2

Image modeling is able to satisfy these requirements by describing given objects using aspect graphs. The image model of spatial objects is represented in a graph structure with the nodes representing the different topological views (aspects) and the edges coding changes of view via nongeneric views (cf. Eggert et al. 1993). Using any matching algorithm to get the correspondence between a symbolic image description and the aspect of an object model, a proper approximation of object identification, positioning and orientation in the image can be derived.

5.2.2 Aspect Graphs based on Primitives

In accordance with modeling of buildings based on spatial primitives, generic aggregated objects are proposed to be represented using primitive based aspects (cf. Dickinson et al. 1992b). Instead of aspects of complete buildings, building-specific primitives are constructed and afterwards connected according to the object model. With regard to object recognition based on identification of parts (components) of the object, this procedure takes advantage of efficient storage and management of the aspects because the number of selected spatial primitives is small. Above all, this form of aspect representation is not dependent on the number of possible parts. Within the context of building reconstruction this point of view is of remarkable importance since architecture shows a large variety of forms and mixed forms not only within single houses, but also within complex clusters of houses.

5.2.3 Aspect Hierarchy

Finding and evaluating hypotheses about objects and object parts causes problems due to occlusions and lacking or irrelevant information of the feature extraction. In order to cope with these problems, we, extending the approach of Dickinson et al. 1992a suggest a hierarchical aspect representation, extended to all possible feature primitives, that is besides regions, also points and lines.

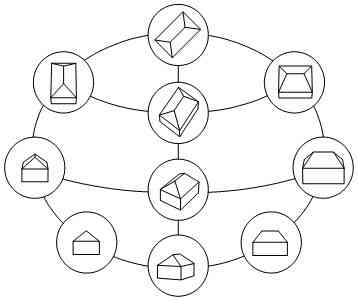
Figure 3

Figure 4

The highest aspect level consists of the entire aspect of given spatial primitives. Due to occlusions only parts of the object are visible. Therefore the second level represents regions, points and lines which contain primitive based aspects. Finally the lowest level within that hierarchy provides different configurations of boundaries which contain aspects of parts of the next level.

The connection of different levels is given by conditional probabilities expressing the knowledge of the relation of an aspect unit to the next higher representation level.

5.2.4 Representation of Aspects of Primitive Combinations

To effectively exploit relations between extracted feature primitives (points, lines, regions) reference to aspects of single object primitives is not sufficient. Significant feature relations not only appear within features of single primitive aspects, but rather between features of neighboring primitives; for example, between features between the primitive "floor" and the primitive "roof. For this reason expanding the aspect representation for single primitives to pairs of primitives is useful. Image modeling therefore not only contains single spatial primitives but also the representation of pairs of primitives. One could expand further to three and more primitives, however, additional effort in the representation and in the search on the one hand and realized gain on the other hand must be compared.

For example, figures 3 and 4 show the aspect graph for a combination of two primitives floor { hip-roof and for one selected aspect, the aspect hierarchy containing relations between the feature classes regions (a), lines (b), and points (c).

5.3 Generation of an Image Description

One crucial step within image interpretation is the matching of the observed image, represented by any adequate image description, with a corresponding symbolic object description in the form of an object model. Therefore feature extraction is the first step in image analysis and aims at replacing the image by a suitable representation, here a symbolic image description.

5.3.1 Characteristics of Digital Images

The content of the observed image mainly depends on the original 3D scene and on the sensing process. For this reason feature extraction requires the setting up of models of the scene to be recovered and of the sensing process used for observation called the observation model.

The following scene model, though involving no semantic knowledge, seems to be complex enough to implicitely cover the geometry and physics of a large class of scenes. We assume the scene to have the following properties:

1. The objects are geometrically and physically bounded.
2. The objects are neither transparent nor reflecting.
3. The boundaries of the surface patches consist of piecewise smooth patches.
4. The albedo function of the scene consists of piecewise smooth patches.
5. The boundaries of the albedo patches consist of piecewise smooth boundaries.

The image model depends on the observation model which can be represented by the following 3 steps of the imaging process:

1. The ideal continuous image f(x;y) results from projecting the scene with a camera modeled as a pinhole camera. The lighting is di ~ use and the light sensitive area is of unlimited resolution. The image area I therefore consists of homogeneous segments S, which are assumed to show piecewise smooth boundary lines L. Points P are either boundary points of high curvature or nodes where three or more regions meet.
                (1)

Besides the extracted image primitives the segmentation also contains relations between primitives (cf. figure 5a).

2. Assuming a real objective, more general lighting condition and a light sensitive area of limited resolution, projection yields a real continuous image f(x;y). Generally this leads to continuous blurred images, with the blurring being nonhomogenious and anisotropic.
   We obtain segment-regions S, often referred to as blobs, point-regions P and line-regions L, lines and points lying inside the corresponding regions. Similarily to 1. the image area I can be similarily partitioned into three parts S, L and P (cf. figure 5 b.).
3. The digital image g(r; c) is a sampled and noisy version of the real continuous image: g(r;c) = f(r;c) + n(r;c). The noise is mainly caused by the Poisson- process of photon flux, by the electronic noise of the camera and - in case g is rounded to integers - by the rounding errors.

Figure 5: shows the structure of the ideal image (a.) with points, lines (edges), and segments as basic features and of the real image (b.) containing point-, line- and segment-type regions. (c.) shows the classification tree for image features

Assuming these specified properties of the digital image, feature extraction thus allows to recover the position of points, lines and regions and the mutual relations between these features primitives in order to obtain a relational description in the sense of a feature adjacency graph (cf. figure 6 c), which can serve as a structural image description for further processing steps.

5.3.2 Extraction of Feature Primitives and their Mutual Relations

Referring to the presented model of the digital image a symbolic image description can be derived, consisting of points, lines and regions.

For the purpose of feature destinction the local image characteristics of the intensity function can be used (FoRSTNER 1994). Convolving the squared gradient with the rotationally symmetric Gaussian function Ga(x;y) with centre and standard deviation a leads to the average squared gradient which describes the local structure of the intensity function. After diagonalization of the matrix Tog leading to the eigenvalues A1 (g), A2 (g) features can be derived in several steps:

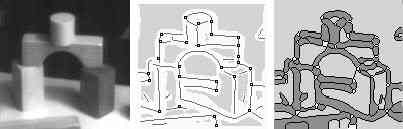
Figure 6: shows the recovery of the image structure with the proposed procedure. The pixels of the original image (a.), the extracted feature primitives (b.) and the exoskeleton of the features, which allows deriving the mutual relations between the primitives (c).

1. subdivision into homogeneous and nonhomogeneous regions: Comparing the trace h = trTg = \1 (g) + 2 (g) for measuring the homogenity with a threshold T h (cr) enables the distinction of segment-regions on the one hand and line and point regions on the other hand.
2. classification of line and point regions: Investigating the ratio v = A2 =A1 of the eigenvalues yields the degree of orientation or of isotropy. Using a second threshold T (??) on v results in line- and point-regions.

The thresholds T (??) can be put into relation with the image noise characteristics, the width a of the Gaussian kernel Ga and a significance level of a y2 -distributed test value. The threshold T (??) can be fixed for all applications, e.g. to 0.1.

Using this classification of point and line regions a precise localization of point and line features inside their corresponding feature regions can be achieved (cf. figure 5 c).

In addition to the extraction of feature primitives, relations between those features can be derived using the exosceleton of homogeneous and nonhomogeneous regions. A feature adjacency graph serves for representation of the relations (Fuchs et al. 1993).

Because the proposed approach for fully automatic feature extraction is related to a coherent theory, consistency of the symbolic image description is guaranteed. It enables a quantitative evaluation which is fundamental during interpretation using different features simultaneously. In figure 6 we show the results of the proposed procedure for feature extraction.

For the purpose of grouping into semantically more significant image descriptions, the feature adjacency graph can be further evaluated using the image models as described in chapter 5.2. This is the first step within the reasoning process depending on any object model.

5.3.3 Restrictions onto Observation Space

Terrestrial as well as aerial images are characterized by specific restrictions concerning the observed space. For example, within aerial images the space is restricted to the upper cone of the observation sphere. Further restrictions concerning the projection model result from the actual observation condition; for example, paral-lelprojection is a locally adequate model and for aerial images, taken from great height the nadirpoint can be considered to be the only vanishing point.

In general, during one and the same flight the orientation parameters are known and the image scale is considered to be fix.

This additional information provides helpful constraints which facilitate establishing hypotheses within recognition and reconstruction.

6 CONCLUSION

We have presented a generic approach for the modeling of buildings within an overall concept for three-dimensional scene reconstruction based on the interpretation of digital images. The overall concept shows different levels of modeling and processing. These levels reflect the hierarchical scene modeling in the sense of a part-of hierarchy as well as the successive aggregation of the iconic image information into more complex structures. Our concept reveals well defined levels of object and image modeling, and presents itself as a framework for the implementation of different interpretation strategies.

The development of our concept is still in the beginning. The feature extraction, some procedures for matching and reconstruction on the feature level as well as for objective parameter estimation are complete. Methods for texture based image segmentation and for the verification of 3D-hypotheses can be adapted from computer graphic methods. Currently we are investigating and developing on

1. the observabiliy of object details,
2. the quality of feature graphs in dependency on noise and scale space,
3. the grouping of image faetures,
4. constraints on simple building types,
5. the aspect modeling of building primitives and pairs of building primitives and
6. the formalization of the transformation from 3D constraints to 2D constraints.

Especially we have to consider the integration of logical and statistical, i.e. strong and weak constraints as well as the classification of domain objects in the highest level of modeling. Medium-term aims are the integration of all modules and the inclusion of non-building objects, especially of roads and vegetation.

Acknowledgements:

This work largely was done within the project \Semantic Modeling and Extraction of Spatial Objects from Images and Maps" especially in the subproject \Building Extraction" which is supported by the Deutsche Forschungsgemeinschaft. We thank the DFG for supporting our work.

References

1. Andress K.M., Kak A.C. (1987): A Production System Environment for Investigating Knowledge with Vision Data. In: Kak, A.; Chen, S. (Eds.), Spatial Reasoning and Multi-Sensor Fusion, pages 1{12. Morgen Kaufmann, Inc., 1987.
2. Bergevin R., Levine M. L. (1993): Generic Object Recognition: Building and Matching Coarse Descriptions from Line Drawings. IEEE T-PAMI, 15(1):19{ 36, 1993.
3. Braun C. (1994): Interpretation von Einzelbildern zur Gebaudeerfassung. PhD thesis, Institut fur Photogrammetrie, Universitat Bonn, 1994.
4. Bruce A., Draper R.T., Collins J.B., Hanson A.R., Riseman E.M. (1989): The Schema System. IJCV, 2(3):209{250, 1989.
5. Chiou R., Hung K.-C., Guo J.-K., Chen C.-H., Fan T.-I., J.-Y.Lee (1991): Polyhedron Recognition Using Three-View Analysis. Pattern Recognition, 25(1):1{16, 1991.
6. Clowes M. (1971): On Seeing Things. Artificial Intelligence, 2:79{116, 1971.
7. Dickinson S., Pentland A., Rosenfeld A. (1992): 3-D Shape Recovery Using Distributed Aspect Matching. IEEE T-PAMI, 14(2), 1992.
8. Dickinson S., Pentland A., Rosenfeld A. (1992): From Volumes to Views: An Approach to 3D Object Recognition. CVGIP, 55(2):130{154, 1992.
9. Eggert D., Bowyer K., Dyer C., Goldgoff D. (1993): The Scale Space Aspect Graph. IEEE T-PAMI, 15(11), 1993.
10. FORSTNER W., Sester M. (1989): Object Location Based on Uncertain Models. In: 11. DAGM-Symposium, Hamburg, 1989.
11. FORSudh W. (1994): A Framework for Low Level Feature Extraction. In: Ek-LN, J.-O. (Ed.), Computer Vision, ECCV '94, Vol. II, pages 383{394. Lecture Notes in Computer Science, 801, Springer-Verlag, 1994.
12. Fua P., Hanson A.J. (1987): Resegmentation Using Generic Shape: Locating General Cultural Objects. Pattern Recognition Letters 5, pages 243{252, 1987.
13. Fuchs C., Lucherbach Th., Pan H.-P., Furstner W. (1993): Land Use Mapping from Remotely Sensed Images. In: Colloquium an Advances in Urban Spatial Information and Analysis, Wuhan, China, 1993.
14. Hansen C, Henderson T.C. (1989): CAD-based Computer Vision. IEEE T-PAMI, 11:1187{1193, 1989.
15. Hartmann G. (1983): Erzeugung und Verarbeitung hierarchisch codierter Kon-turinformation. In: 5. DAGM Symposium, VDE-Fachberichte 35, pages 378{ 383, 1983.
16. Herman M., Kanade T. (1987): The 3D MOSAIC Scene Understanding System: Incremental Recognition of 3D Scenes from Complex Images. In: Fis-chler/Firschein (Ed.), Readings in Computer Vision, pages 471{482. Kauf-mann, 1987.
17. Heyden A. (1994): Consistency and Correction of Line-Drawings, Obtained by Projections of Piecewise Planar Objects. In: Ecklundh, J.-O. (Ed.), Computer Vision, ECCV '94, Vol. I, pages 411{419. Lecture Notes in Computer Science, 800, Springer-Verlag, 1994.
18. Huffman D. A. (1971): Impossible Objects as Nonsense Sentence. Machine Intelligence 6, pages 295{323, 1971.
19. Kanatani K. (1990): Group-Theoretical Methods in Image Understanding. Springer-Berlin, 1990.
20. Lang F., Schickler W. (1993): Semiautomatische 3D-Gebaudeerfassung aus digitalen Bildern. Zeitschrift fur Photogrammetrie und Fernerkundung, 5:193{ 200, 1993.
21. Lawton D.T., Lewitt T.S., McConell C, Glicksmann J. (1987): Terrain Models for an Autonomous Land Vehicle. In: Fischer; Firschein (Eds.), Readings in Computer Vision, pages 483{491. Kaufmann, 1987.
22. Lin C, Huertas A., Nevatia R. (1994): Detection of Buildings Using Perceptual Grouping and Shadows. In: Proceedings CVPR `94, Seattle, Washington, pages 62{69, 1994.
23. Lin C.L., Zheng Q., Chelappa R., Davis L.S., Zhang X. (1994): Site Model Supported Monitoring of Aerial Images. In: Proceedings CVPR `94, Seattle, Washington, pages 694{699, 1994.
24. Liu C.-H., Tsai W.-H. (1990): 3D Curved Object Recogmition from Multiple 2D Camera Views. CVGIP, 50:177{187, 1990.
25. Mayer H. (1993): Automatische wissensbasierte Extraktion von semantischer Information aus gescannten Karten. PhD thesis, Fakultat fur Bauingenieur -und Vermessungswesen , Technische Universitat Munchen, 1993.
26. McKeown D.M. (1990): Towards Automatic Cartographic Feature Extraction from Aerial Imagery. In: Ebner. Fritsch, Heipcke (Ed.), Digital Pho-togrammetric Systems. Wichmann-Karlsruhe, 1990.
27. Niemann H., Sagerer G., Schroder S., Kummert F. (1990): Ernest: A semantic network system for pattern understanding. IEEE T-PAMI, 12:883{ 905, 1990.
28. Quam L., Strat Th. (1991): SRI Image Understanding Research in Cartographic Feature Extraction. In: H. Ebner, D. Fritsch, Ch. Heipke (Ed.), Digital Photogrammetric Systems, pages 111{121. Wichmann, Karlsruhe, 1991.
29. Schickler W. (1992): Feature Matching for Outer Orientation of Single Images Using 3-D Wireframe Controlpoints. In: Internat. Archives for Photogramme-try, B3/III, Washington, pages 591{598, 1992.
30. Schickler W. (1993): Towards Automation in Photogrammetry. Geodetical Information Magazine, 7(4):32{35, 1993.
31. Steinhage V. (1993): Verdeckungen und spezielle Sichten bei der Rekonstruktion von Polyederszenen. Infix-Verlag, 1993.
32. Strat T.M., Fischler M.A. (1991): Context-Based Vision: Recognizing Objects using Information from Both 2-D and 3-D Imagery. IEEE T-PAMI, 13(10):1050{1061, 1991.
33. Suetens P., Fua P., Hanson A. J. (1992): Computational Strategies for Object Recognition. ACM Computing Surveys, 24(1), 1992.
34. Sugihara K. (1986): Machine Interpretation of Line Drawings. MIT-Press, 1986.
35. Waltz D. L. (1975): Understanding Line Drawings of Scenes with Shadows. In: Winston, P. H. (Ed.), Psychology of Computer Vision, pages 19{91. McGraw-Hill, New York, 1975.