Kolbe T. H., Groger G. TOWARDS UNIFIED 3D CITY MODELS

An increasing number of municipalities decide nowadays to build up 3D city models. Often the main purpose of such a model is to support urban planning processes. However, in most cases this support currently is restricted to the visualization of virtual scenes. The first reason is that there are still no commercial 3D geoinformation systems available. Thus, city models typically are implemented on top of CAD systems or visualization software which all offer only limited modeling capabilities. The second reason is that there does not exist a standard for 3D city models yet. Only few investigations about multifunctional and multiscale modeling, storage and analysis have been carried out so far. In this paper we propose a unified model for the representation of spatial objects in 3D city and regional models. It constitutes a base schema providing patterns for application specific 3D models. It is shown how real world objects are represented by features with geometric, topological and thematic (i.e. non-spatial) properties. We explicitly cope with the problem of multiscale representations. A special level-detail-of-relation between features and their geometry is introduced ensuring spatial consistency between 3D models at different scales. Furthermore, issues concerning the integration of features below surface with the digital terrain model are discussed. Finally, we show how interoperability at system level can be achieved by mapping the proposed model to GML3, the new standard for the representation and exchange of spatial data developed by the OpenGIS Consortium.

In the context of growing spatial data infrastructures one major issue is the interoperability of systems and data (Groot & McLaughlin, 2000). Different systems, formats and conceptual models prevent the immediate combination of distributed spatial information available at different locations. For example, if a disaster management system should monitor a flooded region affecting multiple cities, it has to have access to the spatial data of each municipality involved. Furthermore, the system must know how to interpret each data set in order to determine the endangered buildings. Due to the variety of different existing models this approach is infeasible. Generally, this problem arises in all application scenarios that require analysis or visualization of large areas, where 3D models from different authorities or data providers have to be integrated. Due to Bishr, interoperability problems can be overcome by specifying common models and structures on the semantic, the schema and syntactic level (Bishr, 1998).

In the Special Interest Group “3D” (SIG 3D) of the initiative “Geodata Infrastructure North Rhine-Westphalia” (GDI NRW*) municipalities, scientists and software developers work together on the development of a unified approach for 3D city models. The modeling schemes presented in this paper are developed based on discussions within this group (Groger & Kolbe, 2003). The aim is to obtain a multifunctional 3D city model which can be used for analysis and simulation purposes as well as for visualization. It should be a core model in the sense that specific applications like 3D cadastre or facility management can be built on top of it.

Generally, a spatial core model has to offer means to maintain spatial integrity. Thus, not only geometry but also topological aspects have to be considered. Furthermore, the model must offer possibilities for a differentiated representation of real world objects regarding both their thematic and spatial structures. This includes the definition of complex object types by aggregation and specialization.

Often, spatial data are collected at different scales. For example, a municipality may have a complete small scaled, coarse 3D city model on the one hand and detailed representations of selected buildings on the other hand. A problem that is typical for 3D city models is, that users want to mix objects from different scales for efficient visualization or to use the highest detailed representation available within analysis tasks (Koninger & Bartel, 1998; Coors & Flick, 1998; Zipf & Schilling, 2003). In both cases it has to be ensured that no spatial object is considered or counted twice or more. To enable automatic consistency checking, the relations between the spatial representations of an object at different scales have to be made explicit.

In addition to objects above surface, cities typically show a variety of underground structures, e.g. pedestrian underpasses, tunnels, and subways which have been neglected both in theory and practice of 3D gis and 3D city models so far. For new applications like pedestrian navigation and disaster management or highly detailed visualizations the support of underground structures is essential. Here, the main problem is the interface between subsurface spatial objects, the digital terrain model and objects above surface.

To reach interoperability on the system level, syntactic compatibility has to be achieved. The OpenGIS Consortium has ecently proposed the third version of their Geography Markup Language GML3, which will be the most important standard to encode 2d, 2,5d, and 3D spatial objects in the future. We discuss how our model can be mapped to GML3 and hint at conceivable problems regarding the capabilities of GML3.

The rest of the paper is organized as follows: Section 2 presents the geometric-topological base model and shows how it can be used to represent real world objects, including hierarchical aggregations. The consistent management of different geometrical representations of spatial objects is explained in section 3. The following section deals with subsurface objects and their integration into 3D city models. The mapping of the proposed model to GML3 is discussed in section 5. Finally, results are summarized and open questions are addressed.

In literature many conceptual models for 3D objects have been proposed. If spatial integrity has to be maintained and redundant storage of object geometries should be avoided, geometric- topological models are preferred (Oosterom et al., 2002; Zlatanova, 2000; Plumer & Groger, 1997; Molenaar, 1992). The developed concepts became established in the ISO 19107 standard for the representation of geometry and topology of spatial objects (Herring, 2001). Whereas this standard offers a multitude of modeling options, it seems to be too complex if only certain aspects are needed. Therefore, we propose a model that is based on ISO 19107, but is more compact and easier to handle.

The Abstract Model of the OpenGIS Consortium represents spatial objects by features (OpenGIS Consortium 1999). Features are abstractions of real world objects resp. phenomena having spatial and non-spatial properties. Like in GML we distinguish betwen the base model and application specific modeling. The base model defines the basic 3D primitives and provides the modeling mechanisms that are needed for any application specific 3D model. Therefore, it has to be open for different application scenarios like 3D cadastre, facility management etc. It also has to be flexible in the sense that it can represent already existing 3D city models.

The base model consists of the geometric-topological model on the one hand and the thematic model on the other hand. The former is further divided into the primitive level and the aggregation level (see fig. 1). This structure allows for the coherent modeling of both spatial and thematic differentiations. For example, if the thematic aspects of spatial objects are further differentiated by specializations or aggregations, spatial properties may be associated with thematic aspects at any level.

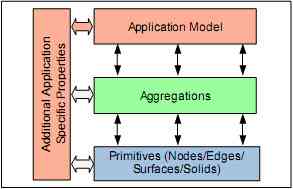
Figure 1. Structure of the base model. An application model comprises thematic and spatial aspects, where the latter may be represented by simple or aggregated primitives.

The core of the data model is built by the geometric-topological modeling of 0-, 1-, 2-, and 3-dimensional primitives in the form of a point, edge, surface, and volume model. Since any higher dimensional primitive is composed of primitives of the next lower dimension, only nodes (0 dim.) have explicit coordinates. Whereas the geometry of all other primitives is defined implicitly, topology between the different primitives is explicit. Edges are defined by a start and an end node. Surfaces are bounded by an outer ring, which is an ordered set of edges. Holes inside a surface are bounded by inner rings. Volumetric objects are called solids and are modeled using the boundary representation schema (B-Rep, see Foley et al., 1995), which is a set of at least 4 surfaces that has to be closed, i.e. there must not exist a path from the interior to the outside without having to break through a surface. Each surface of a solid is oriented to distinguish between inside and outside. Figure 2 shows the UML diagram (Booch et al., 1997) for the primitives.

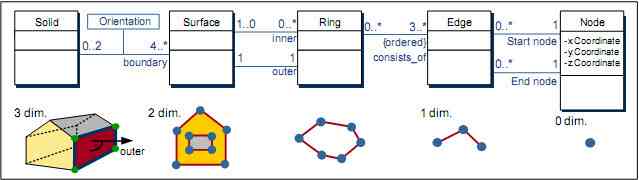
Figure 2. Geometric-topological model for 0-, 1-, 2-, and 3-dimensional primitives.

The aggregation level is built on top of the primitive level. It contains a recursive aggregation schema for every primitive type. This aggregation schema allows the definition of nested aggregations. For example, a building can be composed of the house and the garage, while the house itself may be built by a roof object and the house body (see fig. 3).

Figure 3. Composition of complex vol umetric objects by recursive aggregation of solids. Touching solids share common nodes, edges, or surfaces (the latter case is shown above).

To avoid redundancy and to maintain explicit topological relations between parts of the aggregate, touching surfaces must be represented only once and must be referenced by each part. As can be seen from the lower part of fig. 3, this requires partitioning of the respective surfaces. B-Rep only considers visible surfaces. However, to make topological adjacency explicit and to keep the possibility to delete one part of a composed object without leaving holes in the remaining aggregate, we propose to include the touching elements. Whereas touching is allowed, permeation of objects is not in order to avoid the multiple representation of the same space.

The aggregation of surfaces is similar to the aggregation of solids. Surface geometry objects consist of single surfaces or a (recursive) aggregation of surfaces, where the orientation of each surface wrt. the aggregate has to be specified. Using the notion of surface aggregates, triangulated irregular networks (TINs) are defined as a special case. The TIN consists of triangles which are specialized surfaces having exactly 3 edges. Figure 4 shows the UML diagram for surface geometries.

Figure 4. Surface geometry objects can be single surfaces or a (recursive) aggregation of these. A triangular irregular network (TIN) is a special surface aggregate consisting only of triangles.

The geometry superclasses Solid Geometry, Surface Geometry, Line Geometry, and Point Geometry build the interface to any application specific model. Spatial objects are first modeled wrt. their semantic properties and structures, i.e. part-of- and is-a-hierarchies. Then spatial properties are expressed by associations with the corresponding geometry classes of the base model. For example, most objects of a city could be subsumed under a class Objects-above-Surface (“Surface Object”). Generally, to express the spatial reference of thematic objects their superclasses are associated with the superclass Object Geometry. In our example, a building would be modeled as a thematic specialization of a Surface Object. To differentiate the spatial properties, the Building class may be associated with more specific geometry classes. Figure 5 shows the UML diagram for the given example. Thematic properties of buildings would be modeled as attributes of the corresponding class. Buildings could also be further differentiated into e.g. industrial complexes, residential or public buildings by specialization. Further object types like bridges, monuments and vegetation could be modeled in a similar way as subclasses of Surface Object. Each class would be associated with the appropriate geometry classes.

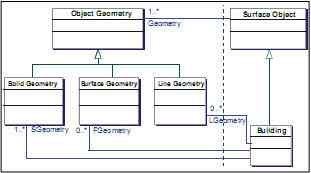
Figure 5. Example for a (minimal) application specific model. Buildings are special objects above surface and must have at least one solid geometry and may have extra surface and line geometries.

The concepts presented in the previous sections allow the representation of a feature by only one geometry object. Many applications of 3D GIS, however, require the management of several representations of one object simultaneously, describing different levels of detail (LoD). Traditionally, the main reason for representing different LoD is efficient visualization (Koninger & Bartel, 1998; Foley et al., 1995; Guthe & Klein, 2003). Efficient analysis is another important reason for using LoD in a multifunctional 3d GIS. For example, counting the number of buildings in a city can be performed most efficient by considering the buildings on a less detailed level. Beside efficiency, limited availability of data is an additional reason for managing LoD. Often highly detailed data is available only for some selected, small regions, while less detailed data covers the whole area of interest. In such a situation, a procedure performing an analysis should use the coarser data only where detailed data is not available, and the detailed data otherwise to be as precise as possible.

The crucial point in managing different LoD is to ensure that for each object – although it is represented at different levels of detail – only exactly one level is considered when performing an analysis or visualizing data. The set of representations of objects, which can be analyzed or visualized together safely, is called a view**. Note that a view may contain objects from different LoD, but it never may contain the same object or the same part of space more than once. Otherwise, a wrong visualization is obtained, e.g. the same building is displayed twice. A wrong result of an analysis may be a consequence of considering the same object more than once, e.g. for counting the number of buildings in a district, only one representation of each building should be considered, not two or more.

The main difficulty in managing LoD to obtain consistent views stems from the fact that the relationships between the representations at different levels may be very complex. We have identified three cases, which cover all possible relationships:

In the following, we discuss all three cases separately. We give examples, show how to model each case using UML, and present consistency constraints for views which prevent multiple representations of the same part of space.

In the first case, one object has a single representation in all LoD. An example is depicted in Figure 6, where one building has a representation as a simple block in LoD1, as a textured object with a simple roof in LoD2 and as a highly detailed object with complex roof shape, detailed windows, entrances and ledges in LoD3. The corresponding UML instance diagram*** is given in fig. 7a), where a thematic object Building X has three relationships to different solids representing its geometry properties. In our example, the instance Solid Geometry1 corresponds to the simple block in Fig. 6, Solid Geometry2 corresponds to the LoD2-representation and Solid Geometry3 to LoD3 in Fig. 6.

Figure 6. One building has three representations in different LoD.

The UML class diagram in fig. 7b) generalizes the instance diagram by representing the thematic class Building and its relations to the geometric class Solid Geometry. Note that the names of the associations between thematic objects and geometry objects, e.g. LoD1-Geometry, are qualified and have specific semantics. Qualified means that the names are constructed according to the schema LoDX-Geometry, where X ? {0, 1, 2,…} is an integer which indicates the LoD level. The semantics of this association is that it assigns a LoD-Geometry of the respective level to a thematic object.

This semantics is used by consistency constraints, which have to be formulated and maintained to prevent modeling the same object twice. The first case is simple: the constraint states that for each thematic object, there exists exactly one LoD- Geometry-relation to a geometry object.

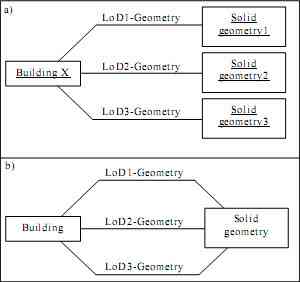
Figure 7. Illustration of the first case. A building has one representation in each LoD. Fig a) shows the instance diagram, while the corresponding class diagram is depicted in b).

Often objects which are identifiable in one LoD are merged together in a less detailed LoD. An example for this second case of relationships between LoD is shown in fig. 8a), where a aggregation hierarchy between a street block, four street rows and nine buildings exists. Each building belongs to exactly one row, and each row to exactly one block. The instance diagram of this scene forms a tree; it is depicted in fig. 8 b). An abstract model of this second case is shown in fig, 8c), where the hierarchical structure between the three levels is represented by a qualified aggregation called LoD-Aggregation. Its semantics is that it aggregates thematic objects in different LoDs spatially.

The consistency constraint for views, which ensures that no object is considered twice, is as follows:

successor in the tree is defined recursively, i.e. A is successor of B if there is a path downward the tree connecting B and A.

To illustrate the consistency constraint, we consider the aggregation tree in Fig. 8a). If the representation Block is in a view, no other representation is allowed to be contained in this view, since all other are successors of Block in the tree. Similarly, Row1 and Building 2 may not be in the same view. Row1 and Building 4 to Building 9 may be in the same view, since there is no successor relation between both sets.

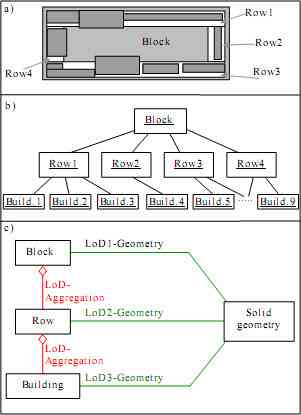
Figure 8. Illustration of the second case, where the LoD form a hierarchy. Fig. a) depicts a scene with one block (gray), four rows (white) and nine buildings. The corresponding instance diagram is given in b), while Fig. c) shows the UML diagram.

Due to independent data collection, a hierarchical relation between LoD may be missing. For example, in the scene shown in fig. 9a) Districts and Rows both have a hierarchical relation to Buildings, but there is no such relation between Districts and Rows. Unlike the second case, the structure of this scene is not a tree, but a directed acyclic graph, abbreviated dag (Cormen et al., 1990). It is depicted in fig. 9b). In the dag, the direction of the edges is downward from a lower to a higher, i.e. more detailed LoD. The UML class diagram, which models this scene, is given in fig. 9c). Note that there is no aggregation association between the classes District and Row. Again this is a qualified aggregation with the same spatial aggregation semantics as in the second case.

The view consistency of a scene represented by a dag is guaranteed by the following constraint:

Similar to the definition for trees, a successor in the dag is given recursively by traversing the directed edges downward. Referring to the example given in fig. 9 a) and b), District A and District B may be in the same view, since both have no common successors. The same is true for District A, Building 2, and Building 6. District B may not be combined with Row 2, since both have a common successor Building 6.

Note that the constraint derived for the second case is a logical consequence of this consistency constraint: If A and B have no common successors, there is no successor relation between A and B or B and A. In a tree, if two representations A and B have a common successor, it must A or B, since no representation has more than one predecessor.

Figure 9. Illustration of the third case, where no hierarchical relation between all levels exists. Fig. a) depicts a scene with two districts (dark gray and light gray), two rows (white) and six buildings. The corresponding instance diagram is given in b), while Fig. c) shows the UML diagram.

section 2 the spatial aggregation between features and its parts, for example between a building and its walls, was considered and modeled using UML. The LoD-Aggregation presented in the last section has different semantics, albeit both have a specific spatial meaning. Of course, both kinds of spatial aggregation may occur in combination. An example is given in the UML class diagram in fig. 10, which will be discussed in the following. On one hand, a Block is a part-whole aggregation of Walls, and a Building is a part-whole aggregation of a Footprint and Wall resp. Roof-Surfaces. Each of both aggregations occurs in one single LoD. On the other hand, there is a LoD-Aggregation relating Blocks and Buildings, which is between different LoD.

To guarantee consistency of a view combining both types of aggregation, two kinds of constraints have to be employed. The first states that all objects involved in a part-whole-aggregation always have to occur together in a view. The second type of constraint ensures that objects from different LoD are never considered together; corresponding rules were already presented in the last section and have to be extended accordingly.

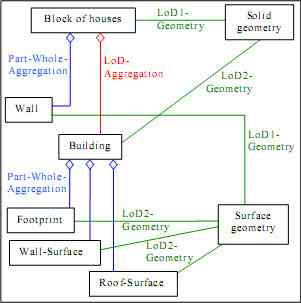
Figure 10. Combination of part-whole-aggregations (blue) and a LoD-aggregation (red) in one single UML model.

In the context of computer graphics, the LoD concept is used to derive efficient visualizations from highly detailed data. Only the detailed data is stored, while the coarser LoD are generated automatically by simplification (Foley et al., 1995; Guthe & Klein, 2003; Coors, 2001). In GIS, the situation is different, since the representations of an object are collected and stored independently. For example, data about a building can be yielded by constructing using CAD software, by ground measurements, or by evaluating aerial photos. Thus in GIS, the main problem is to manage several representations consistently, not to derive less-detailed from detailed data.

The problem of deriving the relationships between different LoD, which are collected independently, is discussed in (Sester et al., 1998; Zipf & Schilling, 2003). These approaches are complementary to ours, since we focus on the consistent management of the relationships, not on their derivation.

The management of different LoD is discussed in (Coors & Flick, 1998) in the context of visualization only. This approach is, however, restricted to the first simple case presented in this section, where one feature has representations in different LoDs. The other more complex aggregation cases are not discussed. (Koninger & Bartel, 1998) present examples for hierarchical aggregations, but they do not differentiate between part-whole- and LoD-aggregations. The management of the second case, the hierarchical aggregation, is dealt with in (Vangenot, 2002), but the third case and the combination of the different kinds of aggregations are not taken into account.

In addition to features above the surface, subsurface objects like unnels or pedestrian underpasses are essential for multifunctional city models. When considering such objects, wo additional problems arise. First, it is not obvious how to choose the appropriate geometry type for subsurface objects. While for objects above surface their enclosed volume is repre- ented, for subsurface objects the hollow space has to be modeled. The ISO Standard 19107 (Herring, 2001) denotes a hollow space that lies within a solid a shell. However, since this hell must be completely encapsulated, i.e. it must not have a connection to the outside of the solid, it is not a suitable concept for the representation of man-made underground tructures. Due to the fact, that these hollow spaces must have been constructed and accessed from the outside, they neces- arily must have an entrance resp. exit.

The second problem when modeling subsurface objects is their ntegration with the DTM. On the one hand, there must be holes n the DTM to reach underground areas. On the other hand, DTMs are tessellations covering the represented area completely without holes (Okabe et al., 1992).

Now, when integrating DTM and underground objects, the first aim is to ensure that no gaps between the DTM and the ubsurface structures occur at the entrances. This can be achieved by employing a constrained (delaunay) triangulation Okabe et al., 1992), where the edges of the subsurface objects hat touch the surface also become edges of triangles of the DTM. These edges are shared by the DTM and boundary faces of the underground objects.

The answer how to model the hollow space depends on the decision wether to cut holes in the DTM or not. If the triangles of the constrained triangulation that cover the entrance are emoved, then the subsurface object should be ‘opened’ as well n order to get access from the outside. However, because the ubsurface structure is open, it cannot be represented by a solid. nstead, it must be modeled as a set of (oriented) surfaces. The advantage of this approach is that visualization is traightforward (see fig. 11a).

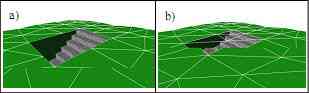
Figure 11. Entrance to a pedestrian underpass and its inte- gration with the DGM. In Fig. a), a hole is cut into the DTM, while in b) “invisible” triangles of the DTM cover the entrance.

The drawback of the approach is that DTMs loose their cover- ing property and that subsurface structures cannot be represen- ted by solids. The latter makes it difficult to compute the volume of hollow spaces which may be of interest for specific analysis tasks like the simulation of the consequences of flooding. To preserve the covering property of the DTM and the solid property of subsurface objects, we suggest that every underground object must be bounded upwards by the DTM. The triangles that cover the entrance then are shared by the DTM and the solid representing the underground object. The triangles are marked as “invisible” and can be left out in visualizations (see fig. 11b).

To ensure interoperability on a syntactical level, open, vendor- independent standards have to be employed. The Geography Markup Language GML (Cox et al., 2003), which was released by the Open GIS Consortium recently, is expected to become the most important standard for interchanging GIS-data in the future. To employ GML3, we have to make sure that the proposed model can be mapped to GML3 completely. In particular, we have to check the following aspects:

The representation of thematic objects and attributes in GML3 is straightforward, since it allows objects with arbitrary attributes and relations, as well as their (thematic) aggregation and generalization. The GML3 representation of topology and geometry is based on the standard ISO 19107 Spatial Schema (Herring, 2001), which is quite similar to our model. The concept of recursive aggregation at a geometrical level is included in this model, too. One main difference is, that Spatial Schema differentiates between topology and geometry objects, while in our model both aspects are merged. However, this problem can be solved by adopting the Simple Topology model, which is defined in (Herring, 2001). It just has to be extended from 2D to 3D to handle solids adequately.

In GML3 the relation between thematic features and geometry is realized by so-called Geometry Properties. For one feature, the number of such properties is not restricted. Furthermore, the name of such properties may be user-defined, and it can be related to homogenous geometry types. Thus the level-of-detail concepts, which were introduced in the previous section, can be implemented using GML3.

In our model, graphical properties have to be assigned to single features as well as to all features belonging to a class. Both provides GML3, since its Style Properties may be assigned to single features or to whole classes. Furthermore, Parameterized Styles enable graphics, which depend on concrete attribute values. Styles may be symbolic, i.e. colors for point, line, or area objects, or individual textures. The style concept used in GML3 is based on the graphical language SVG (Scalable Vector Graphics) (W3C, 2002). This implies an important restriction: the shape of individual textures or images must be rectangular. In a 3D city model, however, textures may be shaped arbitrarily. In addition, SVG is a 2D language. Thus the placement of individual textures on a 3D surface may cause problems.

In summary it may be said, that GLM3 is suitable to represent standardized 3D city models. It just has to be supplemented by methods to handle textures adequately.

The developed base model defines a framework for the representation of 3D city models. It is more compact and easier to understand than the ISO 19107 standard. Nevertheless, it has strong modeling capabilities and also allows to maintain geometric-topological consistency. It is easy to implement on top of relational, object-relational and object-oriented data- bases. A special level-of-detail-aggregation is introduced to handle multiscale representations. Furthermore, a strategy for the smooth integration of subsurface structures is proposed. We have shown how the different aspects of the model can be mapped to GML3. Since the model is based on concepts stan- dardized by the ISO and the OpenGIS Consortium, it consti- tutes a first step towards unified, interoperable 3D city models.

Further investigations have to be done regarding the modeling of appearances and physical characteristics (material, textures). Another issue of future work will be the integration with concepts from the field of computer aided architectural design (CAAD). Here, it has to be examined to what extent the other established approach for 3D modeling, Constructive Solid Geometry (CSG, Foley et al., 1995), can be incorporated into the concept. In addition to a common base model, also common application models are needed to reach semantic interopera- bility, e.g. building a 3D cadastre standard for municipalities. Because objects have both differing thematic and spatial charac- teristics at different scales, the first step would be the definition of discrete scale levels (analogously to the commonly used map scales), in which objects have the same representation. For each level the application specific classes and their substructures, attributes, and relations have to be specified.

We wish to thank the members of the base modeling group of the SIG 3D of the GDI NRW, in particular Rudiger Drees and Hardo Muller, for constructive discussions. Furthermore, we like to thank our colleagues at the Institute for Cartography and Geoinformation, in particular Lutz Plumer and Ingo Petzold. Thanks go to Daniela Schulz and Till Baberg for assistance in preparing the illustrations.

TOWARDS UNIFIED 3D CITY MODELS

Kolbe T. H., Groger G. nstitute for Cartography and Geoinformation, University of Bonn

Kolbe T. H., Groger G.
nstitute for Cartography and Geoinformation, University of Bonn